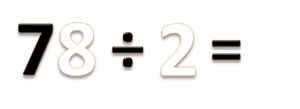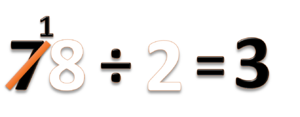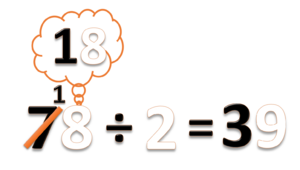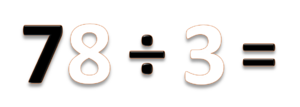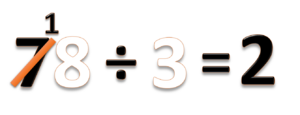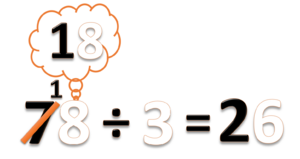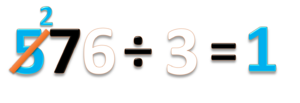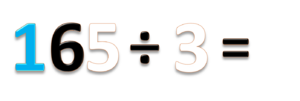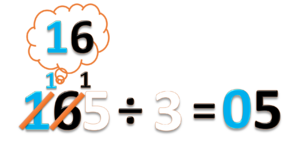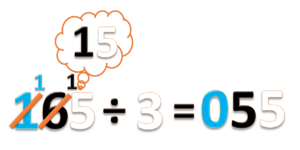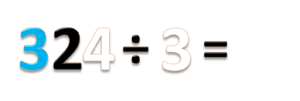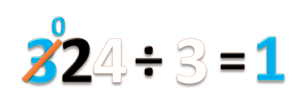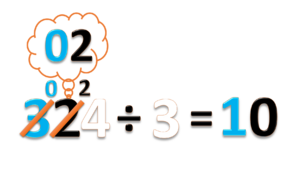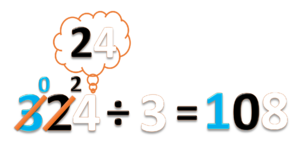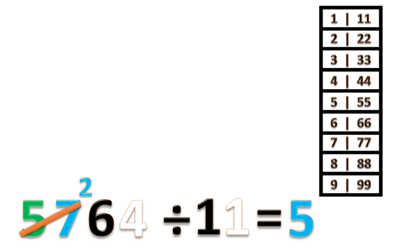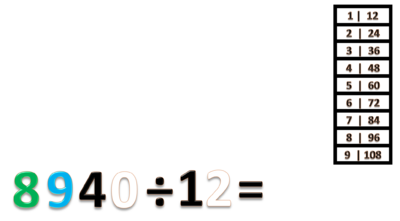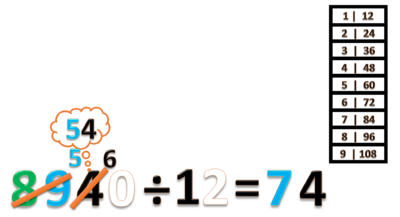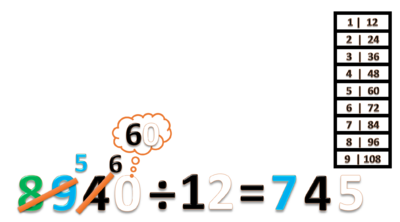Difference between revisions of "GABER Pembagian"
Yohannespkc (talk | contribs) |
Yohannespkc (talk | contribs) |
||
| Line 34: | Line 34: | ||
Cara mendapatkan hasil 6 ÷ 2 | Cara mendapatkan hasil 6 ÷ 2 | ||
Ini ada 6 bola | Ini ada 6 bola | ||
| Line 45: | Line 43: | ||
[[Image:Screen Shot 2022-02-01 at 16.07.43.png|400px]] | [[Image:Screen Shot 2022-02-01 at 16.07.43.png|400px]] | ||
;Langkah 2 | ;Langkah 2 | ||
Revision as of 04:41, 24 September 2023
GASING Berhitung: Pembagian
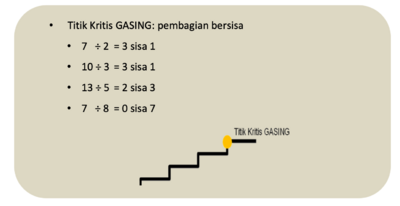
- Titik kritis Gasing Pembagian
- Titik kritis Gasing dalam pembagian adalah kondisi dimana siswa mampu melakukan pembagian bersisa secara mencongak.
Untuk mencapai titik kritis gasing siswa harus melalui tahapan-tahapan sebagai berikut:
- Mengenal arti pembagian
- Pembagian bilangan dengan bilangan 1 angka, hasilnya berupa bilangan 1 angka. Dan Hubungannya dengan perkalian
- Pembagian bersisa.
Konsep Pembagian
- Mengenal Arti Pembagian
- Pembagian adalah proses mendistribusikan atau membagikan habis sejumlah benda kepada sejumlah wadah dimana tiap wadah mendapatkan jumlah benda yang sama.
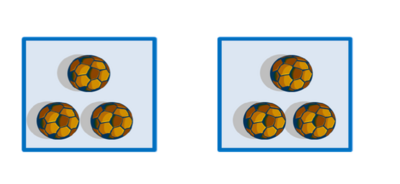
- Misalnya: ada 6 bola hendak dibagikan pada 2 kotak.
- Agar adil tiap kotak menerima 3 bola.
- Kita tuliskan proses ini sebagai 6 ÷ 2 = 3 (dibaca enam dibagi dua sama dengan tiga).
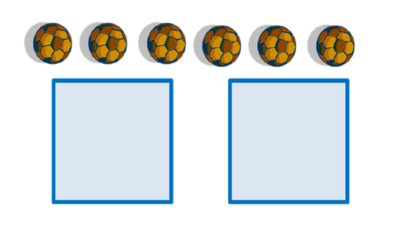
Cara mendapatkan hasil 6 ÷ 2
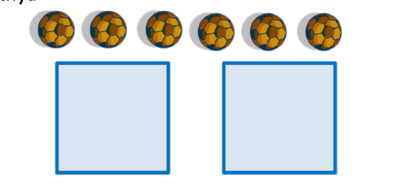
Ini ada 6 bola
- Langkah 1
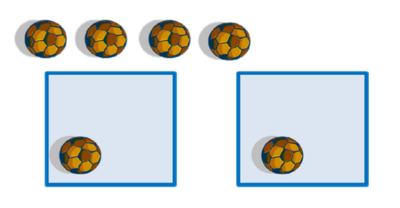
- Bagikan masing-masing 1 bola ke dalam tiap kotak
- Langkah 2
- Bagikan lagi masing-masing 1 bola dalam tiap kotak.
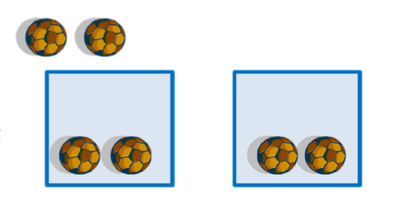
- Langkah 3
- Bagikan lagi masing-masing 1 bola dalam tiap kotak.
- Bola sudah habis dibagikan. Tiap kotak menerima 3 bola.
- Dengan demikian kita katakan bahwa 6 ÷ 2 =3
Catatan: 6 ÷ 2 = dapat diartikan sebagai berapa benda diterima oleh tiap kotak jika 6 benda dibagikan secara adil (merata) pada 2 kotak.
Atau: ada 6 benda hendak dibagikan secara adil dalam 2 kotak, berapa isi masing-masing kotak.
Pembagian bilangan dengan bilangan 1 angka, hasilnya bilangan 1 angka
Pada bagian ini akan dibagi menjadi 2 bagian, yaitu:
- 1. Pembagian bilangan dengan bilangan 1 angka tetapi hasilnya juga 1 angka dan tidak bersisa (habis :dibagi).
- 2. Pembagian bilangan dengan bilangan 1 angka tetapi hasilnya juga 1 angka dan bersisa (tidak habis :dibagi).
- Bagian 1:
- Pembagian bilangan dengan bilangan 1 angka tetapi hasilnya juga 1 angka dan tidak bersisa (habis :dibagi).
KONKRET
- Misalnya kita menghitung nilai dari 6 : 2
Kita lakukan langkah-langkah seperti diatas,
- Arti 6 ÷ 2 = adalah ada 6 benda hendak dimasukan/dibagikan secara adil dalam 2 kotak, berapa isi tiap kotak?
- Arti 2 x ... = 6 adalah ada 2 kotak masing-masing harus di isi berapa benda agar jumlahnya ada 6 benda?
Kalau dipikir kedua kalimat diatas bermakna sama. Yaitu sama-sama menghitung isi kotak.
Karena kita sudah belajar perkalian, maka untuk menghitung cepat pembagian, kita memanfaatkan ilmu perkalian kita.
- Pembagian 9
- Kita ingatkan dulu
- 9 x ... = 9
- 9 x ... = 18
- 9 x ... = 27
- 9 x ... = 36
- 9 x ... = 45
- 9 x ... = 54
- 9 x ... = 63
- 9 x ... = 72
- 9 x ... = 81
- 9 x ... = 90
Kemudian baru kita ajarkan
- 9 ÷ 9 =
- 18 ÷ 9 =
- 27 ÷ 9 =
- 36 ÷ 9 =
- 45 ÷ 9 =
- 54 ÷ 9 =
- 63 ÷ 9 =
- 72 ÷ 9 =
- 81 ÷ 9 =
- 90 ÷ 9 =
- Pembagian 8
- Kita ingatkan dulu
- 8 x ... = 8
- 8 x ... = 16
- 8 x ... = 24
- 8 x ... = 32
- 8 x ... = 40
- 8 x ... = 48
- 8 x ... = 56
- 8 x ... = 64
- 8 x ... = 72
- 8 x ... = 80
Kemudian baru kita ajarkan
- 8 ÷ 8 =
- 16 ÷ 8 =
- 24 ÷ 8 =
- 32 ÷ 8 =
- 40 ÷ 8 =
- 48 ÷ 8 =
- 56 ÷ 8 =
- 64 ÷ 8 =
- 72 ÷ 8 =
- 80 ÷ 8 =
- Pembagian 7
- Kita ingatkan dulu
- 7 x ... = 7
- 7 x ... = 14
- 7 x ... = 21
- 7 x ... = 28
- 7 x ... = 35
- 7 x ... = 42
- 7 x ... = 49
- 7 x ... = 56
- 7 x ... = 63
- 7 x ... = 70
Kemudian baru kita ajarkan
- 7 ÷ 7 =
- 14 ÷ 7 =
- 21 ÷ 7 =
- 28 ÷ 7 =
- 35 ÷ 7 =
- 42 ÷ 7 =
- 49 ÷ 7 =
- 56 ÷ 7 =
- 63 ÷ 7 =
- 70 ÷ 7 =
Lakukan ini untuk perkalian/pembagian 6, 5, 4, 3, 2, dan 1
Aktivitas 1a mencongak
- Siswa dilatih secara cepat mencongak pembagian dengan bilangan 1 angka.
Aktivitas 1b berlatih pembagian dengan bilangan 1 angka
- Tujuan: Siswa menuliskan dengan cepat hasil pembagian dengan bilangan 1 angka
- Siswa mengerjakan dari buku Pengurangan dan Pembagian (buku 3) Latihan 10, 11a-b
Pembagian Bersisa
Kita akan belajar pembagian dengan bilangan 1 angka tetapi ada sisanya.
Untuk mudahnya ini ada 9 kelereng,

Kelereng ini hendak dimasukan dalam 2 kotak. Berapa kelereng yang diterima tiap kotak?
- Kita lihat bahwa tiap kotak menerima 4 kelereng. Tapi masih ada sisa 1.
- Kita tuliskan 9 ÷ 2 = 4 sisa 1 (dibaca Sembilan dibagi dua adalah 4 sisa 1)
- Selanjutnya kita minta siswa melakukan eksplorasi dengan menggunakan kelereng dan melakukan pembagian 2
- 3 ÷ 2 =
- 5 ÷ 2 =
- 7 ÷ 2 =
- 9 ÷ 2 =
- 11 ÷ 2 =
- 13 ÷ 2 =
- 15 ÷ 2 =
- 17 ÷ 2 =
- Kemudian minta siswa menyimpulkan bagaimana cara cepat untuk menghitung pembagian bersisa ini?
- Cara cepatnya adalah dengan mencari bilangan apa yang kalau dikalikan dengan bilangan pembagi hasilnya lebih kecil dan paling dekat dengan bilangan yang dibagi.
- Misalnya 17 ÷ 2 = , untuk menjawab ini kita mencari bilangan apa yang dikalikan 2 hasilnya lebih kecil dan paling dekat dengan 17.
- Kita coba 6 x 2 = 12, terlalu jauh dari 17
- Coba 7 x 2 = 14, sudah lebih dekat ke 17
- Coba 8 x 2 = 16, Lebih dekat ke 17
- Coba 9 x 2 = 18, terlalu besar, melebihi 17.
- Jawabnya 17 ÷ 2 = 8, untuk mencari sisanya kita kurangkan 17 dengan 16 (bilangan terdekat dengan 17 dan bisa habis dibagi 2) yaitu 17 - 16 = 1
- Jadi 17 ÷ 2 = 8 sisa 1
Latih ini berulang-ulang. Setelah mahir dengan perbagian 2, masuk ke pembagian 10.
- 46 ÷ 10 = ...
- Siswa mencari bilangan apa yang dikalikan 10 mendekati 46
- coba 3 x 10 = 30 masih jauh dari 46
- coba 4 x 10 = 40 sudah dekat 46
- coba 5 x 10 = 50 lebih dari 46
- Jawabnya 46 ÷ 10 = 4 dengan sisa 6. Sisa diperoleh dari 46 dikurangi bilangan yang lebih kecil dan paling dekat 46. Sisa = 46 - 40 = 6
- Jadi 46 ÷ 10 = 4 sisa 6
Kita bisa memberikan soal-soal berikut secara mencongak
- 57 ÷ 10 =
- 36 ÷ 10 =
- 81 ÷ 10 =
- 92 ÷ 10 =
- 45 ÷ 10 =
- 68 ÷ 10 =
- dst...
Setelah itu pembagian bersisa yang agak mudah adalah pembagian 5
- Kita latih seperti pembagian 10 diatas
- 17 ÷ 5 =
- 12 ÷ 5 =
- 23 ÷ 5 =
- 27 ÷ 5 =
- 36 ÷ 5 =
- 48 ÷ 5 =
- dst...
- Setelah itu bisa ke berbagai jenis perkalian. Boleh secara acak jika siswanya sudah mahir perkalian. Tapi boleh juga secara berurut 3, 4, 6, 7, 8 dan 9.
- Usahakan anak-anak mahir dalam mencongak pembagian bersisa ini.
Aktivitas 2 berlatih pembagian bersisa
- Tujuan: Siswa menuliskan dengan cepat hasil pembagian bersisa
- Siswa mengerjakan dari buku Pengurangan dan Pembagian (buku 3) Latihan 13a-c
Video ini menunjukan bagaimana anak-anak dapat mencongak pembagian dengan bilangan 1 angka.
{{#ev:youtube|zclncyxtBS4 |width=900 |height=500 |||start=10&end=120 }}
Pembagian sebarang bilangan dengan bilangan 1 angka
Dengan menguasai pembagian bersisa maka pembagian suatu bilangan dengan bilangan 1 angka ini sangat mudah.
Mari kita lihat beberapa contoh
- a) 78 ÷ 2 =
- Bilangan 78 terdiri dari 7 puluhan dan 8 satuan
- Bagi puluhannya, 7 ÷ 2 = 3 sisa 1
- Tulis hasil baginya 3 (angka 3 ini artinya 3 puluhan)
- Sisanya 1 puluhan
- Tulis sisanya. di antara angka 7 dan 8
- Jangan lupa coret angka 7 (sebagai tanda bahwa kita sudah menyelesaikan pembagian 7 puluhan ini).
- Sekarang kita punya sisa 1 puluhan
- Kita juga punya 8 satuan.
- 1 Puluhan + 8 satuan = 18 satuan.
- Hasilnya ini bagi dengan 2.
- 18 ÷ 2 = 9
- Tulis hasilnya 9 pada nilai tempat satuan
- Jangan lupa coret tangka 8 sebagai tanda bahwa 8 satuan ini juga sudah selesai dibagi).
- Jadi 78 ÷ 2 = 39
- b) 78 ÷ 3 =
- Bilangan 78 terdiri dari 7 puluhan dan 8 satuan
- Bagi puluhannya, 7 ÷ 3 = 2 sisa 1
- Tulis hasil baginya 2 (angka 2 ini artinya 2 puluhan)
- Tulis sisanya diantara angka 7 dan 8.
- Jangan lupa coret angka 7 (sebagai tanda bahwa kita sudah menyelesaikan pembagian 7 puluhan ini).
- Sekarang kita punya sisa 1 puluhan
- Kita juga punya 8 satuan.
- Gabungkan ini menjadi 18 satuan. Lalu bagi dengan 3.
- 18 ÷ 3 = 6
- Tulis hasilnya 6 pada nilai tempat satuan
- Jangan lupa coret tangka 8 sebagai tanda bahwa 8 satuan ini juga sudah selesai dibagi).
- Jadi 78 ÷ 3 = 26
- c) 576 ÷ 3 =
- Bilangan 576 terdiri dari 5 ratusan (biru) 7 puluhan (hitam) dan 6 satuan (putih)
- Bagi ratusannya, 5 ÷ 3 = 1 sisa 2
- Tulis hasil baginya 1.
- Tulis sisanya 2 diantara angka 5 dan 7
- Coret angka 5.
- Sekarang kita punya sisa 2 ratusan
- Kita juga punya 7 puluhan
- Gabungkan ini menjadi 27 puluhan. Lalu bagi dengan 3.
- 27 ÷ 3 = 9 sisa 0.
- Tulis hasilnya 9 pada nilai tempat puluhan
- tulis sisanya 0, diantara angka 7 dan 6
- Jangan lupa coret angka 7
- Kita punya sisa 0 puluhan
- Kita juga punya 6 satuan.
- Gabungkan ini menjadi 06 satuan atau 6 satuan. Lalu bagi dengan 3.
- 6 ÷ 3 = 2
- Tulis hasilnya 2 pada nilai tempat satuan
- Jangan lupa coret angka 6
- Jadi 576 ÷ 3 = 192
- d) 165 ÷ 3 =
- Bilangan 165 terdiri dari 1 ratusan (biru) 6 puluhan (hitam) dan 5 satuan (putih)
- Bagi ratusannya, 1 ÷ 3 = 0 sisa 1
- Tulis hasil baginya 0.
- Tulis sisanya 1 diantara angka 1 dan 6.
- Jangan lupa coret angka 1.
- Sekarang kita punya sisa 1 ratusan
- Kita juga punya 6 puluhan
- Gabungkan ini menjadi 16 puluhan. Lalu bagi dengan 3.
- 16 ÷ 3 = 5 sisa 1.
- Tulis hasilnya 5 pada nilai tempat puluhan
- tulis sisanya 1, diantara angka 6 dan 5
- Jangan lupa coret angka 6.
- Kita punya sisa 1 puluhan
- Kita juga punya 5 satuan.
- Gabungkan ini menjadi 15 satuan. Lalu bagi dengan 3.
- 15 ÷ 3 = 5
- Tulis hasilnya 5 pada nilai tempat satuan
- Jangan lupa coret angka 5.
- Jadi 165 ÷ 3 = 055 atau 55
- e) 324 ÷ 3 =
- Bilangan 324 terdiri dari 3 ratusan (biru) 2 puluhan (hitam) dan 4 satuan (putih)
- Bagi ratusannya, 3 ÷ 3 = 1 sisa 0
- Tulis hasil baginya 1.
- Tulis sisanya 0. di antara angka 3 dan 2.
- Jangan lupa coret angka 3.
- Sekarang kita punya sisa 0 ratusan
- Kita juga punya 2 puluhan
- Gabungkan ini menjadi 02 puluhan atau 2 puluhan. Lalu bagi dengan 3.
- 2 ÷ 3 = 0 sisa 2.
- Tulis hasilnya 0 pada nilai tempat puluhan
- tulis sisanya 2, diantara angka 2 dan 4.
- Jangan lupa coret angka 2.
- Kita punya sisa 2 puluhan
- Kita juga punya 4 satuan.
- Gabungkan ini menjadi 24 satuan. Lalu bagi dengan 3.
- 24 ÷ 3 = 8
- Tulis hasilnya 8 pada nilai tempat satuan
- Jangan lupa coret angka 4.
- Jadi 324 ÷ 3 = 108
- f) bagaimana 1200 ÷ 4 = ?
- Untuk bilangan yang diikuti dengan banyak nol, cara pembagiannya adalah kita lakukan pembagian untuk bilangan yang bukan nol.
- Kemudian kita tambahkan nol dibelakangnya.
- Untuk 1200 ÷ 4 =
- 12 ÷ 4 = 3
- Dibelakang 12 ada dua nol. Maka hasilnya ada 3 diikuti dengan 2 nol dibelakangnya yaitu 300
- Jadi 1200 ÷ 4 = 300
- Kita bisa membuktikan juga ini dengan menggunakan cara a sampai e diatas.
Untuk beberapa contoh pembagian dengan bilangan 1 angka dapat dilihat di video berikut
{{#ev:YouTube
|id=jEJywjpVOck
|width=900
|height=500
}}
Aktivitas 3 berlatih pembagian dengan bilangan 1 angka
- Tujuan: Siswa menuliskan dengan cepat hasil pembagian dengan bilangan 1 angka
- Siswa mengerjakan dari buku Pengurangan dan Pembagian (buku 3) Latihan 12 dan 14a-c
Pembagian dengan bilangan 2 angka
Konsep pembagian dengan bilangan 2 angka hampir sama seperti pembagian dengan bilangan 1 angka.
Untuk jelasnya mari kita lihat contoh berikut
- a) 5764 ÷ 11 = ...
- Langkah pertama adalah kita membuat tabel perkalian 11
Cara membuatnya adalah dengan melakukan penjumlahan berulang:
- 11
- 11 + 11 = 22
- 22 + 11 = 33
- 33 + 11 = 44
- 44 + 11 = 55
- 55 + 11 = 66
- 66 + 11 = 77
- 77 + 11 = 88
- 88 + 11 = 99
- Bagi ribuannya, 5 ÷ 11 = 0 sisa 5
- Kita boleh juga ambil ribuan dan ratusan sekaligus (hanya untuk pembagian pertama saja)
- untuk itu ubah 5 ribuan jadi 50 ratusan
- Jadi disini kita punya 57 ratusannya
- Bagi ratusannya 57 : 11 = 5 sisa 2 (gunakan tabel perkalian 11)
- Tulis hasil baginya 5 (angka 5 ini adalah mempunyai nilai tempat ratusan)
- Tulis sisanya 2. di antara angka 7 dan 6
- Jangan lupa coret angka 5 dan 7
- Sekarang kita punya sisa 2 ratusan
- Kita juga punya 6 puluhan
- Gabungkan ini menjadi 26 puluhan. Lalu bagi dengan 11.
- 26 ÷ 11 = 2 sisa 4 (gunakan tabel perkalian 11)
- Tulis hasilnya 2 pada nilai tempat puluhan
- tulis sisanya 4, diantara angka 6 dan 4
- Jangan lupa coret angka 6
- Kita punya sisa 4 puluhan
- Kita juga punya 4 satuan.
- Gabungkan ini menjadi 44 satuan. Lalu bagi dengan 11.
- 44 ÷ 11 = 4 (gunakan tabel perkalian 11).
- Tulis hasilnya 4 pada nilai tempat satuan
- Jangan lupa coret angka 4
- Jadi 5764 ÷ 11 = 524
Berikan banyak contoh pembagian dengan 11 ini. Ini bisa dilakukan tanpa membuat table perkalian 11 karena perkalian 11 ini mudah.
- b) 8940 ÷ 12 = ...
- Langkah pertama adalah kita membuat table perkalian 12
Caranya adalah dengan melakukan penjumlahan berulang
- 12
- 12 + 12 = 24
- 24 + 12 = 36
- 36 + 12 + 48
- 48 + 12 = 60
- 60 + 12 = 72
- 72 + 12 = 84
- 84 + 12 = 96
- 96 + 12 = 108
- Kita ambil 2 angka pertama 89
- Ubah 8 ribuan jadi 80 ratusan
- Jadi kita punya 80 ratusan + 9 ratusan = 89 ratusan
- Bagi ratusannya 89 : 12 = 7 sisa 5 (gunakan tabel perkalian 12)
- Tulis hasil baginya 7.
- Tulis sisanya 5. Diantara angka 9 dan 4
- Jangan lupa coret angka 8 dan 9.
- Sekarang kita punya sisa 5 ratusan
- Kita juga punya 4 puluhan
- Gabungkan ini menjadi 54 puluhan. Lalu bagi dengan 12.
- 54 ÷ 12 = 4 sisa 6 (gunakan tabel perkalian 12)
- Tulis hasilnya 4 pada nilai tempat puluhan
- tulis sisanya 6, diantara angka 4 dan 0.
- Jangan lupa coret angka 4
- Kita punya sisa 6 puluhan
- Kita juga punya 0 satuan.
- Gabungkan ini menjadi 60 satuan. Lalu bagi dengan 12.
- 60 ÷ 12 = 5 (gunakan tabel perkalian 12).
- Tulis hasilnya 5 pada nilai tempat satuan
- Jangan lupa coret angka 0.
- Jadi 8940 ÷ 12 = 745
Untuk pembagian dengan bilangan 2 angka dapat dilihat contohnya di video berikut
{{#ev:youtube|lb3p1LjYAxg |width=900 |height=500 |||start=10&end=120 }}
Pembagian dengan bilangan 3 angka atau lebih bisa dilakukan dengan cara yang sama yaitu dengan membuat tabel perkalian dulu.
Aktivitas 4 berlatih pembagian dengan bilangan 2 angka
- Tujuan: Siswa menuliskan dengan cepat hasil pembagian dengan bilangan 2 angka
- Siswa mengerjakan dari buku Pengurangan dan Pembagian (buku 3) Latihan 15 dan 16