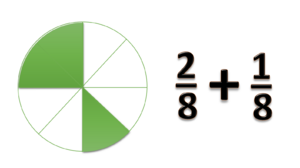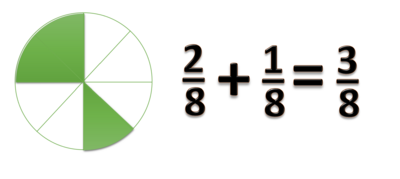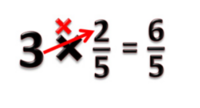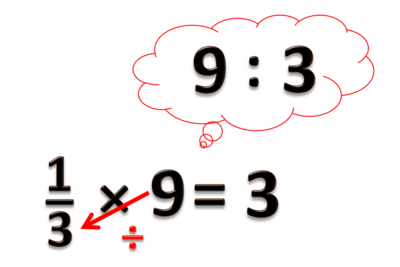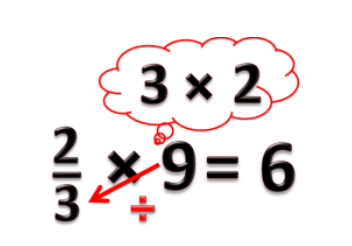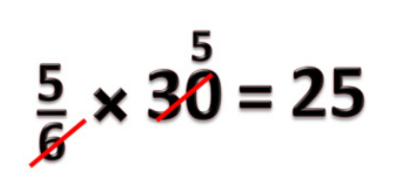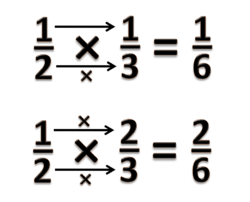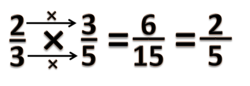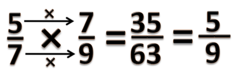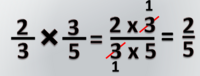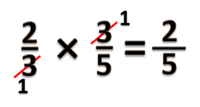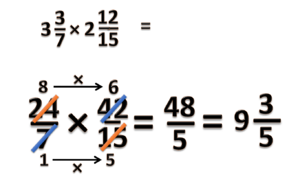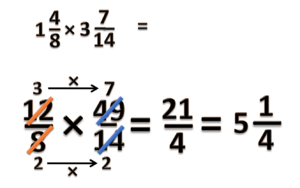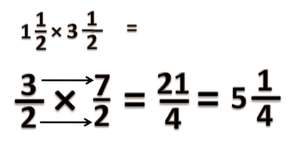Difference between revisions of "GABER Pecahan"
Yohannespkc (talk | contribs) m (→Penjumlahan) |
Yohannespkc (talk | contribs) |
||
| (27 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
= Gasing Berhitung: Pecahan = | = Gasing Berhitung: Pecahan = | ||
| Line 258: | Line 257: | ||
Gambar ini adalah pecahan <small><math>\frac{2}{8} </math></small> | Gambar ini adalah pecahan <small><math>\frac{2}{8}</math></small> | ||
:: [[Image:Screen Shot 2022-02-19 at 05.38.11.png|200px]] | |||
:: <small><math>\frac{2}{8}</math></small> menunjukan nilai 2 bagian dari suatu kelompok yang terdiri dari 8 bagian yang sama nilainya | |||
:: Kemudian kita tambahkan <small><math>\frac{2}{8}</math></small> | |||
:: <small><math>\frac{ | :: Kemudian kita tambahkan <small><math>\frac{1}{8}</math></small> | ||
[[Image:Screen Shot 2022-02-19 at 05.38.22.png|300px]] | :: [[Image:Screen Shot 2022-02-19 at 05.38.22.png|300px]] | ||
Hasilnya dengan mudah terlihat | :: Hasilnya dengan mudah terlihat <small><math>\frac{3}{8}</math></small> | ||
[[Image:Screen Shot 2022-02-19 at 05.38.32.png|400px]] | :: [[Image:Screen Shot 2022-02-19 at 05.38.32.png|400px]] | ||
:: <small><math>\frac{3}{8} </math></small> menunjukan 3 bagian dari suatu kelompok yang terdiri dari 8 bagian yang sama nilainya. | :: <small><math>\frac{3}{8}</math></small> menunjukan 3 bagian dari suatu kelompok yang terdiri dari 8 bagian yang sama nilainya. | ||
Contoh lain: | Contoh lain: | ||
| Line 350: | Line 353: | ||
Mengerjakan Latihan 14 dari buku Pecahan (buku 4) | Mengerjakan Latihan 14 dari buku Pecahan (buku 4) | ||
== | == Konsep SATU == | ||
Ini 1 jeruk, kita potong menjadi 2 bagian yang sama besar. | |||
[[Image:Screen Shot 2022-02-19 at 06.55.46.png|300px]] | [[Image:Screen Shot 2022-02-19 at 06.55.46.png|300px]] | ||
Satu bagian jeruk ini nilainya adalah <small><math>\frac{1}{2} </math></small> jeruk. | |||
Karena | Karena itu maka | ||
:: <small><math>\frac{1}{2} </math></small> (jeruk) + <small><math>\frac{1}{2} </math></small> (jeruk) = 1 (jeruk) | :: <small><math>\frac{1}{2} </math></small> (jeruk) + <small><math>\frac{1}{2} </math></small> (jeruk) = 1 (jeruk) | ||
Atau kita hilangkan konteksnya, kita peroleh | |||
:: <small><math>\frac{1}{2} </math></small> + <small><math>\frac{1}{2} </math></small> = 1 | :: <small><math>\frac{1}{2} </math></small> + <small><math>\frac{1}{2} </math></small> = 1 | ||
| Line 381: | Line 381: | ||
Contoh lain | Contoh lain | ||
Kita punya 1 batang kuning, kemudian batang itu kita potong menjadi 4 bagian yang sama nilainya. | |||
:Berapa seperempat batang kuning ditambah seperempat batang kuning ditambah seperempat batang kuning ditambah seperempat batang kuning ? | :Berapa seperempat batang kuning ditambah seperempat batang kuning ditambah seperempat batang kuning ditambah seperempat batang kuning ? | ||
| Line 408: | Line 410: | ||
Jadi bisa disimpulkan bahwa dalam | Jadi bisa disimpulkan bahwa dalam pecahan arti bilangan 1 adalah sebagai berikut | ||
:: 1 adalah nilai 2 bagian dari satu kelompok yang terdiri dari 2 bagian yang sama | :: 1 adalah nilai 2 bagian dari satu kelompok yang terdiri dari 2 bagian yang sama nilainya. | ||
:: 1 adalah nilai 3 bagian dari satu kelompok yang terdiri dari 3 bagian yang sama | :: 1 adalah nilai 3 bagian dari satu kelompok yang terdiri dari 3 bagian yang sama nilainya. | ||
:: 1 adalah nilai 5 bagian dari satu kelompok yang terdiri dari 5 bagian yang sama | :: 1 adalah nilai 5 bagian dari satu kelompok yang terdiri dari 5 bagian yang sama nilainya. | ||
Video berikut ini menjelaskan konsep <nowiki>"satu'</nowiki> | Video berikut ini menjelaskan konsep <nowiki>"satu'</nowiki> | ||
| Line 429: | Line 431: | ||
Mengerjakan Latihan 5 dari buku Pecahan (buku 4) | Mengerjakan Latihan 5 dari buku Pecahan (buku 4) | ||
== Pecahan adalah Bagi == | |||
:Apakah pecahan itu adalah bagi? | |||
:Apakah <small><math>\frac{1}{2} </math></small> = 1 ÷ 2 ? | :Apakah <small><math>\frac{1}{2} </math></small> = 1 ÷ 2 ? | ||
| Line 454: | Line 452: | ||
Menurut definisi pecahan, | Menurut definisi pecahan, | ||
:: separuh atau setengah kue | :: separuh atau setengah kue menunjukan nilai 1 bagian dari satu kue yang terdiri dari dua bagian yang sama nilainya. | ||
:: Ini ditulis <small><math>\frac{1}{2} </math></small> kue | :: Ini ditulis <small><math>\frac{1}{2} </math></small> kue | ||
| Line 513: | Line 511: | ||
Mengerjakan Latihan 7 dari buku Pecahan (buku 4) | Mengerjakan Latihan 7 dari buku Pecahan (buku 4) | ||
== | == Pecahan Majemuk == | ||
Berapa <small><math>\frac{2}{3}</math></small> + <small><math>\frac{2}{3}</math></small>? | Berapa <small><math>\frac{2}{3}</math></small> + <small><math>\frac{2}{3}</math></small>? | ||
| Line 541: | Line 539: | ||
::<small><math>\frac{25}{23}</math></small> = <small><math>\frac{23}{23}</math></small> + <small><math>\frac{2}{23}</math></small> = 1<small><math>\frac{2}{23}</math></small> | ::<small><math>\frac{25}{23}</math></small> = <small><math>\frac{23}{23}</math></small> + <small><math>\frac{2}{23}</math></small> = 1<small><math>\frac{2}{23}</math></small> | ||
::<small><math>\frac{7}{2}</math></small> = <small><math>\frac{6}{2}</math></small> + <small><math>\frac{1}{2}</math></small> = 3<small><math>\frac{1}{2}</math></small> | |||
::<small><math>\frac{11}{3}</math></small> = <small><math>\frac{9}{3}</math></small> + <small><math>\frac{2}{3}</math></small> = 3<small><math>\frac{2}{3}</math></small> | |||
| Line 561: | Line 565: | ||
Mengerjakan Latihan 6 dari buku Pecahan (buku 4) | Mengerjakan Latihan 6 dari buku Pecahan (buku 4) | ||
== | == Penjumlahan dan Pengurangan dengan Penyebut berbeda == | ||
Pada bagian ini kita akan melakukan operasi penjumlahan dan pengurangan dengan penyebut berbeda. | Pada bagian ini kita akan melakukan operasi penjumlahan dan pengurangan dengan penyebut berbeda. | ||
=== | === Penjumlahan Pecahan === | ||
| Line 574: | Line 578: | ||
:: Kita harus ubah penyebutnya sehingga sama. | :: Kita harus ubah penyebutnya sehingga sama. | ||
Bagaimana caranya? | |||
Kita lihat konkretnya dulu | |||
Ini ada batang <small><math>\frac{1}{2}</math></small> hendak ditambahkan dengan batang <small><math>\frac{1}{3}</math></small>. | |||
: | [[Image: Screenshot_2023-12-28_at_08.39.51.png|400px]] | ||
Agar kedua batang ini bisa dijumlahkan maka kelompoknya harus disamakan. | |||
Cara | Cara menyamakan kelompok adalah sebagai berikut: | ||
: | |||
Pada pecahan <small><math>\frac{1}{2}</math></small>, tiap bagian kita potong menjadi 3 bagian yang identik. Sehingga kelompoknya menjadi kelompok 6. | |||
Pada pecahan <small><math>\frac{1}{3}</math></small>, tiap bagian kita potong menjadi 2 bagian yang identik. Sehingga kelompoknya menjadi kelompok 6. | |||
Nah sekarang kedua pecahan mempunyai kelompok yang sama. | |||
[[Image: Screenshot 2023-12-28 at 08.46.27.png|400px]] | |||
Secara abstrak ini dituliskan | |||
:: <small><math>\frac{1}{2}</math></small> dijadikan <small><math>\frac{3}{6}</math></small> | |||
:: <small><math>\frac{1}{3}</math></small> dijadikan <small><math>\frac{2}{6}</math></small> | |||
Sehingga kita peroleh | |||
:: <small><math>\frac{1}{ | :: <small><math>\frac{1}{2}</math></small> + <small><math>\frac{1}{3}</math></small> = <small><math>\frac{3}{6}</math></small> + <small><math>\frac{2}{6}</math></small> = <small><math>\frac{5}{6}</math></small> | ||
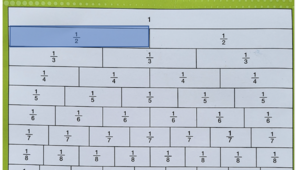
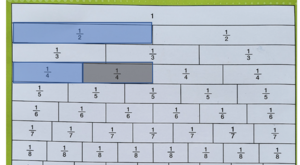
Cara lain adalah menggunakan | Cara Konkret lain adalah menggunakan Papan pecahan. | ||
:: Misal kita akan menghitung <small><math>\frac{1}{2}</math></small> + <small><math>\frac{1}{3}</math></small> = | :: Misal kita akan menghitung <small><math>\frac{1}{2}</math></small> + <small><math>\frac{1}{3}</math></small> = | ||
Ini adalah | Ini adalah Papan pecahan. | ||
[[Image:Screen Shot 2022-02-22 at 11.14.18.png|400px]] | [[Image:Screen Shot 2022-02-22 at 11.14.18.png|400px]] | ||
| Line 662: | Line 641: | ||
Cara lain (abstrak) mendapat penyebut 6 untuk soal di atas. | |||
Cara termudah adalah | |||
:: Mengalikan penyebut pecahan yang dijumlahkan yaitu 3 x 2 | |||
Cara lain: | |||
:: Dengan mencari bilangan terkecil yang bisa dibagi 2 dan bisa dibagi 3. | |||
Apakah penyebutnya boleh 12? Bukankah 12 juga bisa dibagi 2 atau dibagi 3? | |||
::Boleh namun hasilnya nanti kamu harus sederhanakan lagi | |||
::<small><math>\frac{1}{2}</math></small> + <small><math>\frac{1}{3}</math></small> = <small><math>\frac{6}{12}</math></small> + <small><math>\frac{4}{12}</math></small> = <small><math>\frac{10}{12}</math></small> = <small><math>\frac{5}{6}</math></small> | |||
Kita boleh mengubah pecahan menjadi 6, 12, 18, 24 dsb. Tetapi sebaiknya ambil yang terkecil yaitu 6. | |||
== | Bagaimana menghitung <small><math>\frac{1}{4}</math></small> + <small><math>\frac{1}{6}</math></small> = ? | ||
:: Kita ubah penyebutnya menjadi 4 x 6 = 24 | |||
:: <small><math>\frac{1}{4}</math></small> + <small><math>\frac{1}{6}</math></small> = <small><math>\frac{6}{24}</math></small> + <small><math>\frac{4}{24}</math></small> = <small><math>\frac{10}{24}</math></small> = <small><math>\frac{5}{12}</math></small> | |||
Atau | |||
:: cari bilangan yang bisa dibagi 4 dan 6. Dalam hal ini bilangannya adalah 12, 24, 36 dsb. | |||
:: Kita pilih bilangan yang terkecil yaitu 12. | |||
<math> | :: <small><math>\frac{1}{4}</math></small> + <small><math>\frac{1}{6}</math></small> = <small><math>\frac{3}{12}</math></small> + <small><math>\frac{2}{12}</math></small> = <small><math>\frac{5}{12}</math></small> | ||
\frac{ | |||
</math> | |||
Bagaimana dengan <small><math>\frac{2}{5}</math></small> + <small><math>\frac{3}{10}</math></small> = ? | |||
:: kita ubah penyebutnya menjadi 5 x 10 = 50 | |||
: | :: <small><math>\frac{2}{5}</math></small> + <small><math>\frac{3}{10}</math></small> = <small><math>\frac{20}{50}</math></small> + <small><math>\frac{15}{50}</math></small> = <small><math>\frac{35}{50}</math></small> = <small><math>\frac{7}{10}</math></small> | ||
Atau | |||
:: Cari bilangan yang bisa dibagi 5 dan bisa dibagi 10. Dalam hal ini bilangannya adalah 10, 20, 30, 40 dst.. | |||
:: Kita pilih bilangan yang terkecil yaitu 10 | |||
<math> | :: <small><math>\frac{2}{5}</math></small> + <small><math>\frac{3}{10}</math></small> = <small><math>\frac{4}{10}</math></small> + <small><math>\frac{3}{10}</math></small> = <small><math>\frac{7}{10}</math></small> | ||
\frac{ | |||
</math> | Berikut ini adalah beberapa contoh penjumlahan pecahan | ||
{{#ev:YouTube | |||
|id= 1iqMwdBkLf8 | |||
|width=640 | |||
|height=400 | |||
}} | |||
1 | |||
=== Penjumlahan cepat === | |||
Perhatikan <small><math>\frac{2}{5}</math></small> + <small><math>\frac{3}{10}</math></small> = | |||
Penyebutnya dijadikan 5 x 10 | |||
<math> | <math> | ||
\begin{array}{lcl} | \begin{array}{lcl} | ||
\frac{ | \frac{2}{5} + \frac{3}{10} & = & \frac{2 \times 10}{5 \times 10} + \frac{3 \times 5}{10 \times 5} \\ | ||
& = & \frac{ | & = & \frac{20}{50} + \frac{15}{50} \\ | ||
& = & \frac{35}{50} \\ | |||
& = & \frac{7}{10} | |||
\end{array} | \end{array} | ||
</math> | </math> | ||
:Penyebutnya dijadikan 3 | Lihat beberapa contoh berikut | ||
a) <small><math>\frac{4}{5}</math></small> + <small><math>\frac{2}{3}</math></small> = | |||
:Penyebutnya dijadikan 5 x 3 | |||
<math> | <math> | ||
\begin{array}{lcl} | \begin{array}{lcl} | ||
\frac{ | \frac{4}{5} + \frac{2}{3} & = & \frac{4 \times 3}{5 \times 3} + \frac{2 \times 5}{3 \times 5} \\ | ||
& = & \frac{ | & = & \frac{12}{15} + \frac{10}{15} \\ | ||
& = & \frac{22}{15} \\ | |||
& = &1 \frac{7}{15} | |||
\end{array} | \end{array} | ||
</math> | </math> | ||
b) <small><math>\frac{1}{2}</math></small> + <small><math>\frac{3}{4}</math></small> = | |||
:Penyebutnya dijadikan | :Penyebutnya dijadikan 2 x 4 | ||
<math> | <math> | ||
\begin{array}{lcl} | \begin{array}{lcl} | ||
\frac{ | \frac{1}{2} + \frac{3}{4} & = & \frac{1 \times 4}{2 \times 4} + \frac{3 \times 2}{4 \times 2} \\ | ||
& = & \frac{ | & = & \frac{4}{8 } + \frac{6}{8 } \\ | ||
& = & \frac{10}{8} \\ | |||
& = & \frac{5}{4} \\ | |||
& = & 1\frac{1}{4} | |||
\end{array} | \end{array} | ||
</math> | </math> | ||
c) <small><math>\frac{1}{3}</math></small> + <small><math>\frac{3}{5}</math></small> = | |||
:Penyebutnya dijadikan 3 x 5 | |||
<math> | |||
\begin{array}{lcl} | |||
\frac{1}{3} + \frac{3}{5} & = & \frac{1 \times 5}{3 \times 5} + \frac{3 \times 3}{5 \times 3} \\ | |||
& = & \frac{5}{15} +\frac{9}{15} \\ | |||
& = & \frac{14}{15} | |||
\end{array} | |||
</math> | |||
d) <small><math>\frac{2}{5}</math></small> + <small><math>\frac{3}{7}</math></small> = | |||
:Penyebutnya dijadikan 5 x 7 | |||
<math> | |||
\begin{array}{lcl} | |||
\frac{2}{5} + \frac{3}{7} & = & \frac{2 \times 7}{5 \times 7} + \frac{3 \times 5}{7 \times 5} \\ | |||
& = & \frac{14}{35} +\frac{15}{35} \\ | |||
& = & \frac{29}{35} | |||
\end{array} | |||
</math> | |||
Ada cara yang dilakukan orang untuk mempercepat perhitungan yaitu dengan pola perkalian silang. Namun di Gasing kami tidak terlalu merekomendasikan cara ini. Karena anak jadi kehilangan konsep menjumlah atau mengurangi pecahan. Yang diingat adalah rumus. | |||
[[Image:Screen Shot 2022-02-21 at 11.45.36.png|250px]] | |||
| Line 772: | Line 800: | ||
=== | === Pengurangan Pecahan === | ||
Pengurangan pecahan dengan penyebut berbeda sama konsepnya dengan penjumlahan pecahan dengan penyebut berbeda. | Pengurangan pecahan dengan penyebut berbeda sama konsepnya dengan penjumlahan pecahan dengan penyebut berbeda. | ||
Mereka yang sudah mahir penjumlahan pecahan akan sangat cepat mengerti pengurangan pecahan ini. | |||
Misalnya bagaimana menghitung <small><math>\frac{1}{4}</math></small> - <small><math>\frac{1}{6}</math></small> = ? | Misalnya bagaimana menghitung <small><math>\frac{1}{4}</math></small> - <small><math>\frac{1}{6}</math></small> = ? | ||
| Line 814: | Line 843: | ||
=== | === Pengurangan cara cepat === | ||
Pola pengurangan pecahan cara cepat sama dengan pola penjumlahan pecahan cara cepat. | Pola pengurangan pecahan cara cepat sama dengan pola penjumlahan pecahan cara cepat. | ||
| Line 824: | Line 853: | ||
<math> | <math> | ||
\begin{array}{lcl} | \begin{array}{lcl} | ||
\frac{2}{5} - \frac{3}{10} & = & \frac{2 \times 10}{5 \times 10} - \frac{ | \frac{2}{5} - \frac{3}{10} & = & \frac{2 \times 10}{5 \times 10} - \frac{3 \times 5}{10 \times 5} \\ | ||
& = & \frac{20}{50} -\frac{15}{50} \\ | |||
& = & \frac{5}{50} \\ | |||
& = & \frac{1}{10} | |||
\end{array} | \end{array} | ||
</math> | </math> | ||
| Line 837: | Line 868: | ||
<math> | <math> | ||
\begin{array}{lcl} | \begin{array}{lcl} | ||
\frac{4}{5} - \frac{3}{7} & = & \frac{4 \times 7}{5 \times 7} - \frac{ | \frac{4}{5} - \frac{3}{7} & = & \frac{4 \times 7}{5 \times 7} - \frac{3 \times 5}{7 \times 5} \\ | ||
& = & \frac{28}{35} -\frac{15}{35} \\ | |||
& = & \frac{13}{35} | |||
\end{array} | \end{array} | ||
</math> | </math> | ||
Lihat video berikut ini untuk beberapa contoh pengurangan cara cepat | Lihat video berikut ini untuk beberapa contoh pengurangan cara cepat | ||
| Line 868: | Line 896: | ||
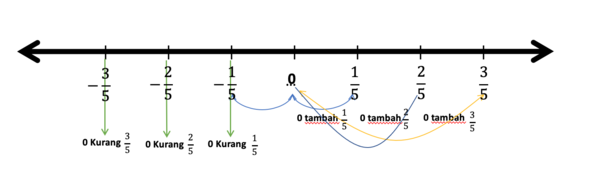
=== | === Pecahan Negatif (cara cepat) === | ||
Konsep pecahan negatif, mirip dengan konsep bilangan bulat negatif. | Konsep pecahan negatif, mirip dengan konsep bilangan bulat negatif. | ||
| Line 881: | Line 909: | ||
Dari titik 0 ke kiri, nilai tiap titik berturut-turut adalah <small><math>-\frac{1}{5}, -\frac{2}{5}, -\frac{3}{5} </math></small> dst. | Dari titik 0 ke kiri, nilai tiap titik berturut-turut adalah <small><math>-\frac{1}{5}, -\frac{2}{5}, -\frac{3}{5} </math></small> dst. | ||
Operasi penjumlahan dan pengurangan bilangan pecahan negatif, adalah seperti operasi bilangan bulat negatif. | |||
Berikut ini adalah beberapa contoh operasi bilangan pecahan negatif. | |||
<small><math>-\frac{ | |||
a) <small><math>-\frac{4}{5}</math></small> + <small><math>\frac{3}{7}</math></small> = | |||
:Penyebutnya dijadikan 5 x 7 | |||
<math> | |||
<math> | |||
\begin{array}{lcl} | \begin{array}{lcl} | ||
-\frac{4}{5} + \frac{3}{7} & = & \frac{-4 \times 7}{5 \times 7} + \frac{ | -\frac{4}{5} + \frac{3}{7} & = & \frac{-4 \times 7}{5 \times 7} + \frac{3 \times 5}{7 \times 5} \\ | ||
& = & \frac{-28}{35} +\frac{15}{35} \\ | |||
& = & \frac{-13}{35} \\ | |||
& = &- \frac{13}{35} | |||
\end{array} | \end{array} | ||
</math> | </math> | ||
| Line 918: | Line 933: | ||
<math> | <math> | ||
\begin{array}{lcl} | \begin{array}{lcl} | ||
-\frac{4}{5} - \frac{3}{7} & = & \frac{-4 \times 7}{5 \times 7} - \frac{ | -\frac{4}{5} - \frac{3}{7} & = & \frac{-4 \times 7}{5 \times 7} - \frac{3 \times 5}{7 \times 5} \\ | ||
& = & \frac{-28}{35} -\frac{15}{35} \\ | |||
& = & \frac{-43}{35} \\ | |||
& = &- 1\frac{8}{35} | |||
\end{array} | \end{array} | ||
</math> | </math> | ||
Beberapa contoh penjumlahan dan pengurangan bilangan pecahan negatif dapat dilihat dalam video ini | Beberapa contoh penjumlahan dan pengurangan bilangan pecahan negatif dapat dilihat dalam video ini | ||
| Line 942: | Line 956: | ||
== | == Pecahan Biasa dan Pecahan Majemuk == | ||
=== | === Pecahan Biasa ke Pecahan Majemuk === | ||
| Line 997: | Line 1,011: | ||
=== | === Pecahan Majemuk ke Pecahan Biasa === | ||
Bagaimana mengubah pecahan majemuk menjadi pecahan biasa atau pecahan murni? | Bagaimana mengubah pecahan majemuk menjadi pecahan biasa atau pecahan murni? | ||
| Line 1,038: | Line 1,052: | ||
\begin{array}{lcl} | \begin{array}{lcl} | ||
4\frac{3}{5}& = & 4 + \frac{3}{5} \\ | 4\frac{3}{5}& = & 4 + \frac{3}{5} \\ | ||
& = & \frac{20}{5} + \frac{3}{5} \\ | |||
& = & \frac{23}{5} | & = & \frac{23}{5} | ||
\end{array} | \end{array} | ||
| Line 1,044: | Line 1,058: | ||
Video ini menunjukan contoh-contoh mengubah pecahan majemuk menjadi pecahan biasa. | |||
{{#ev:YouTube | |||
|id= 49bF9cjeOY8 | |||
|width=640 | |||
|height=400 | |||
}} | |||
*Aktivitas 11 | |||
Tujuan: siswa mengerjakan secara cepat soal-soal mengenai penjumlahan pecahan dengan beda penyebut | |||
Mengerjakan Latihan 9 - 10 dari buku Pecahan (buku 4) | |||
== Titik Kritis == | |||
== | |||
Titik Kritis untuk pecahan dicapai kalau siswa sudah mampu menguasai penjumlahan dan pengurangan seperti berikut ini | Titik Kritis untuk pecahan dicapai kalau siswa sudah mampu menguasai penjumlahan dan pengurangan seperti berikut ini | ||
| Line 1,268: | Line 1,249: | ||
== | == Penjumlahan dan Pengurangan Pecahan Majemuk == | ||
Pada bagian ini kita belajar bagaiman melakukan penjumlahan dan pengurangan pecahan majemuk. | Pada bagian ini kita belajar bagaiman melakukan penjumlahan dan pengurangan pecahan majemuk. | ||
| Line 1,280: | Line 1,261: | ||
Pada model ini | Pada model ini Pecahan Majemuk positif ditambah Pecahan Majemuk positif. | ||
Contoh : <math> 2 \frac{5}{7} + 3 \frac{3}{8} </math> | Contoh : <math> 2 \frac{5}{7} + 3 \frac{3}{8} </math> | ||
| Line 1,291: | Line 1,272: | ||
<math> | <math> | ||
\begin{array}{lcl} | \begin{array}{lcl} | ||
\frac{5}{7} + \frac{3}{8} & = & \frac{5 \times 8}{7 \times 8} + \frac{ | \frac{5}{7} + \frac{3}{8} & = & \frac{5 \times 8}{7 \times 8} + \frac{3 \times 7}{8 \times 7} \\ | ||
& = & \frac{40}{56} + \frac{21}{56} \\ | |||
& = & \frac{61}{56} \\ | |||
& = & \frac{61}{56} \\ | & = & 1 \frac{5}{56} | ||
& = & 1\frac {5}{56} | |||
\end{array} | \end{array} | ||
</math> | </math> | ||
| Line 1,319: | Line 1,299: | ||
Pada model ini | Pada model ini Pecahan Majemuk negatif ditambah Pecahan Majemuk negatif. | ||
Contoh : <math> -2 \frac{5}{7} - 3 \frac{3}{8} </math> | Contoh : <math> -2 \frac{5}{7} - 3 \frac{3}{8} </math> | ||
| Line 1,329: | Line 1,309: | ||
<math> | <math> | ||
\begin{array}{lcl} | \begin{array}{lcl} | ||
-\frac{5}{7} - \frac{3}{8} & = & \frac{-5 \times 8}{7 \times 8} - \frac{ | -\frac{5}{7} - \frac{3}{8} & = & \frac{-5 \times 8}{7 \times 8} - \frac{3 \times 7}{8 \times 7} \\ | ||
& = & \frac{ | & = & -\frac{40}{56} - \frac{21}{56} \\ | ||
& = & \frac{-61}{56} \\ | & = & \frac{-61}{56} \\ | ||
& = & -1\frac {5}{56} | & = & -1\frac {5}{56} | ||
| Line 1,356: | Line 1,335: | ||
=== model 3 : <math> 2\frac{2}{5} - 3\frac{3}{7} </math> === | === model 3 : <math> 2\frac{2}{5} - 3\frac{3}{7} </math> === | ||
Pada model ini | Pada model ini Pecahan Majemuk positif dikurangi Pecahan Majemuk positif. | ||
Contoh : <math> 2 \frac{5}{7} - 3 \frac{3}{8} </math> | Contoh : <math> 2 \frac{5}{7} - 3 \frac{3}{8} </math> | ||
| Line 1,368: | Line 1,347: | ||
\begin{array}{lcl} | \begin{array}{lcl} | ||
\frac{5}{7} - \frac{3}{8} & = & \frac{5 \times 8}{7 \times 8} - \frac{7 \times 3}{7 \times 8} \\ | \frac{5}{7} - \frac{3}{8} & = & \frac{5 \times 8}{7 \times 8} - \frac{7 \times 3}{7 \times 8} \\ | ||
& = & \frac{ | & = & \frac{40}{56} - \frac{21}{56} \\ | ||
& = & \frac{19}{56} | & = & \frac{19}{56} | ||
\end{array} | \end{array} | ||
| Line 1,392: | Line 1,370: | ||
=== model 4 : <math> -2\frac{2}{5} + 3\frac{3}{7} </math> === | === model 4 : <math> -2\frac{2}{5} + 3\frac{3}{7} </math> === | ||
Pada model ini | Pada model ini Pecahan Majemuk negatif ditambah Pecahan Majemuk positif. | ||
Contoh : <math> -2 \frac{5}{7} + 3 \frac{3}{8} </math> | Contoh : <math> -2 \frac{5}{7} + 3 \frac{3}{8} </math> | ||
| Line 1,403: | Line 1,381: | ||
\begin{array}{lcl} | \begin{array}{lcl} | ||
-\frac{5}{7} + \frac{3}{8} & = & \frac{-5 \times 8}{7 \times 8} + \frac{7 \times 3}{7 \times 8} \\ | -\frac{5}{7} + \frac{3}{8} & = & \frac{-5 \times 8}{7 \times 8} + \frac{7 \times 3}{7 \times 8} \\ | ||
& = & -\frac{40}{56} + \frac{21}{56} \\ | |||
& = & \frac{-19}{56} | & = & \frac{-19}{56} | ||
\end{array} | \end{array} | ||
| Line 1,435: | Line 1,412: | ||
== | == Perkalian Pecahan == | ||
Pembahasan perkalian pecahan akan kita bagi dalam 4 bagian | Pembahasan perkalian pecahan akan kita bagi dalam 4 bagian | ||
| Line 1,445: | Line 1,422: | ||
=== | === Bilangan Bulat x bilangan Pecahan === | ||
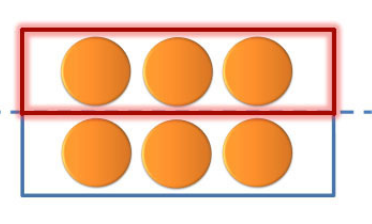
:Perkalian pecahan menggunakan dasar konsep perkalian yang sudah dipelajari sebelumnya. | :Perkalian bilangan pecahan menggunakan dasar konsep perkalian bilangan bulat yang sudah dipelajari sebelumnya. | ||
:Dalam perkalian kita tentu masih ingat bahwa 3 x 2 artinya 3 kotak isi 2, yaitu konkretnya ada 3 kotak yang masing-masing isinya 2. | :Dalam perkalian bilangan bulat kita tentu masih ingat bahwa 3 x 2 artinya 3 kotak isi 2, yaitu konkretnya ada 3 kotak yang masing-masing isinya 2 benda. | ||
[[Image:Screen Shot 2022-02-23 at 04.23.02.png|400px]] | [[Image:Screen Shot 2022-02-23 at 04.23.02.png|400px]] | ||
| Line 1,455: | Line 1,432: | ||
:Sekarang bagaimana dengan 2 x <small><math>\frac{1}{2}</math></small> ? | :Sekarang bagaimana dengan 2 x <small><math>\frac{1}{2}</math></small> ? | ||
: 2 x <small><math>\frac{1}{2}</math></small> artinya 2 kotak isi <small><math>\frac{1}{2}</math></small> | : 2 x <small><math>\frac{1}{2}</math></small> artinya 2 kotak isi <small><math>\frac{1}{2}</math></small> | ||
: Konkretnya ada 2 kotak yang masing-masing berisi <small><math>\frac{1}{2}</math></small> | : Konkretnya ada 2 kotak yang masing-masing berisi <small><math>\frac{1}{2}</math></small> benda. | ||
[[Image:Screen Shot 2022-02-23 at 04.23.35.png|300px]] | [[Image:Screen Shot 2022-02-23 at 04.23.35.png|300px]] | ||
| Line 1,465: | Line 1,442: | ||
Begitu pula | Begitu pula | ||
:3 x <small><math>\frac{1}{2}</math></small> = 3▢<small><math>\frac{1}{2}</math></small> = <small><math>\frac{1}{2}</math></small> + <small><math>\frac{1}{2}</math></small> + <small><math>\frac{ | :3 x <small><math>\frac{1}{2}</math></small> = 3▢<small><math>\frac{1}{2}</math></small> = <small><math>\frac{1}{2}</math></small> + <small><math>\frac{1}{2}</math></small> + <small><math>\frac{1}{2}</math></small> = <small><math>\frac{3}{2}</math></small> | ||
Kongkretnya digambarkan sebagai 3 kotak masing-masing berisi <small><math>\frac{3}{2}</math></small> | Kongkretnya digambarkan sebagai 3 kotak masing-masing berisi <small><math>\frac{3}{2}</math></small> | ||
| Line 1,496: | Line 1,473: | ||
=== | === Bilangan Pecahan x Bilangan Bulat === | ||
| Line 1,502: | Line 1,479: | ||
: <small><math>\frac{1}{2}</math></small> x 6 artinya <small><math>\frac{1}{2}</math></small> kotak isi 6. | : <small><math>\frac{1}{2}</math></small> x 6 artinya <small><math>\frac{1}{2}</math></small> kotak isi 6. | ||
:Jadi konkretnya ada 6 kue dalam suatu kotak lalu kita bagi kotak tersebut menjadi 2 bagian yang sama besar (sehingga banyaknya kue dalam tiap bagian sama). lalu kita hitung berapa isi | :Jadi konkretnya ada 6 kue dalam suatu kotak lalu kita bagi kotak tersebut menjadi 2 bagian yang sama besar (sehingga banyaknya kue dalam tiap bagian sama). lalu kita hitung berapa isi 1 bagiannya itu. | ||
:Hasilnya adalah 3 | :Hasilnya adalah 3 | ||
| Line 1,532: | Line 1,509: | ||
Perhatikan hasil-hasil yang kita peroleh | Perhatikan hasil-hasil yang kita peroleh | ||
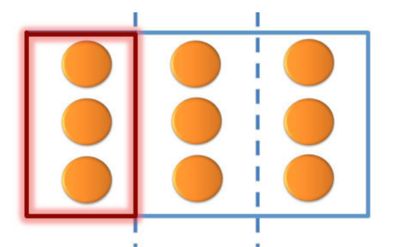
::<small><math>\frac{1}{2}</math></small> x 6 hasilnya sama dengan 6÷2 yaitu 3 | ::<small><math>\frac{1}{2}</math></small> x 6 hasilnya sama dengan membayangkan 6÷2 yaitu 3 | ||
::<small><math>\frac{1}{3}</math></small> x 6 hasilnya sama dengan 6÷3 yaitu 2 | ::<small><math>\frac{1}{3}</math></small> x 6 hasilnya sama dengan membayangkan 6÷3 yaitu 2 | ||
::<small><math>\frac{1}{3}</math></small> x 9 hasilnya sama dengan 9÷3 yaitu 3 | ::<small><math>\frac{1}{3}</math></small> x 9 hasilnya sama dengan membayangkan 9÷3 yaitu 3 | ||
Kesimpulan apa yang kita peroleh? | Kesimpulan apa yang kita peroleh? | ||
| Line 1,545: | Line 1,522: | ||
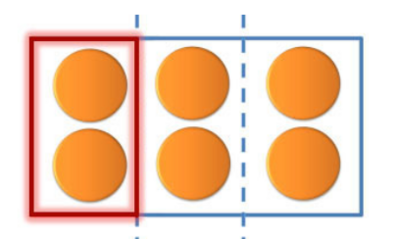
:Bagaimana dengan <small><math>\frac{2}{3}</math></small> x 9 = ? | :Bagaimana dengan <small><math>\frac{2}{3}</math></small> x 9 = ? | ||
: <small><math>\frac{2}{3}</math></small> artinya | : <small><math>\frac{2}{3}</math></small> x 9 artinya <small><math>\frac{2}{3}</math></small> kotak isi 9, jadi konkretnya ada 9 benda dalam suatu kotak lalu kita bagi kotak tersebut menjadi 3 bagian yang sama besar (sehingga banyaknya kue dalam tiap bagian sama). Lalu kita hitung berapa isi dua bagian kotak itu? | ||
: Hasilnya adalah 2 x 3 = 6 benda | |||
Hasilnya dapat digambarkan sebagai berikut. Hasilnya adalah 6 kue yang ada dalam daerah yang diarsir. | |||
[[Image:Screen Shot 2022-02-23 at 05.09.42.png|400px]] | [[Image:Screen Shot 2022-02-23 at 05.09.42.png|400px]] | ||
Berikut ini beberapa contoh perkalian pecahan dengan bilangan bulat | Berikut ini beberapa contoh perkalian pecahan dengan bilangan bulat | ||
:a) <small><math>\frac{3}{4}</math></small> x 12 = ? | :a) <small><math>\frac{3}{4}</math></small> x 12 = ? | ||
: <small><math>\frac{3}{4}</math></small> artinya | : <small><math>\frac{3}{4}</math></small> x 12 artinya <small><math>\frac{3}{4}</math></small> kotak isi 12, jadi konkretnya ada 12 benda dalam suatu kotak lalu kita bagi kotak tersebut menjadi 4 bagian yang sama besar (sehingga banyaknya kue dalam tiap bagian sama). Lalu kita hitung berapa isi tiga bagian kotak itu? | ||
: Hasilnya adalah 3 x 3 = 9 benda | |||
[[Image:Screen Shot 2022-02-23 at 05.10.06.png|400px]] | [[Image:Screen Shot 2022-02-23 at 05.10.06.png|400px]] | ||
| Line 1,565: | Line 1,540: | ||
:b) <small><math>\frac{5}{6}</math></small> x 30 = ? | :b) <small><math>\frac{5}{6}</math></small> x 30 = ? | ||
: <small><math>\frac{5}{6}</math></small> artinya | : <small><math>\frac{5}{6}</math></small> x 30 artinya <small><math>\frac{5}{6}</math></small> kotak isi 30, jadi konkretnya ada 30 benda dalam suatu kotak lalu kita bagi kotak tersebut menjadi 6 bagian yang sama besar (sehingga banyaknya kue dalam tiap bagian sama). Lalu kita hitung berapa isi lima bagian kotak itu? | ||
: | : Hasilnya adalah 5 x 5 = 25 benda | ||
<small><math>\frac{5}{6}</math></small> x 30 = 25 | |||
[[Image:Screen Shot 2022-02-23 at 05.10.32.png|400px]] | [[Image:Screen Shot 2022-02-23 at 05.10.32.png|400px]] | ||
| Line 1,573: | Line 1,550: | ||
:c) <small><math>\frac{5}{7}</math></small> x 49 = ? | :c) <small><math>\frac{5}{7}</math></small> x 49 = ? | ||
: <small><math>\frac{5}{7}</math></small> artinya | : <small><math>\frac{5}{7}</math></small> x 49 artinya <small><math>\frac{5}{7}</math></small> kotak isi 49, jadi konkretnya ada 49 benda dalam suatu kotak lalu kita bagi kotak tersebut menjadi 7 bagian yang sama besar (sehingga banyaknya kue dalam tiap bagian sama). Lalu kita hitung berapa isi lima bagian kotak itu? | ||
: | : Hasilnya adalah 7x 5 =35 benda | ||
<small><math>\frac{5}{7}</math></small> x 49 = 35 | |||
[[Image:Screen Shot 2022-02-23 at 05.10.38.png|400px]] | [[Image:Screen Shot 2022-02-23 at 05.10.38.png|400px]] | ||
| Line 1,581: | Line 1,559: | ||
:d) <small><math>\frac{7}{9}</math></small> x 18 = ? | :d) <small><math>\frac{7}{9}</math></small> x 18 = ? | ||
: <small><math>\frac{7}{9}</math></small> artinya | : <small><math>\frac{7}{9}</math></small> x 18 artinya <small><math>\frac{7}{9}</math></small> kotak isi 18, jadi konkretnya ada 18 benda dalam suatu kotak lalu kita bagi kotak tersebut menjadi 9 bagian yang sama besar (sehingga banyaknya kue dalam tiap bagian sama). Lalu kita hitung berapa isi tujuh bagian kotak itu? | ||
: Hasilnya adalah 2x7 = 14 benda | |||
[[Image:Screen Shot 2022-02-23 at 05.10.44.png|400px]] | [[Image:Screen Shot 2022-02-23 at 05.10.44.png|400px]] | ||
| Line 1,600: | Line 1,579: | ||
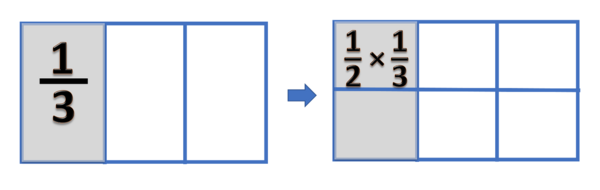
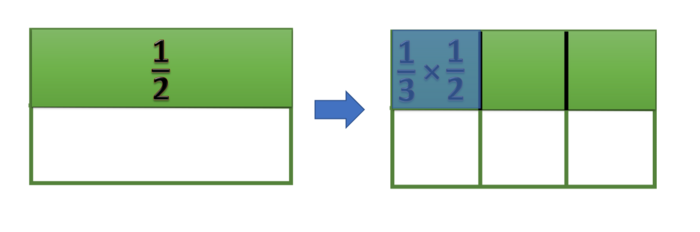
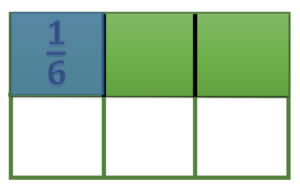
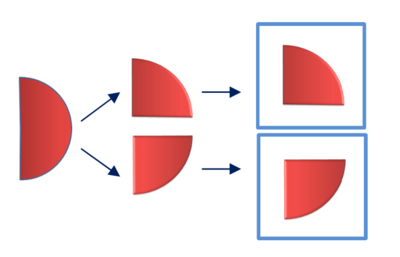
=== | === Pecahan x Pecahan === | ||
Pada bab ini kita akan belajar tentang perkalian pecahan biasa dengan pecahan biasa, seperti <small><math>\frac{2}{5} \times \frac{3}{7}</math></small> | Pada bab ini kita akan belajar tentang perkalian pecahan biasa dengan pecahan biasa, seperti <small><math>\frac{2}{5} \times \frac{3}{7}</math></small> | ||
| Line 1,796: | Line 1,775: | ||
=== | === Pecahan Majemuk x Pecahan Majemuk === | ||
| Line 1,852: | Line 1,831: | ||
=== | === Perkalian 3 Pecahan === | ||
Pada perkalian 3 pecahan kita bisa lakukan dengan sistem coret. | Pada perkalian 3 pecahan kita bisa lakukan dengan sistem coret. | ||
| Line 1,872: | Line 1,851: | ||
Mengerjakan Latihan 28 dari buku Pecahan (buku 4) | Mengerjakan Latihan 28 dari buku Pecahan (buku 4) | ||
== | == Pembagian Pecahan == | ||
| Line 1,882: | Line 1,861: | ||
* Pembagian pecahan majemuk | * Pembagian pecahan majemuk | ||
=== Bilangan Pecahan ÷ Bilangan Bulat === | |||
:Pembagian pecahan menggunakan dasar konsep pembagian yang sudah dipelajari sebelumnya. | |||
:Dalam pembagian kita tentu masih ingat bahwa 6 ÷ 2 artinya saya punya 6 benda hendak dimasukan dalam 2 kotak, berapa yang diterima tiap kotak. | |||
:Kita sudah tahu bahwa jawabnya adalah 3 benda. | |||
: | : Bagaimana dengan pembagian bilangan pecahan dengan bilangan bulat seperti <small><math>\frac{1}{2}</math></small> ÷ 2 ? | ||
: | : <small><math>\frac{1}{2}</math></small> ÷ 2 artinya <small><math>\frac{1}{2}</math></small> kue hendak dimasukan dalam 2 kotak. Berapa isi masing-masing kotak agar pembagian ini adil dan merata. | ||
[[Image:Screen Shot 2022-02-24 at 20.51.36.png|400px]] | |||
Yang kita perlu lakukan adalah membagi dua kue <small><math>\frac{1}{2}</math></small> itu. Kemudian memasukan tiap bagian ke dalam kotak. Kita lihat tiap kotak akan menerima masing-masing <small><math>\frac{1}{4}</math></small> kue. | |||
Dengan demikian <small><math>\frac{1}{2}</math></small> ÷ 2 = <small><math>\frac{1}{4}</math></small> | |||
:Sekarang bagaimana dengan <small><math>\frac{1}{3}</math></small> : 2 = ? | |||
Kita bisa gunakan papan pecahan. | |||
Ini pecahan <small><math>\frac{1}{3}</math></small> | |||
[[Image:Screen Shot 2022-02-24 at | [[Image:Screen Shot 2022-02-24 at 21.08.06.png|400px]] | ||
Cari di papan pecahan, pecahan yang nilainya <small><math>\frac{1}{3}</math></small> tapi terbagi 2. | |||
Jawabnya adalah pada gambar ini | |||
: | [[Image:Screen Shot 2022-02-24 at 21.08.17.png|400px]] | ||
Disini terlihat bahwa <small><math>\frac{1}{3} : 2 = \frac{1}{6} </math></small> | |||
: | :Bagaimana dengan <small><math>\frac{1}{2}</math></small> ÷ 5 = ? | ||
Kita bisa gunakan papan pecahan. | |||
Ini pecahan <small><math>\frac{1}{2}</math></small> | |||
: | [[Image:Screen Shot 2022-02-24 at 21.13.37.png|400px]] | ||
Cari di papan pecahan, pecahan yang nilainya <small><math>\frac{1}{2}</math></small> tapi terbagi 5. | |||
Jawabnya adalah pada gambar ini | |||
[[Image:Screen Shot 2022-02-24 at 21.14.05.png|400px]] | |||
Disini terlihat bahwa <small><math>\frac{1}{2} : 5 = \frac{1}{10} </math></small> | |||
: | |||
Perhatikan hasil-hasil yang kita peroleh dibawah ini | |||
::<small><math>\frac{1}{2}</math></small> ÷ 6, kita membayangkan 1/2 kue dipotong-potong jadi 6 bagian yang sama hasilnya yaitu <small><math>\frac{1}{12}</math></small> | |||
::<small><math>\frac{1}{3}</math></small> ÷ 4, kita membayangkan 1/3 kue dipotong-potong jadi 4 bagian yang sama hasilnya yaitu <small><math>\frac{1}{12}</math></small> | |||
::<small><math>\frac{1}{5}</math></small> ÷ 7, kita membayangkan 1/5 kue dipotong-potong menjadi 7 bagian yang sama hasilnya yaitu <small><math>\frac{1}{35}</math></small> | |||
Video berikut menunjukan beberapa contoh perkalian bilangan pecahan dengan bilangan bulat. | |||
{{#ev:YouTube | {{#ev:YouTube | ||
|id= | |id= DBSXhkjXA7o | ||
|width=640 | |width=640 | ||
|height=400 | |height=400 | ||
}} | }} | ||
=== Bilangan Bulat ÷ Bilangan Pecahan === | |||
: Kalimat perkalian 2 x 3 = 6, artinya jika ada 2 kotak masing-masing kotak isi 3 benda maka jumlah seluruh benda dalam kotak-kotak itu adalah 6 benda. | |||
: Dari perkalian 2 x 3 = 6, maka arti pembagian 6:2 = 3 adalah kita punya 6 benda hendak dibagikan dalam 2 kotak, maka isi tiap kotak adalah 3 benda. | |||
: Dari perkalian 2 x 3 = 6, maka arti pembagian 6:3 = 2 adalah kita punya 6 benda hendak dimasukan dalam kotak, setiap kotak hanya bisa menampung 3 benda, maka jumlah kotak yang bisa menerima 6 benda ini ada 2 kotak. | |||
Disini kita lihat ada 2 arti pembagian. Pembagian pertama yang sering kita pakai adalah menanyakan isi kotak. Sedangkan pembagian kedua adalah menanyakan banyak kotak. | |||
Untuk perkalian bilangan bulat x bilangan pecahan, kita akan gunakan arti pembagian kedua. | |||
: | Contoh: | ||
1÷ <small><math>\frac{1}{2}</math></small>= ? | |||
Untuk melihat konkretnya ada baiknya kita ambil wadah air 1 liter dan wadah air 1/2 liter. | |||
Air dituang dari wadah 1 liter ke wadah 1/2 liter... kita lihat bahwa kita membutuhkan 2 wadah yang 1/2 liter. | |||
Jadi 1÷ <small><math>\frac{1}{2}</math></small>= 2 | |||
:Bagaimana dengan pembagian 1 ÷ <small><math>\frac{1}{2}</math></small> ? | |||
:Saya punya kue hendak dimasukan dalam kotak dengan kapasitas atau ukuran <small><math>\frac{1}{2}</math></small>, berapa banyak potong kue dapat dimasukan dalam kotak tersebut? | |||
[[Image:Screen Shot 2022-02-24 at 11.44.58.png|300px]] | |||
Gambar dibawah ini menggambarkan situasi ketika 1 potong kue sudah masuk kotak pertama. | |||
[[Image:Screen Shot 2022-02-24 at 11.45.20.png|300px]] | |||
Ini gambar situasi ketika 2 potong kue sudah masuk kotak kedua. | |||
[[Image:Screen Shot 2022-02-24 at 11.45.59.png|300px]] | |||
Jadi jumlah kotak yang dibutuhkan adalah 2 kotak. | |||
Sekarang kita akan hitung 1 ÷ <small><math>\frac{1}{4}</math></small> | |||
[[Image:Screen Shot 2022-02-24 at | [[Image:Screen Shot 2022-02-24 at 12.16.41.png|300px]] | ||
:Pada gambar diatas kita punya 1 kue, hendak kita masukan dalam beberapa kotak dengan kapasitas atau ukuran <small><math>\frac{1}{4}</math></small>. | |||
:Kue kita bagi menjadi potongan <small><math>\frac{1}{4}</math></small> agar bisa masuk kotak. | |||
:Kita lihat bahwa banyak kotak adalah 4 buah. | |||
Jadi | |||
:1 ÷ <small><math>\frac{1}{4}</math></small> = 4 | |||
Bisa juga kita gunakan wadah 1 liter dan wadah 1/4 liter. Air dalam wadah 1 liter kita tuangkan dalam wadah 1/4 liter dan kita bisa lihat bahwa untuk ini dibutuhkan 4 wadah. Jadi | |||
1 ÷ <small><math>\frac{1}{4}</math></small> = 4 | |||
Dengan cara yang sama kita bisa dapatkan bahwa | |||
:1 ÷ <small><math>\frac{1}{3}</math></small> = 3 | |||
:1 ÷ <small><math>\frac{1}{6}</math></small> = 6 | |||
:1 ÷ <small><math>\frac{1}{10}</math></small> = 10 | |||
Pola apa yang Anda lihat? | |||
:Bagaimana kalau 2 ÷ <small><math>\frac{1}{2}</math></small> = ? | |||
: Karena | |||
:: 1 ÷ <small><math>\frac{1}{2}</math></small> = 2 | |||
:maka | |||
:: 2 ÷ <small><math>\frac{1}{2}</math></small> = 2 x 2 = 4 | |||
[[Image:Screen Shot 2022-02-24 at 12.24.19.png|300px]] | |||
Dengan cara yang sama kita bisa peroleh | |||
: | :2 ÷ <small><math>\frac{1}{3}</math></small> = 2 x 3 = 6 | ||
: | :2 ÷ <small><math>\frac{1}{4}</math></small> = 2 x 4 = 8 | ||
: | :2 ÷ <small><math>\frac{1}{6}</math></small> = 2 x 6 = 12 | ||
:2 ÷ <small><math>\frac{1}{10}</math></small> = 2 x 10 = 20 | |||
Dan dengan pola yang sama kita bisa peroleh | |||
:5 ÷ <small><math>\frac{1}{3}</math></small> = 5 x 3 = 15 | |||
:9 ÷ <small><math>\frac{1}{4}</math></small> = 9 x 4 = 36 | |||
:12 ÷ <small><math>\frac{1}{6}</math></small> = 12 x 6 = 72 | |||
:25 ÷ <small><math>\frac{1}{10}</math></small> = 25 x 10 = 250 | |||
Jadi resep untuk menghitung perbagian bilangan bulat dengan bilangan pecahan seperti 25 ÷ <small><math>\frac{1}{10}</math></small> adalah dengan membayangkan 1 kali÷ <small><math>\frac{1}{10}</math></small>. Kemudian hasilnya ini dikalikan 25. Hasilnya adalah 250. | |||
Video berikut menunjukan | Video berikut menunjukan berbagai contoh pembagian bilangan bulat dengan pecahan. | ||
{{#ev:YouTube | {{#ev:YouTube | ||
|id= | |id= RbJ0IYVfnss | ||
|width=640 | |width=640 | ||
|height=400 | |height=400 | ||
}} | }} | ||
=== | |||
=== Pecahan ÷ Pecahan === | |||
Pada bagian ini kita akan belajar tentang pembagian pecahan biasa dengan pecahan biasa, seperti <small><math>\frac{2}{5} \div \frac{3}{7}</math></small> | Pada bagian ini kita akan belajar tentang pembagian pecahan biasa dengan pecahan biasa, seperti <small><math>\frac{2}{5} \div \frac{3}{7}</math></small> | ||
| Line 2,062: | Line 2,038: | ||
Misalkan kita akan menghitung <small><math>\frac{1}{2}</math></small> ÷ <small><math>\frac{1}{4}</math></small> | Misalkan kita akan menghitung <small><math>\frac{1}{2}</math></small> ÷ <small><math>\frac{1}{4}</math></small> | ||
<math>\frac{1}{2} \div \frac{1}{4}</math> artinya ada kue berukuran <small><math>\frac{1}{2}</math></small> hendak dimasukan dalam kotak berukuran <small><math>\frac{1}{4}</math></small>, ada berapa | <math>\frac{1}{2} \div \frac{1}{4}</math> artinya ada kue berukuran <small><math>\frac{1}{2}</math></small> hendak dimasukan dalam kotak berukuran <small><math>\frac{1}{4}</math></small>, ada berapa banyak kotak dibutuhkan? | ||
[[Image:Screen Shot 2022-02-25 at 05.07.18.png|300px]] | [[Image:Screen Shot 2022-02-25 at 05.07.18.png|300px]] | ||
| Line 2,075: | Line 2,051: | ||
Kue yang sudah dipotong ini dimasukan satu persatu ke dalam kotak <small><math>\frac{1}{4}</math></small>. | Kue yang sudah dipotong ini dimasukan satu persatu ke dalam kotak <small><math>\frac{1}{4}</math></small>. | ||
Banyak | Banyak kotak yang dibutuhkan adalah 2 buah. | ||
:: Dengan demikian <small><math>\frac{1}{2} \div \frac{1}{4}</math></small> = 2 | :: Dengan demikian <small><math>\frac{1}{2} \div \frac{1}{4}</math></small> = 2 | ||
Kita bisa juga lakukan ini dengan wadah 1/2 liter air dan wadah 1/4 liter air. Kita masukan air dari wadah 1/2 liter ke wadah 1/4 liter. Kita lihat bahwa kita butuh 2 wadah. Jadi | |||
<small><math>\frac{1}{2} \div \frac{1}{4}</math></small> = 2 | |||
| Line 2,087: | Line 2,066: | ||
[[Image:Screen Shot 2022-02-25 at 03.30.29.png|300px]] | [[Image:Screen Shot 2022-02-25 at 03.30.29.png|300px]] | ||
<math>\frac{1}{2} \div \frac{1}{4}</math> artinya ada batang <small><math>\frac{1}{2}</math></small> hendak dimasukan dalam kotak <small><math>\frac{1}{4}</math></small>, ada berapa buah | <math>\frac{1}{2} \div \frac{1}{4}</math> artinya ada batang <small><math>\frac{1}{2}</math></small> hendak dimasukan dalam kotak <small><math>\frac{1}{4}</math></small>, ada berapa buah kotak dibutuhkan. | ||
Pecahan <small><math>\frac{1}{2}</math></small> terlalu besar untuk masuk kotak <small><math>\frac{1}{4}</math></small>. Karena itu maka pecahan <small><math>\frac{1}{2}</math></small> itu harus dipotong menjadi beberapa potongan pecahan <small><math>\frac{1}{4}</math></small>. | Pecahan <small><math>\frac{1}{2}</math></small> terlalu besar untuk masuk kotak <small><math>\frac{1}{4}</math></small>. Karena itu maka pecahan <small><math>\frac{1}{2}</math></small> itu harus dipotong menjadi beberapa potongan pecahan <small><math>\frac{1}{4}</math></small>. | ||
| Line 2,097: | Line 2,076: | ||
Potongan pecahan <small><math>\frac{1}{4}</math></small> ini \kemudian dimasukan satu persatu ke dalam kotak <small><math>\frac{1}{4}</math></small>. | Potongan pecahan <small><math>\frac{1}{4}</math></small> ini \kemudian dimasukan satu persatu ke dalam kotak <small><math>\frac{1}{4}</math></small>. | ||
Banyak | Banyak kotak yang dibutuhkan adalah 2 buah. | ||
:: Dengan demikian <small><math>\frac{1}{2} \div \frac{1}{4}</math></small> = 2 | :: Dengan demikian <small><math>\frac{1}{2} \div \frac{1}{4}</math></small> = 2 | ||
| Line 2,107: | Line 2,086: | ||
* Arti <small><math>\frac{1}{2} \div \frac{1}{8}</math></small> adalah kita mempunyai pecahan <small><math>\frac{1}{2} </math></small> | * Arti <small><math>\frac{1}{2} \div \frac{1}{8}</math></small> adalah kita mempunyai pecahan <small><math>\frac{1}{2} </math></small> | ||
hendak dimasukan dalam kotak berukuran <small><math>\frac{1}{8} </math></small>, tentunya pecahan itu harus dipotong-potong. Ada berapa | hendak dimasukan dalam kotak berukuran <small><math>\frac{1}{8} </math></small>, tentunya pecahan itu harus dipotong-potong. Ada berapa kotak <small><math>\frac{1}{8} </math></small> dibutuhkan? | ||
* Cari di papan pecahan, pecahan <small><math>\frac{1}{2} </math></small> | * Cari di papan pecahan, pecahan <small><math>\frac{1}{2} </math></small> | ||
| Line 2,114: | Line 2,093: | ||
* Tempatkan pecahan <small><math>\frac{1}{2} </math></small> ini ke dalam deretan pecahan <small><math>\frac{1}{8}</math></small>. Kita lihat | * Tempatkan pecahan <small><math>\frac{1}{2} </math></small> ini ke dalam deretan pecahan <small><math>\frac{1}{8}</math></small>. Kita lihat | ||
ada 4 pecahan <small><math>\frac{1}{8}</math></small> yang nilainya <small><math>\frac{1}{2} </math></small>. | ada 4 pecahan <small><math>\frac{1}{8}</math></small> yang nilainya <small><math>\frac{1}{2} </math></small>. Dengan kata lain ada 4 kotak <small><math>\frac{1}{8}</math></small> dibutuhkan untuk menampung <small><math>\frac{1}{2} </math></small>. | ||
[[Image:Screen Shot 2022-02-25 at 03.46.23.png|300px]] | [[Image:Screen Shot 2022-02-25 at 03.46.23.png|300px]] | ||
Latest revision as of 22:15, 28 December 2023
Gasing Berhitung: Pecahan
Untuk belajar pecahan kita perlu melewati beberapa langkah sebagai berikut:
- Arti pecahan
- Pecahan senilai dan penyederhanaan pecahan
- Penjumlahan dan pengurangan pecahan dengan penyebut yang sama atau berbeda
- Konsep ‘SATU’ dan pecahan adalah bagi
- Pecahancampuran
- Titik kritis GASING
Untuk titik kritis Gasing dalam operasi penjumlahan dan pengurangan adalah siswa mampu mengerjakan 4 jenis operasi ini secara cepat.
Selanjutnya setelah menguasai operasi penjumlahan dan pengurangan, maka operasi perkalian dan pembagian pecahan dapat dilakukan dengan mudah.
Arti Pecahan
Pecahan adalah suatu simbol yang terdiri dari 2 angka yang dipisahkan oleh satu garis.
Pecahan ini adalah simbol yang tidak punya arti apa-apa kalau tidak diberi konteks.
Sama seperti bilangan bulat, bilangan bulat itu hanyalah simbol-simbol berupa angka 0,1,2, 3...9 yang tidak ada makna apa-apa kalau tidak diberi konteks.
Maksudnya apa?
Misalnya
5 Jeruk.
Konteksnya adalah jeruk.
Ketika 5 dihubungkan dengan jeruk, maka 5 itu menunjukan jumlah jeruk sebanyak lima buah.
Bagaimana memberi konteks pecahan?
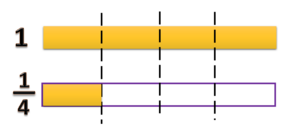
Pada gambar di atas, angka 1 kita beri konteks batang (berat atau panjangnya).
Gambar pertama ada 1 batang. Kita sebut nilai batang ini adalah 1 batang.
1 Batang pada gambar pertama kita potong menjadi 2 bagian yang sama nilainya.
Satu potongan kita sebut nilainya batang.
- diartikan sebagai nilai satu bagian dari satu kelompok yang terdiri dari dua bagian yang sama nilainya.
Bagaimana jika 1 batang pada gambar pertama itu kita potong menjadi 4 bagian yang sama nilainya.
Potongan ini kita sebut nilainya batang.
- diartikan sebagai nilai satu bagian dari satu kelompok yang terdiri dari empat bagian yang sama nilainya.
Contoh lain:
- Ada 1 jeruk dipotong menjadi 2 bagian yang sama besar.
- 1 bagian jeruk nilainya adalah jeruk.
- Karena ini menunjukan satu bagian dari satu kelompok yang terdiri dari dua bagian jeruk yang sama nilainya.
Sekarang perhatikan gambar berikut ini:
Apakah potongan kuning atau potongan merah ini bernilai Jawabnya bisa ya bisa tidak tergantung konteksnya atau nilainya.
Jika konteksnya adalah warna benda, maka potongan kuning ini bernilai karena ini adalah satu warna dari satu kelompok yang terdiri dari dua warna (putih dan kuning) yang sama nilainya. Dalam hal ini nilainya adalah warna benda.
Hal yang sama berlaku untuk potongan merah.
Tetapi kalau konteksnya adalah luas benda, maka potongan kuning maupun potongan merah tidak bernilai
- Batang kuning dibagi menjadi 3 bagian sama besar
- Tiap bagian bernilai
- menunjukan nilai 1 bagian dari satu kelompok yang terdiri dari 3 bagian yang sama nilainya.
- Batang ungu dibagi menjadi 4 bagian sama besar
- Tiap bagian bernilai
- menunjukan nilai 1 bagian dari satu kelompok yang terdiri dari 4 bagian yang sama nilainya.
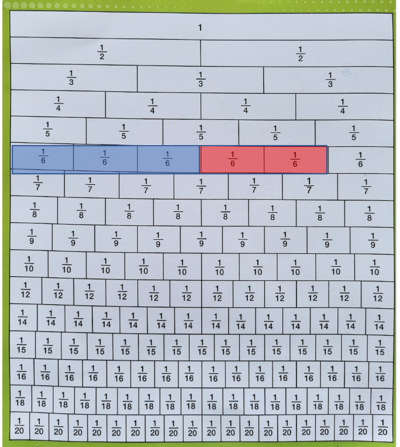
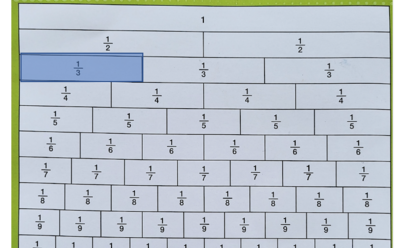
- 1 Lingkaran dibagi menjadi 8 bagian sama besar
- Bagian yang berwarna kuning bernilai
- menunjukan nilai 3 bagian dari satu kelompok yang terdiri dari 8 bagian yang sama besar.
- dibaca “1 garis 2” atau “1 per 2”.
- Angka yang diatas dinamakan pembilang
- Angka yang dibawah dinamakan penyebut
Lihat video berikut ini mengenai konsep pecahan.
{{#ev:YouTube |id= C4gB6iA70l4 |width=640 |height=400 }}
- Aktivitas 1
Tujuan: siswa mengerjakan secara cepat soal-soal mengenai konsep pecahan
Mengerjakan Latihan 1a dari buku Pecahan (buku 4)
- Aktivitas 2
Peserta membuat group 10 orang. Kemudian sebagian (misalnya 3 orang) berdiri dan sisanya duduk. Kita katakan orang yang berdiri nilainya adalah 3/10. Karena 3 orang dari kelompok yang terdiri dari 10 orang manusia yang nilainya sama yaitu sama-sama manusia.
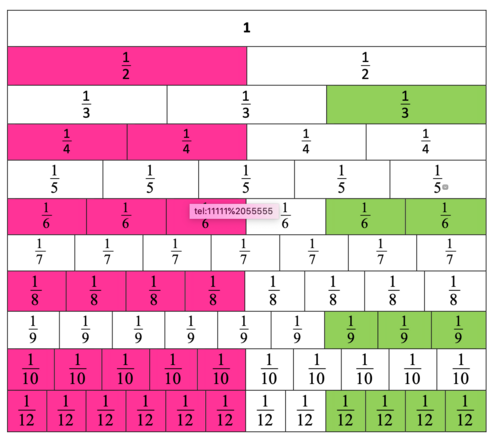
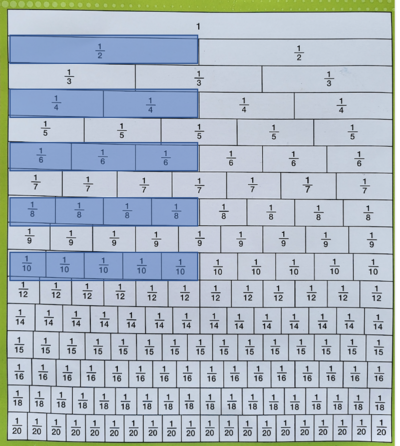
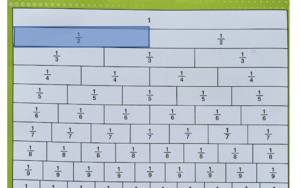
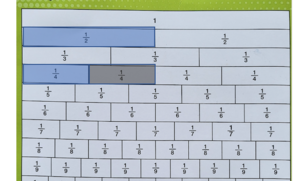
Pecahan Senilai
- Batang kuning atas bernilai
- Batang kuning bawah bernilai
- Kedua batang tersebut sama besar (sama nilainya) sehingga kita katakan keduanya senilai.
- senilai
- =
- Perhatikan: dan nilainya sama walaupun artinya berbeda
- artinya nilai 1 bagian dari kelompok yang terdiri dari 2 bagian yang sama nilainya
- artinya nilai 2 bagian dari kelompok yang terdiri dari 4 bagian yang sama nilainya
- Pada batang merah jambu
- = = = = =
- Pecahan ini semua bernilai sama
- Pada batang hijau
- = = =
- Pecahan ini semua bernilai sama
- bagaimana mendapatkan pecahan senilai?
- Dengan mengalikan pembilang dan penyebut dengan bilangan yang sama.
- bagaimana mendapatkan pecahan senilai?
Perhatikan beberapa contoh pecahan senilai dalam video dibawah ini.
{{#ev:YouTube
|id= PoTTD3yRsEg
|width=640
|height=400
}}
- Aktivitas 2
Tujuan: siswa mengerjakan secara cepat soal-soal mengenai pecahan senilai
Mengerjakan Latihan 2 dari buku Pecahan (buku 4)
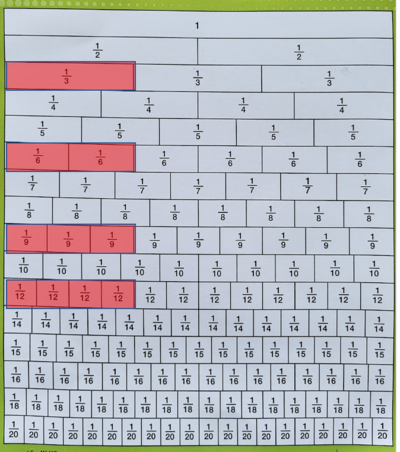
Menyederhanakan Pecahan
- Pecahan :: dapat disederhanakan menjadi
- Tapi bisa juga disederhanakan menjadi
Atau
Dari pecahan-pecahan senilai itu adalah yang nilai pembilang dan penyebutnya terkecil yaitu .
Pecahan dengan pembilang dan penyebutnya terkecil ini dinamakan pecahan sederhana.
Proses membuat suatu pecahan menjadi pecahan sederhana dinamakan proses penyederhanaan pecahan.
- Misal
- dapat disederhanakan menjadi
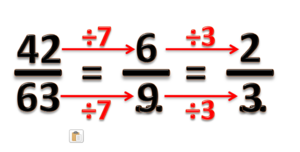
Cara menyederhanakan pecahan adalah membagi pembilang dan penyebut dengan suatu bilangan yang sama.
Untuk menyederhanakan :: menjadi kita dapat membagi pembilang dan penyebutnya dengan 3.
Untuk menyederhanakan menjadi kita dapat membagi pembilang dan penyebutnya dengan 6.
Untuk bilangan yang agak besar, kita dapat membagi pembilang dan penyebutnya berulang-ulang sampai kita dapat pecahan yang paling sederhana.
Beberapa contoh menyederhanakan pecahan bisa dilihat dalam video ini
{{#ev:YouTube
|id= PS1leZn06us
|width=640
|height=400
}}
- Aktivitas 3
Tujuan: siswa mengerjakan secara cepat soal-soal mengenai pecahan senilai
Mengerjakan Latihan 3 dari buku Pecahan (buku 4)
Operasi Penjumlahan dan Pengurangan Pecahan dengan Penyebut sama
Penjumlahan
Disini kita membatasi pembahasan pada nilai pembilang tidak melebihi nilai penyebut.
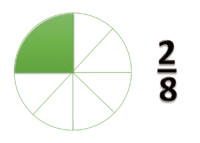
Gambar ini adalah pecahan
- menunjukan nilai 2 bagian dari suatu kelompok yang terdiri dari 8 bagian yang sama nilainya
- Kemudian kita tambahkan Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{8}}
- Kemudian kita tambahkan Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{8}}
- Hasilnya dengan mudah terlihat Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{3}{8}}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{3}{8}} menunjukan 3 bagian dari suatu kelompok yang terdiri dari 8 bagian yang sama nilainya.
Contoh lain:
Apa yang kita bisa simpulkan?
Dalam menjumlahkan pecahan dengan penyebut sama, kita hanya menambahkan pembilangnya saja sedangkan penyebut (atau kelompoknya) tetap sama.
Lihat video beberapa contoh penjumlahan pecahan dengan penyebut sama
{{#ev:YouTube |id= rJm6Rb-47eI |width=640 |height=400 }}
- Aktivitas 4
Tujuan: siswa mengerjakan secara cepat soal-soal mengenai pecahan senilai
Mengerjakan Latihan 4 dari buku Pecahan (buku 4)
Pengurangan
3 kotak biru dalam gambar ini menunjukan pecahan Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{3}{5} }
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{3}{5} } menunjukan nilai 3 bagian dari suatu kelompok yang terdiri dari 5 bagian yang sama nilainya.
Kemudian kita ambil dua kotak biru
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{3}{5} } - Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{5} }
Hasilnya terlihat sama dengan Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{5} }
- menunjukan nilai 1 bagian dari suatu kelompok yang terdiri dari 5 bagian yang sama nilainya.
Contoh lain:
Apa yang kita bisa simpulkan?
Dalam melakukan pengurangan pecahan dengan penyebut sama, kita hanya mengurangkan pembilangnya saja sedangkan penyebut (atau kelompoknya) tetap sama.
Lihat video untuk beberapa contoh pengurangan dengan penyebut sama.
{{#ev:YouTube
|id= k-N2vsimlQY
|width=640
|height=400
}}
- Aktivitas 5
Tujuan: siswa mengerjakan secara cepat soal-soal mengenai pengurangan dengan penyebut sama
Mengerjakan Latihan 14 dari buku Pecahan (buku 4)
Konsep SATU
Ini 1 jeruk, kita potong menjadi 2 bagian yang sama besar.
Satu bagian jeruk ini nilainya adalah Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2} } jeruk.
Karena itu maka
- (jeruk) + Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2} } (jeruk) = 1 (jeruk)
Atau kita hilangkan konteksnya, kita peroleh
- + Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2} } = 1
Namun kita tahu bahwa
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2} } + Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{2} }
Sehingga kita bisa simpulkan bahwa
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{2} } = 1
Contoh lain
Kita punya 1 batang kuning, kemudian batang itu kita potong menjadi 4 bagian yang sama nilainya.
- Berapa seperempat batang kuning ditambah seperempat batang kuning ditambah seperempat batang kuning ditambah seperempat batang kuning ?
- Jawabnya 1 batang kuning
- (batang kuning) + Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{4} } (batang kuning) + Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{4} } (batang kuning) + Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{4} } (batang kuning)= 1 (batang kuning)
Namun kita tahu bahwa
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{4} } + Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{4}} +Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{4} } + Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{4}} =
Sehingga boleh dikatakan bahwa
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{4}{4} } = 1
karena Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{2} }
= 1 dan Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{4}{4} }
= 1
maka kita boleh tuliskan,
- = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{4}{4} } = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{10}{10} } = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{178}{178} } = 1
Jadi bisa disimpulkan bahwa dalam pecahan arti bilangan 1 adalah sebagai berikut
- 1 adalah nilai 2 bagian dari satu kelompok yang terdiri dari 2 bagian yang sama nilainya.
- 1 adalah nilai 3 bagian dari satu kelompok yang terdiri dari 3 bagian yang sama nilainya.
- 1 adalah nilai 5 bagian dari satu kelompok yang terdiri dari 5 bagian yang sama nilainya.
Video berikut ini menjelaskan konsep "satu'
{{#ev:YouTube |id= U8rmQGhGgew |width=640 |height=400 }}
- Aktivitas 6
Tujuan: siswa mengerjakan secara cepat soal-soal mengenai konsep "satu"
Mengerjakan Latihan 5 dari buku Pecahan (buku 4)
Pecahan adalah Bagi
- Apakah pecahan itu adalah bagi?
- Apakah = 1 ÷ 2 ?
Untuk menjawab ini, mari kita lihat gambar ini
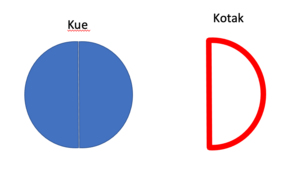
- Disini kita punya 1 kue berwarna hijau. Kue ini hendak dimasukan dalam 2 kotak secara adil, berapa isi masing-masing kotak?
- Untuk itu kita menuliskannya dalam bentuk 1 ÷ 2 = ?
- Jawabnya: isi masing-masing kotak adalah separuh kue
Sekarang kita perhatikan gambar separuh kue.
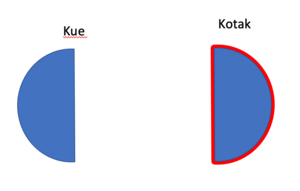
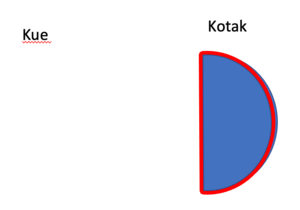
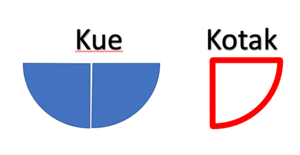
Menurut definisi pecahan,
- separuh atau setengah kue menunjukan nilai 1 bagian dari satu kue yang terdiri dari dua bagian yang sama nilainya.
- Ini ditulis Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2} } kue
Jadi kita bisa katakan bahwa
- Separuh kue adalah hasil pembagian dari 1 kue dibagi 2
- Separuh kue sama dengan Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2} } kue
Dengan demikian kita bisa katakan bahwa
:: 1 kue ÷ 2 nilainya sama dengan Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2} }
kue
ditulis
- 1 ÷ 2 = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2} }
Ini juga berlaku untuk pecahan-pecahan lain seperti:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{5} } nilainya sama dengan 1 dibagi 5
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{7} } nilainya sama dengan 1 dibagi 7
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{12} } nilainya sama dengan 1 dibagi 12
Sekarang kalau pembilangnya bukan 1, apakah "pecahan itu nilainya sama dengan pembagian" masih berlaku?
- Apakah Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{4}{2} } nilainya sama dengan 4 dibagi 2 ?
Untuk hal ini kita lihat pelajaran sebelumnya tentang 1.
- pada pelajaran sebelumnya 1 boleh didefinisikan sebagai nilai 2 bagian dari suatu kelompok yang terdiri dari 2 bagian yang sama besar.
Atau
- 1 = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{2} }
Dengan hasil itu kita bisa menulis,
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{4}{2}} = + Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{2} }
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{4}{2}} = 1 + 1 = 2
- Ternyata Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{4}{2}} = 2!
- pembagian 4 ÷ 2 hasilnya adalah 2 juga
Dengan demikian maka bisa dikatakan
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{4}{2}} nilainya sama dengan 4 dibagi 2 = 2
Jadi pecahan itu mempunyai kaitan yang erat dengan pembagian. Keduanya mempunyai nilai yang sama walaupun secara konsep berbeda.
Untuk jelasnya lihat video berikut ini
{{#ev:YouTube
|id= raii20Dvoxg
|width=640
|height=400
}}
- Aktivitas 7
Tujuan: siswa mengerjakan secara cepat soal-soal mengenai konsep pecahan dan bagi
Mengerjakan Latihan 7 dari buku Pecahan (buku 4)
Pecahan Majemuk
Berapa Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{3}} + Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{3}} ?
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{3}} + = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{4}{3}}
Kita bisa sederhanakan pecahan Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{3}} dengan menggunakan konsep satu atau konsep pecahan dan bagi.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{4}{3}} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{3}{3}} + Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{3}}
- Karena Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{3}{3}} = 1, maka
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{4}{3}} = 1 + Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{3}} = 1Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{3}}
Dimana kita definisikan bilangan bulat + pecahan sebagai bilangan bulat pecahan
- bentuk bilangan bulat pecahan seperti 1Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{3}} dinamakan pecahan campuran atau pecahan majemuk.
Perhatikan beberapa contoh berikut:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{5}{3}} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{3}{3}} + Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{3}} = 1Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{3}}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{7}{5}} = + Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{5}} = 1Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{5}}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{12}{7}} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{7}{7}} + Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{5}{7}} = 1Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{5}{12}}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{25}{23}} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{23}{23}} + Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{23}} = 1Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{23}}
- = + Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} = 3
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{11}{3}} = + Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{3}} = 3Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{3}}
Perhatikan contoh dalam video berikut
{{#ev:YouTube
|id= RFgSVEUixCc
|width=640
|height=400
}}
- Aktivitas 8
Tujuan: siswa mengerjakan secara cepat soal-soal mengenai pecahan majemuk
Mengerjakan Latihan 6 dari buku Pecahan (buku 4)
Penjumlahan dan Pengurangan dengan Penyebut berbeda
Pada bagian ini kita akan melakukan operasi penjumlahan dan pengurangan dengan penyebut berbeda.
Penjumlahan Pecahan
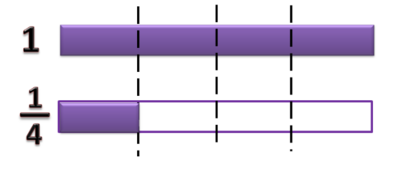
Bagaimana menghitung Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} + Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{3}} ?
- Disini penyebutnya berbeda.
- Kita harus ubah penyebutnya sehingga sama.
Bagaimana caranya?
Kita lihat konkretnya dulu
Ini ada batang Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} hendak ditambahkan dengan batang Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{3}} .
Agar kedua batang ini bisa dijumlahkan maka kelompoknya harus disamakan.
Cara menyamakan kelompok adalah sebagai berikut:
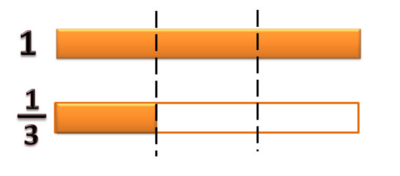
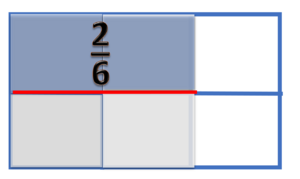
Pada pecahan Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} , tiap bagian kita potong menjadi 3 bagian yang identik. Sehingga kelompoknya menjadi kelompok 6.
Pada pecahan Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{3}} , tiap bagian kita potong menjadi 2 bagian yang identik. Sehingga kelompoknya menjadi kelompok 6.
Nah sekarang kedua pecahan mempunyai kelompok yang sama.
Secara abstrak ini dituliskan
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} dijadikan Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{3}{6}}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{3}} dijadikan Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{6}}
Sehingga kita peroleh
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} + Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{3}} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{3}{6}} + =
Cara Konkret lain adalah menggunakan Papan pecahan.
- Misal kita akan menghitung Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} + Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{3}} =
Ini adalah Papan pecahan.
Pertama kita lihat batang mana yang besarnya sama dengan batang Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}}
.
- Ternyata Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{4}} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{3}{6}} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{4}{8}} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{5}{10}} dst (bagian yang berwarna biru)
Kemudian kita lihat batang mana yang besarnya sama dengan batang Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{3}}
- Ternyata Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{3}} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{6}} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{3}{9}} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{4}{12}} dst (bagian yang berwarna merah)
Kita lihat mana penyebut yang sama dari kedua kelompok ini?
Jawabnya adalah 6.
Kita gabungkan kedua nilai pecahan diatas seperti pada gambar
Jadi Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} + Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{3}} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{5}{6}}
Cara lain (abstrak) mendapat penyebut 6 untuk soal di atas.
Cara termudah adalah
- Mengalikan penyebut pecahan yang dijumlahkan yaitu 3 x 2
Cara lain:
- Dengan mencari bilangan terkecil yang bisa dibagi 2 dan bisa dibagi 3.
Apakah penyebutnya boleh 12? Bukankah 12 juga bisa dibagi 2 atau dibagi 3?
- Boleh namun hasilnya nanti kamu harus sederhanakan lagi
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} + Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{3}} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{6}{12}} + Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{4}{12}} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{10}{12}} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{5}{6}}
Kita boleh mengubah pecahan menjadi 6, 12, 18, 24 dsb. Tetapi sebaiknya ambil yang terkecil yaitu 6.
Bagaimana menghitung Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{4}}
+ Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{6}}
= ?
- Kita ubah penyebutnya menjadi 4 x 6 = 24
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{4}} + Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{6}} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{6}{24}} + Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{4}{24}} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{10}{24}} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{5}{12}}
Atau
- cari bilangan yang bisa dibagi 4 dan 6. Dalam hal ini bilangannya adalah 12, 24, 36 dsb.
- Kita pilih bilangan yang terkecil yaitu 12.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{4}} + Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{6}} = + Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{12}} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{5}{12}}
Bagaimana dengan Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{5}} + Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{3}{10}} = ?
- kita ubah penyebutnya menjadi 5 x 10 = 50
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{5}} + = + = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{35}{50}} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{7}{10}}
Atau
- Cari bilangan yang bisa dibagi 5 dan bisa dibagi 10. Dalam hal ini bilangannya adalah 10, 20, 30, 40 dst..
- Kita pilih bilangan yang terkecil yaitu 10
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{5}} + Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{3}{10}} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{4}{10}} + Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{3}{10}} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{7}{10}}
Berikut ini adalah beberapa contoh penjumlahan pecahan
{{#ev:YouTube |id= 1iqMwdBkLf8 |width=640 |height=400 }}
1
Penjumlahan cepat
Perhatikan Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{5}} + Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{3}{10}} =
Penyebutnya dijadikan 5 x 10
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{lcl} \frac{2}{5} + \frac{3}{10} & = & \frac{2 \times 10}{5 \times 10} + \frac{3 \times 5}{10 \times 5} \\ & = & \frac{20}{50} + \frac{15}{50} \\ & = & \frac{35}{50} \\ & = & \frac{7}{10} \end{array} }
Lihat beberapa contoh berikut
a) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{4}{5}} + Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{3}} =
- Penyebutnya dijadikan 5 x 3
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{lcl} \frac{4}{5} + \frac{2}{3} & = & \frac{4 \times 3}{5 \times 3} + \frac{2 \times 5}{3 \times 5} \\ & = & \frac{12}{15} + \frac{10}{15} \\ & = & \frac{22}{15} \\ & = &1 \frac{7}{15} \end{array} }
b) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}}
+ Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{3}{4}}
=
- Penyebutnya dijadikan 2 x 4
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{lcl} \frac{1}{2} + \frac{3}{4} & = & \frac{1 \times 4}{2 \times 4} + \frac{3 \times 2}{4 \times 2} \\ & = & \frac{4}{8 } + \frac{6}{8 } \\ & = & \frac{10}{8} \\ & = & \frac{5}{4} \\ & = & 1\frac{1}{4} \end{array} }
c) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{3}}
+ Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{3}{5}}
=
- Penyebutnya dijadikan 3 x 5
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{lcl} \frac{1}{3} + \frac{3}{5} & = & \frac{1 \times 5}{3 \times 5} + \frac{3 \times 3}{5 \times 3} \\ & = & \frac{5}{15} +\frac{9}{15} \\ & = & \frac{14}{15} \end{array} }
d) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{5}}
+ Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{3}{7}}
=
- Penyebutnya dijadikan 5 x 7
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{lcl} \frac{2}{5} + \frac{3}{7} & = & \frac{2 \times 7}{5 \times 7} + \frac{3 \times 5}{7 \times 5} \\ & = & \frac{14}{35} +\frac{15}{35} \\ & = & \frac{29}{35} \end{array} }
Ada cara yang dilakukan orang untuk mempercepat perhitungan yaitu dengan pola perkalian silang. Namun di Gasing kami tidak terlalu merekomendasikan cara ini. Karena anak jadi kehilangan konsep menjumlah atau mengurangi pecahan. Yang diingat adalah rumus.
Video berikut ini menunjukan beberapa contoh menyelesaikan penjumlahan pecahan dengan cara cepat.
{{#ev:YouTube
|id= buzx2IqTY6o
|width=640
|height=400
}}
- Aktivitas 9
Tujuan: siswa mengerjakan secara cepat soal-soal mengenai penjumlahan pecahan dengan beda penyebut
Mengerjakan Latihan 11-12 dari buku Pecahan (buku 4)
Pengurangan Pecahan
Pengurangan pecahan dengan penyebut berbeda sama konsepnya dengan penjumlahan pecahan dengan penyebut berbeda.
Mereka yang sudah mahir penjumlahan pecahan akan sangat cepat mengerti pengurangan pecahan ini.
Misalnya bagaimana menghitung Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{4}} - Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{6}} = ?
- Kita ubah penyebutnya menjadi 4 x 6 = 24
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{4}} - = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{6}{24}} - Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{4}{24}} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{24}} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{12}}
Atau
- cari bilangan yang bisa dibagi 4 dan 6. Dalam hal ini bilangannya adalah 12, 24, 36 dsb.
- Kita pilih bilangan yang terkecil yaitu 12.
- - Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{6}} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{3}{12}} - = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{12}}
Bagaimana dengan Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{5}} - Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{3}{10}} = ?
- kita ubah penyebutnya menjadi 5 x 10 = 50
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{5}} - Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{3}{10}} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{20}{50}} - Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{15}{50}} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{5}{50}} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{10}}
Atau
- Cari bilangan yang bisa dibagi 5 dan bisa dibagi 10. Dalam hal ini bilangannya adalah 10, 20, 30, 40 dst..
- Kita pilih bilangan yang terkecil yaitu 10
- - Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{3}{10}} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{4}{10}} - Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{3}{10}} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{10}}
Lihat video cara mengerjakan pengurangan pecahan dengan penyebut berbeda
{{#ev:YouTube |id= 11fENTTJJ4o |width=640 |height=400 }}
Pengurangan cara cepat
Pola pengurangan pecahan cara cepat sama dengan pola penjumlahan pecahan cara cepat.
Perhatikan Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{5}} - Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{3}{10}} =
Penyebutnya dijadikan 5 x 10
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{lcl} \frac{2}{5} - \frac{3}{10} & = & \frac{2 \times 10}{5 \times 10} - \frac{3 \times 5}{10 \times 5} \\ & = & \frac{20}{50} -\frac{15}{50} \\ & = & \frac{5}{50} \\ & = & \frac{1}{10} \end{array} }
Bagaimana dengan Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{4}{5}}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{3}{7}}
= ?
- Penyebutnya dijadikan 5 x 7
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{lcl} \frac{4}{5} - \frac{3}{7} & = & \frac{4 \times 7}{5 \times 7} - \frac{3 \times 5}{7 \times 5} \\ & = & \frac{28}{35} -\frac{15}{35} \\ & = & \frac{13}{35} \end{array} }
Lihat video berikut ini untuk beberapa contoh pengurangan cara cepat
{{#ev:YouTube
|id= c3tZ95x8crc
|width=640
|height=400
}}
- Aktivitas 10
Tujuan: siswa mengerjakan secara cepat soal-soal mengenai penjumlahan pecahan dengan beda penyebut
Mengerjakan Latihan 15-16 dari buku Pecahan (buku 4)
Pecahan Negatif (cara cepat)
Konsep pecahan negatif, mirip dengan konsep bilangan bulat negatif.
Misalnya kita punya suatu garis bilangan. Tiap titik yang berdekatan berbeda Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{5}}
Dari titik 0 ke kanan, nilai tiap titik berturut-turut adalah dst.
Dari titik 0 ke kiri, nilai tiap titik berturut-turut adalah Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\frac{1}{5}, -\frac{2}{5}, -\frac{3}{5} } dst.
Operasi penjumlahan dan pengurangan bilangan pecahan negatif, adalah seperti operasi bilangan bulat negatif.
Berikut ini adalah beberapa contoh operasi bilangan pecahan negatif.
a) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\frac{4}{5}}
+ Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{3}{7}}
=
- Penyebutnya dijadikan 5 x 7
b) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\frac{4}{5}}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{3}{7}}
=
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{lcl} -\frac{4}{5} - \frac{3}{7} & = & \frac{-4 \times 7}{5 \times 7} - \frac{3 \times 5}{7 \times 5} \\ & = & \frac{-28}{35} -\frac{15}{35} \\ & = & \frac{-43}{35} \\ & = &- 1\frac{8}{35} \end{array} }
Beberapa contoh penjumlahan dan pengurangan bilangan pecahan negatif dapat dilihat dalam video ini
{{#ev:YouTube |id= VpMnTBKeF6c |width=640 |height=400 }}
Pecahan Biasa dan Pecahan Majemuk
Pecahan Biasa ke Pecahan Majemuk
Bagaimana menyederhanakan pecahan yang pembilangnya besar tetapi penyebutnya kecil seperti
- kita gunakan konsep pecahan dan bagi.
- 44 ÷ 7 = 6 sisa 2
- Hasil bilangan bulatnya kita ambil, dan sisanya kita jadikan pecahan Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{7}}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{44}{7}} = 6
Mari kita buktikan
- = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{42}{7}} + Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{7}}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{44}{7}} = 6 +
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{44}{7}} = 6 Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{7}}
Perhatikan beberapa contoh ini
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{43}{8} = ?}
- 43 ÷ 8 = 5 sisa 3
- = 5Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{3}{8}}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{25}{4} = ?}
- 25 ÷ 4 = 6 sisa 1
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{25}{4}} = 6
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{101}{9} = ?}
- 101 ÷ 9 = 11 sisa 2
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{101}{9}} = 11Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{9}}
Lihat beberapa contoh mengubah pecahan atau pecahan biasa menjadi pecahan majemuk dalam video berikut.
{{#ev:YouTube
|id= kXpA84IhSJk
|width=640
|height=400
}}
Pecahan Majemuk ke Pecahan Biasa
Bagaimana mengubah pecahan majemuk menjadi pecahan biasa atau pecahan murni?
Bagaimana mengubah 2 menjadi pecahan biasa?
Perhatikan langkah-langkahnya pada contoh berikut ini lalu lihat polanya dan buat kesimpulan
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{lcl} 3\frac{1}{3}& = & 3 + \frac{1}{3} \\ & = & \frac{9}{3} + \frac{1}{3} \\ & = & \frac{10}{3} \end{array} }
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{lcl} 5\frac{2}{7}& = & 5 + \frac{2}{7} \\ & = & \frac{35}{7} + \frac{2}{7} \\ & = & \frac{37}{7} \end{array} }
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{lcl} 4\frac{3}{5}& = & 4 + \frac{3}{5} \\ & = & \frac{20}{5} + \frac{3}{5} \\ & = & \frac{23}{5} \end{array} }
Video ini menunjukan contoh-contoh mengubah pecahan majemuk menjadi pecahan biasa.
{{#ev:YouTube |id= 49bF9cjeOY8 |width=640 |height=400 }}
- Aktivitas 11
Tujuan: siswa mengerjakan secara cepat soal-soal mengenai penjumlahan pecahan dengan beda penyebut
Mengerjakan Latihan 9 - 10 dari buku Pecahan (buku 4)
Titik Kritis
Titik Kritis untuk pecahan dicapai kalau siswa sudah mampu menguasai penjumlahan dan pengurangan seperti berikut ini
Model 1 : Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2 + \frac{5}{7} }
Penjumlahan bilangan bulat dengan pecahan dapat dilakukan sebagai berikut:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2 + \frac{5}{7} } = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2 \frac{5}{7} }
- = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 3 \frac{3}{10} }
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 7 + \frac{2}{9} } = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 7 \frac{2}{9} }
- =
Dapatkah Anda menemukan polanya?
Mudah kan?
{{#ev:YouTube
|id= _2gcqSKbjD0
|width=640
|height=400
}}
Model 2 : Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -2 - \frac{5}{7} }
Penjumlahan bilangan bulat dengan pecahan untuk model 2 ini mirip dengan model 1.
Perhatikan contoh berikut
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -2 - \frac{5}{7} } =
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -3 - \frac{3}{10} } = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -3 \frac{3}{10} }
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -7 - \frac{2}{9} } =
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -25 - \frac{5}{12} } = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -25 \frac{5}{12} }
Dapatkah Anda menemukan polanya?
Mudah kan?
{{#ev:YouTube
|id= 3C62l5SbC_M
|width=640
|height=400
}}
Model 3 :
Model 3 ini berbeda dengan model 1 dan 2.
- Langkah pertama adalah menghitung bentuk
- Cara mengerjakannya adalah mengubah 1 menjadi Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{7}{7} }
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1 - \frac{5}{7} } = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{7}{7} - \frac{5}{7} } =
Lihat beberapa contoh berikut
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1 - \frac{3}{11} } = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{11}{11} - \frac{3}{11} } = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{8}{11} }
- = = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{5} }
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1 - \frac{5}{8} } = = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{3}{8} }
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1 - \frac{4}{27} } = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{27}{27} - \frac{4}{27} } =
- Langkah kedua adalah memecah bilangan bulatnya menjadi 1 dan sisanya
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2 - \frac{5}{7} } = 1 + Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (1 - \frac{5}{7}) } = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1 + \frac{2}{7} } =
Perhatikan contoh berikutnya
- = 4 + = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 4 + \frac{2}{7} } = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 4 \frac{2}{7} }
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 7 - \frac{5}{7} } = 6 + Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (1 - \frac{5}{7}) } = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 6 + \frac{2}{7} } = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 6 \frac{2}{7} }
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 6 - \frac{5}{7} } = 5 + = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 5 + \frac{2}{7} } =
- = 22 + Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (1 - \frac{5}{7}) } = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 22 + \frac{2}{7} } = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 22 \frac{2}{7} }
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 5 - \frac{2}{9} } = 4 + = =
- = 6 + Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (1 - \frac{3}{11}) } = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 6 + \frac{8}{11} } =
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 6 - \frac{4}{5} } = 5 + Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (1 - \frac{4}{5}) } = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 5 + \frac{1}{5} } =
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 23 - \frac{7}{12} } = 22 + Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (1 - \frac{7}{12}) } = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 22 + \frac{5}{12} } =
Bisakah Anda melihat polanya?
{{#ev:YouTube |id= 77O3rzMluRQ |width=640 |height=400 }}
- Aktivitas 12
Tujuan: siswa mengerjakan secara cepat soal-soal mengenai model 3 titik kritis
Mengerjakan Latihan 15-18 dari buku Pecahan (buku 4)
Model 4 : Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -2 + \frac{5}{7} }
Model 4 ini berbeda dengan model sebelumnya.
- Langkah pertama adalah menghitung bentuk Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -1 + \frac{5}{7} }
- Cara mengerjakannya adalah mengubah -1 menjadi Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\frac{7}{7} }
- = = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\frac{2}{7} }
Lihat beberapa contoh berikut
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -1 + \frac{3}{11} } = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\frac{11}{11} + \frac{3}{11} } = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\frac{8}{11} }
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -1 + \frac{4}{5} } = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\frac{5}{5} + \frac{4}{5} } =
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -1 + \frac{5}{8} } = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\frac{8}{8} + \frac{5}{8} } =
- = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\frac{27}{27} + \frac{4}{27} } = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\frac{23}{27} }
- Langkah kedua adalah memecah bilangan bulatnya menjadi -1 dan sisanya
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -2 + \frac{5}{7} } = -1 + = = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -1 \frac{2}{7} }
Perhatikan contoh berikutnya
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -5 + \frac{5}{7} } = -4 Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (-1 + \frac{5}{7}) } = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -4 - \frac{2}{7} } = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -4 \frac{2}{7} }
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -7 + \frac{5}{7} } = -6 = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -6 -\frac{2}{7} } = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -6 \frac{2}{7} }
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -6 + \frac{5}{7} } = -5 = = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -5 \frac{2}{7} }
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -23 + \frac{5}{7} } = -22 Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (-1 + \frac{5}{7}) } = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -22 - \frac{2}{7} } = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -22 \frac{2}{7} }
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -5 + \frac{2}{9} } = -4 = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -4 -\frac{7}{9} } = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -4 \frac{7}{9} }
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -7 + \frac{3}{11} } = -6 = =
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -6 + \frac{4}{5} } = -5 Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (-1 + \frac{4}{5}) } = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -5 - \frac{1}{5} } = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -5 \frac{1}{5} }
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -23 + \frac{7}{12} } = -22 Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (-1 + \frac{7}{12}) } = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -22 - \frac{5}{12} } = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -22 \frac{5}{12} }
Bisakah Anda melihat polanya?
{{#ev:YouTube |id= yxicBxkmBlw |width=640 |height=400 }}
- Aktivitas 13
Tujuan: siswa mengerjakan secara cepat soal-soal mengenai model 3 titik kritis
Mengerjakan Latihan 19-22g dari buku Pecahan (buku 4)
Penjumlahan dan Pengurangan Pecahan Majemuk
Pada bagian ini kita belajar bagaiman melakukan penjumlahan dan pengurangan pecahan majemuk.
Ada 4 macam jenis bentuk soal-soal penjumlahan dan pengurangan pecahan majemuk ini.
model 1 : Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2\frac{2}{5} + 3\frac{3}{7} }
Pada model ini Pecahan Majemuk positif ditambah Pecahan Majemuk positif.
Contoh :
- Langkah pertama: jumlahkan bilangan bulatnya
- 2 + 3 = 5
- Langkah kedua : jumlahkan pecahannya
- Langkah ketiga : Jumlahkan bilangan bulat dan hasil pecahan
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 5 + 1\frac{5}{56} } = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 6\frac{5}{56} }
Jadi
- = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 6\frac{5}{56} }
Dalam video ini terdapat beberapa contoh lain penjumlahan model 1 ini.
{{#ev:YouTube |id= bul1s5UjLsA |width=640 |height=400 }}
model 2 : Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -2\frac{2}{5} - 3\frac{3}{7} }
Pada model ini Pecahan Majemuk negatif ditambah Pecahan Majemuk negatif.
Contoh : Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -2 \frac{5}{7} - 3 \frac{3}{8} }
- Langkah pertama: jumlahkan bilangan bulatnya
- -2 - 3 = -5
- Langkah kedua : jumlahkan pecahannya (ingat
- Langkah ketiga : Jumlahkan bilangan bulat dan hasil pecahan
- = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle - 6\frac{5}{56} }
Jadi
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -2 \frac{5}{7} - 3 \frac{3}{8} } = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -6\frac{5}{56} }
Dalam video ini terdapat beberapa contoh lain penjumlahan model 2 ini.
{{#ev:YouTube |id= 0Kw7CmMXKoI |width=640 |height=400 }}
model 3 : Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2\frac{2}{5} - 3\frac{3}{7} }
Pada model ini Pecahan Majemuk positif dikurangi Pecahan Majemuk positif.
Contoh :
- Langkah pertama: kurangkan bilangan bulatnya
- 2 - 3 = -1
- Langkah kedua : kurangkan pecahannya
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{lcl} \frac{5}{7} - \frac{3}{8} & = & \frac{5 \times 8}{7 \times 8} - \frac{7 \times 3}{7 \times 8} \\ & = & \frac{40}{56} - \frac{21}{56} \\ & = & \frac{19}{56} \end{array} }
- Langkah ketiga : Jumlahkan bilangan bulat dan hasil pecahan
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -1 + \frac{19}{56} } = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\frac{37}{56} }
Jadi
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2 \frac{5}{7} - 3 \frac{3}{8} } =
Dalam video ini terdapat beberapa contoh lain penjumlahan model 3 ini.
{{#ev:YouTube
|id= bul1s5UjLsA
|width=640
|height=400
}}
model 4 : Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -2\frac{2}{5} + 3\frac{3}{7} }
Pada model ini Pecahan Majemuk negatif ditambah Pecahan Majemuk positif.
Contoh :
- Langkah pertama: jumlahkan bilangan bulatnya
- -2 + 3 = 1
- Langkah kedua : jumlahkan pecahannya (ingat
- Langkah ketiga : Jumlahkan bilangan bulat dan hasil pecahan
- = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{37}{56} }
Jadi
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -2 \frac{5}{7} + 3 \frac{3}{8} } =
Dalam video ini terdapat beberapa contoh lain penjumlahan model 4 ini.
{{#ev:YouTube |id= 0Kw7CmMXKoI |width=640 |height=400 }}
- Aktivitas 13
Tujuan: siswa mengerjakan secara cepat soal-soal mengenai penjumlahan bilangan pecahan majemuk.
Mengerjakan Latihan 23 dari buku Pecahan (buku 4)
Perkalian Pecahan
Pembahasan perkalian pecahan akan kita bagi dalam 4 bagian
- Perkalian bilangan bulat dengan pecahan
- Perkalian pecahan dengan bilangan bulat
- Perkalian pecahan dengan pecahan
- Perkalian pecahan majemuk
Bilangan Bulat x bilangan Pecahan
- Perkalian bilangan pecahan menggunakan dasar konsep perkalian bilangan bulat yang sudah dipelajari sebelumnya.
- Dalam perkalian bilangan bulat kita tentu masih ingat bahwa 3 x 2 artinya 3 kotak isi 2, yaitu konkretnya ada 3 kotak yang masing-masing isinya 2 benda.
- Jadi hasilnya (abstrak) adalah 3 x 2 = 3▢2 = = 2 + 2 + 2 = 6.
- Sekarang bagaimana dengan 2 x Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} ?
- 2 x Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} artinya 2 kotak isi Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}}
- Konkretnya ada 2 kotak yang masing-masing berisi benda.
Jadi, abstraknya adalah
- 2 x = 2▢Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} = + Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{2}} = 1
Begitu pula
- 3 x = 3▢Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} = + Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} + Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} =
Kongkretnya digambarkan sebagai 3 kotak masing-masing berisi
Lakukan kegiatan eksplorasi perkalian bilangan bulat dengan pecahan seperti di atas dengan berbagai soal sehingga siswa menemukan pola bagaimana mendapatkan hasilnya dengan cepat, yaitu dengan mengalikan bilangan bulat dengan pembilang.
- Contohnya
- 3 x Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{5}} = 3▢Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{5}} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{5}} + + Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{5}} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{3 \times 2}{5}} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{6}{5}}
- Cara cepat
Video berikut menunjukan beberapa contoh perkalian bilangan bulat dengan bilangan pecahan.
{{#ev:YouTube |id= NZqqy1RcQ30 |width=640 |height=400 }}
Bilangan Pecahan x Bilangan Bulat
- Bagaimana dengan perkalian bilangan pecahan dengan bilangan bulat seperti Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} x 6 ?
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} x 6 artinya Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} kotak isi 6.
- Jadi konkretnya ada 6 kue dalam suatu kotak lalu kita bagi kotak tersebut menjadi 2 bagian yang sama besar (sehingga banyaknya kue dalam tiap bagian sama). lalu kita hitung berapa isi 1 bagiannya itu.
- Hasilnya adalah 3
- Jadi Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} x 6 = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} ▢6 = 3
- Sekarang bagaimana dengan Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{3}} x 6 = ?
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{3}} x 6 artinya Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{3}} kotak isi 6, jadi konkretnya ada 6 kue dalam suatu kotak lalu kita bagi kotak tersebut menjadi 3 bagian yang sama besar (sehingga banyaknya kue dalam tiap bagian sama). Lalu kita hitung berapa isi satu bagian kotak itu?
- Hasilnya adalah 2
- Jadi Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{3}} x 6 = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{3}} ▢6 = 2
- Bagaimana dengan Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{3}} x 9 = ?
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{3}} x 9 artinya Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{3}} kotak isi 9, jadi konkretnya ada 9 kue dalam suatu kotak lalu kita bagi kotak tersebut menjadi 3 bagian yang sama besar (sehingga banyaknya kue dalam tiap bagian sama). Lalu kita hitung berapa isi satu bagian kotak itu?
- Hasilnya adalah 3
- Jadi Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{3}} x 9 = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{3}} ▢9 = 3
Perhatikan hasil-hasil yang kita peroleh
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} x 6 hasilnya sama dengan membayangkan 6÷2 yaitu 3
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{3}} x 6 hasilnya sama dengan membayangkan 6÷3 yaitu 2
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{3}} x 9 hasilnya sama dengan membayangkan 9÷3 yaitu 3
Kesimpulan apa yang kita peroleh?
Kita lihat bahwa perkalian pecahan dengan bilangan bulat sama dengan pembagian bilangan bulat itu dengan penyebut.
- Bagaimana dengan Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{3}} x 9 = ?
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{3}} x 9 artinya Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{3}} kotak isi 9, jadi konkretnya ada 9 benda dalam suatu kotak lalu kita bagi kotak tersebut menjadi 3 bagian yang sama besar (sehingga banyaknya kue dalam tiap bagian sama). Lalu kita hitung berapa isi dua bagian kotak itu?
- Hasilnya adalah 2 x 3 = 6 benda
Hasilnya dapat digambarkan sebagai berikut. Hasilnya adalah 6 kue yang ada dalam daerah yang diarsir.
Berikut ini beberapa contoh perkalian pecahan dengan bilangan bulat
- a) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{3}{4}} x 12 = ?
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{3}{4}} x 12 artinya Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{3}{4}} kotak isi 12, jadi konkretnya ada 12 benda dalam suatu kotak lalu kita bagi kotak tersebut menjadi 4 bagian yang sama besar (sehingga banyaknya kue dalam tiap bagian sama). Lalu kita hitung berapa isi tiga bagian kotak itu?
- Hasilnya adalah 3 x 3 = 9 benda
- b) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{5}{6}} x 30 = ?
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{5}{6}} x 30 artinya Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{5}{6}} kotak isi 30, jadi konkretnya ada 30 benda dalam suatu kotak lalu kita bagi kotak tersebut menjadi 6 bagian yang sama besar (sehingga banyaknya kue dalam tiap bagian sama). Lalu kita hitung berapa isi lima bagian kotak itu?
- Hasilnya adalah 5 x 5 = 25 benda
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{5}{6}} x 30 = 25
- c) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{5}{7}} x 49 = ?
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{5}{7}} x 49 artinya Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{5}{7}} kotak isi 49, jadi konkretnya ada 49 benda dalam suatu kotak lalu kita bagi kotak tersebut menjadi 7 bagian yang sama besar (sehingga banyaknya kue dalam tiap bagian sama). Lalu kita hitung berapa isi lima bagian kotak itu?
- Hasilnya adalah 7x 5 =35 benda
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{5}{7}} x 49 = 35
- d) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{7}{9}} x 18 = ?
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{7}{9}} x 18 artinya Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{7}{9}} kotak isi 18, jadi konkretnya ada 18 benda dalam suatu kotak lalu kita bagi kotak tersebut menjadi 9 bagian yang sama besar (sehingga banyaknya kue dalam tiap bagian sama). Lalu kita hitung berapa isi tujuh bagian kotak itu?
- Hasilnya adalah 2x7 = 14 benda
Video berikut menunjukan beberapa contoh perkalian bilangan pecahan dengan bilangan bulat.
{{#ev:YouTube
|id= M9OCkcDBPfc
|width=640
|height=400
}}
Pecahan x Pecahan
Pada bab ini kita akan belajar tentang perkalian pecahan biasa dengan pecahan biasa, seperti Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{5} \times \frac{3}{7}}
Kita akan gunakan papan pecahan sebagai alat bantu.
Misalkan kita akan menghitung Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} × Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}}
Ini adalah pecahan Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2} \times \frac{1}{2}}
artinya kotak isinya Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}}
- Jadi disini kotak Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} kita bagi menjadi dua bagian yang sama besar.
- Kita cari dipapan pecahan, pecahan mana yang besarnya Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} tetapi terbagi atas dua bagian.
- Jawabnya adalah pecahan
- Jadi kita lihat bahwa kalau Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} dibagi 2, hasilnya adalah Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{4}}
- Dengan demikian Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2} \times \frac{1}{2}} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{4} }
Perhatikan beberapa contoh berikut
- a) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2} \times \frac{1}{3}}
- Pertama kita buat dulu pecahan Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{3} }
- Kemudian pecahan tersebut dibagi menjadi dua bagian yang sama besar.
- Salah satu bagian ini nilainya adalah Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2} \times \frac{1}{3}}
- Kalau kita perhatikan pada gambar diatas Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2} \times \frac{1}{3}} adalah nilai satu bagian dari satu kelompok yang terdiri dari 6 bagian yang sama besar. Ini adalah definisi Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{6} }
- Sehingga bisa disimpulkan bahwa Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2} \times \frac{1}{3}} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{6} }
- b) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{3} \times \frac{1}{2}}
- Pertama kita buat dulu pecahan Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2} }
- Kemudian pecahan tersebut dibagi menjadi tiga bagian yang sama besar.
- Salah satu bagian ini nilainya adalah Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{3} \times \frac{1}{2}}
- Kalau kita perhatikan pada gambar diatas Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{3} \times \frac{1}{2}} adalah nilai satu bagian dari satu kelompok yang terdiri dari 6 bagian yang sama besar. Ini adalah definisi Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{6} }
- Sehingga bisa disimpulkan bahwa Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{3} \times \frac{1}{2}} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{6} }
- c)
- Pertama kita buat dulu pecahan Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{3} }
- Kemudian pecahan tersebut dibagi menjadi dua bagian yang sama besar.
- Salah satu bagian ini nilainya adalah Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2} \times \frac{2}{3}}
- Kalau kita perhatikan pada gambar diatas Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2} \times \frac{2}{3}} adalah nilai dua bagian dari satu kelompok yang terdiri dari 6 bagian yang sama besar. Ini adalah definisi Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{6} }
- Sehingga bisa disimpulkan bahwa Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2} \times \frac{2}{3}} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{6} }
Lakukan eksplorasi ini berulang-ulang, sampai siswa melihat pola bahwa pada perkalian pecahan dengan pecahan, maka hasilnya diperoleh dengan mengalikan pembilang dengan pembilang dan penyebut dengan penyebut.
Perhatikan contoh beberapa perkalian pecahan dibawah ini
- a) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{3} \times \frac{3}{5}} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2 \times 3}{3 \times 5} } = = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{5} }
- b) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{5}{7} \times \frac{7}{9}} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{5 \times 7}{7 \times 9} } = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{35}{63} } = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{5}{9} }
Cara coret:
Ada kalanya dalam perkalian pecahan kita bisa lakukan cara cepat yaitu dengan membagi pembilang dan penyebut dengan bilangan tertentu sebelum mereka dikalikan.
Perhatikan contoh berikut
- a) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{3} \times \frac{3}{5}}
- Langkah pertama adalah mengalikan pembilang dengan pembilang dan penyebut dengan penyebut
- = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2 \times 3}{3 \times 5} }
- Langkah kedua adalah membagi pembilang dan penyebut dengan 3.
- Pembilang 3 ÷ 3 = 1
- Penyebut 3 ÷ 3 = 1
- Langkah ketiga adalah kalikan pembilang dengan pembilang dan penyebut dengan penyebut
- Pembilang 2 x 1 = 2
- Penyebut 1 x 5 = 5
- Hasilnya adalah
Kalau sudah mahir kita bisa coret diawal seperti pada gambar ini.
- Pembilang 2 x 1 = 2
- Penyebut 1 x 5 = 5
- Hasilnya Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{5} }
- b) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{5}{7} \times \frac{7}{9}}
- Langkah pertama adalah mengalikan pembilang dengan pembilang dan penyebut dengan penyebut
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{5}{7} \times \frac{7}{9}} =
- Langkah kedua adalah membagi pembilang dan penyebut dengan 7.
- Pembilang 7÷7 = 1
- Penyebut 7÷7 = 1
- Langkah ketiga adalah kalikan pembilang dengan pembilang dan penyebut dengan penyebut
- Pembilang 5 x 1 = 5
- Penyebut 1 x 9 = 9
- Hasilnya adalah Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{5}{9} }
Kalau sudah mahir kita bisa coret diawal seperti pada gambar ini.
- Pembilang 5 x 1 = 5
- Penyebut 1 x 9 = 9
- Hasilnya
- c) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{16}{15} \times \frac{9}{4}}
Kita bisa selesaikan soal ini dengan mengalikan pembilang dengan pembilang dan penyebut dengan penyebut. Kemudian kita sederhanakan seperti ditunjukan pada gambar ini.
Atau kita melakukan penyederhanaan diawal pembilang dan penyebut dibagi dengan bilangan yang sama.
- 16 ÷ 4 = 4 (pembilang) dan 4 ÷ 4 = 1 (penyebut)
- 15 ÷ 3 = 5 (penyebut) dan 9:3 = 3 (pembilang)
Kemudian mengalikan pembilang dengan pembilang dan penyebut dengan penyebut
- Pembilang = 4 x 3 = 12
- Penyebut = 5 x 1 = 5
Video berikut ini beberapa contoh perkalian pecahan dengan pecahan
{{#ev:YouTube
|id= xDjEDKLGLys
|width=640
|height=400
}}
- Aktivitas 14
Tujuan: siswa mengerjakan secara cepat soal-soal mengenai perkalian pecahan
Mengerjakan Latihan 24-26 dari buku Pecahan (buku 4)
Pecahan Majemuk x Pecahan Majemuk
Pada perkalian pecahan majemuk, kita harus mengubah dulu pecahan majemuk ini menjadi pecahan biasa. Setelah itu kita bisa lakukan perkalian pecahan seperti yang sudah dipelajari sebelumnya.
Perhatikan contoh berikut
- a) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2 \frac{4}{7} \times 3\frac{2}{4}} =
Hasil perhitungan diberikan pada gambar dibawah ini
- b) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 3 \frac{3}{7} \times 2\frac{12}{15}} =
Hasil perhitungan diberikan pada gambar dibawah ini
- c) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1 \frac{4}{8} \times 3\frac{7}{14}} =
Hasil perhitungan dapat dilihat pada gambar dibawah ini
Pada soal diatas kita bisa juga menyederhanakan pecahan lebih awal lagi
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{4}{8} = \frac{1}{2}}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{7}{14} = \frac{1}{2}}
Hasilnya adalah
Video berikut ini memberikan beberapa variasi soal perkalian pecahan majemuk
{{#ev:YouTube |id= Z9I-h-4lcRU |width=640 |height=400 }}
- Aktivitas 15
Tujuan: siswa mengerjakan secara cepat soal-soal mengenai perkalian pecahan majemuk
Mengerjakan Latihan 27 dari buku Pecahan (buku 4)
Perkalian 3 Pecahan
Pada perkalian 3 pecahan kita bisa lakukan dengan sistem coret.
Untuk lebih jelasnya lihat video berikut ini.
{{#ev:YouTube
|id= 3v2nL6veuZ0
|width=640
|height=400
}}
- Aktivitas 16
Tujuan: siswa mengerjakan secara cepat soal-soal mengenai perkalian pecahan majemuk
Mengerjakan Latihan 28 dari buku Pecahan (buku 4)
Pembagian Pecahan
Pembahasan pembagian pecahan akan kita bagi dalam 4 bagian
- Pembagian bilangan bulat dengan pecahan
- Pembagian pecahan dengan bilangan bulat
- Pembagian pecahan dengan pecahan
- Pembagian pecahan majemuk
Bilangan Pecahan ÷ Bilangan Bulat
- Pembagian pecahan menggunakan dasar konsep pembagian yang sudah dipelajari sebelumnya.
- Dalam pembagian kita tentu masih ingat bahwa 6 ÷ 2 artinya saya punya 6 benda hendak dimasukan dalam 2 kotak, berapa yang diterima tiap kotak.
- Kita sudah tahu bahwa jawabnya adalah 3 benda.
- Bagaimana dengan pembagian bilangan pecahan dengan bilangan bulat seperti Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} ÷ 2 ?
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} ÷ 2 artinya kue hendak dimasukan dalam 2 kotak. Berapa isi masing-masing kotak agar pembagian ini adil dan merata.
Yang kita perlu lakukan adalah membagi dua kue Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} itu. Kemudian memasukan tiap bagian ke dalam kotak. Kita lihat tiap kotak akan menerima masing-masing Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{4}} kue.
Dengan demikian Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} ÷ 2 = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{4}}
- Sekarang bagaimana dengan Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{3}} : 2 = ?
Kita bisa gunakan papan pecahan.
Ini pecahan Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{3}}
Cari di papan pecahan, pecahan yang nilainya Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{3}} tapi terbagi 2.
Jawabnya adalah pada gambar ini
Disini terlihat bahwa Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{3} : 2 = \frac{1}{6} }
- Bagaimana dengan Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} ÷ 5 = ?
Kita bisa gunakan papan pecahan.
Ini pecahan Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}}
Cari di papan pecahan, pecahan yang nilainya Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} tapi terbagi 5.
Jawabnya adalah pada gambar ini
Disini terlihat bahwa
Perhatikan hasil-hasil yang kita peroleh dibawah ini
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} ÷ 6, kita membayangkan 1/2 kue dipotong-potong jadi 6 bagian yang sama hasilnya yaitu Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{12}}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{3}} ÷ 4, kita membayangkan 1/3 kue dipotong-potong jadi 4 bagian yang sama hasilnya yaitu Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{12}}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{5}} ÷ 7, kita membayangkan 1/5 kue dipotong-potong menjadi 7 bagian yang sama hasilnya yaitu Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{35}}
Video berikut menunjukan beberapa contoh perkalian bilangan pecahan dengan bilangan bulat.
{{#ev:YouTube |id= DBSXhkjXA7o |width=640 |height=400 }}
Bilangan Bulat ÷ Bilangan Pecahan
- Kalimat perkalian 2 x 3 = 6, artinya jika ada 2 kotak masing-masing kotak isi 3 benda maka jumlah seluruh benda dalam kotak-kotak itu adalah 6 benda.
- Dari perkalian 2 x 3 = 6, maka arti pembagian 6:2 = 3 adalah kita punya 6 benda hendak dibagikan dalam 2 kotak, maka isi tiap kotak adalah 3 benda.
- Dari perkalian 2 x 3 = 6, maka arti pembagian 6:3 = 2 adalah kita punya 6 benda hendak dimasukan dalam kotak, setiap kotak hanya bisa menampung 3 benda, maka jumlah kotak yang bisa menerima 6 benda ini ada 2 kotak.
Disini kita lihat ada 2 arti pembagian. Pembagian pertama yang sering kita pakai adalah menanyakan isi kotak. Sedangkan pembagian kedua adalah menanyakan banyak kotak.
Untuk perkalian bilangan bulat x bilangan pecahan, kita akan gunakan arti pembagian kedua.
Contoh: 1÷ Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} = ? Untuk melihat konkretnya ada baiknya kita ambil wadah air 1 liter dan wadah air 1/2 liter. Air dituang dari wadah 1 liter ke wadah 1/2 liter... kita lihat bahwa kita membutuhkan 2 wadah yang 1/2 liter.
Jadi 1÷ Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} = 2
- Bagaimana dengan pembagian 1 ÷ Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} ?
- Saya punya kue hendak dimasukan dalam kotak dengan kapasitas atau ukuran Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} , berapa banyak potong kue dapat dimasukan dalam kotak tersebut?
Gambar dibawah ini menggambarkan situasi ketika 1 potong kue sudah masuk kotak pertama.
Ini gambar situasi ketika 2 potong kue sudah masuk kotak kedua.
Jadi jumlah kotak yang dibutuhkan adalah 2 kotak.
Sekarang kita akan hitung 1 ÷ Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{4}}
- Pada gambar diatas kita punya 1 kue, hendak kita masukan dalam beberapa kotak dengan kapasitas atau ukuran .
- Kue kita bagi menjadi potongan Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{4}} agar bisa masuk kotak.
- Kita lihat bahwa banyak kotak adalah 4 buah.
Jadi
- 1 ÷ Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{4}} = 4
Bisa juga kita gunakan wadah 1 liter dan wadah 1/4 liter. Air dalam wadah 1 liter kita tuangkan dalam wadah 1/4 liter dan kita bisa lihat bahwa untuk ini dibutuhkan 4 wadah. Jadi
1 ÷ Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{4}} = 4
Dengan cara yang sama kita bisa dapatkan bahwa
- 1 ÷ Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{3}} = 3
- 1 ÷ Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{6}} = 6
- 1 ÷ Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{10}} = 10
Pola apa yang Anda lihat?
- Bagaimana kalau 2 ÷ Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} = ?
- Karena
- 1 ÷ Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} = 2
- maka
- 2 ÷ = 2 x 2 = 4
Dengan cara yang sama kita bisa peroleh
- 2 ÷ = 2 x 3 = 6
- 2 ÷ Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{4}} = 2 x 4 = 8
- 2 ÷ = 2 x 6 = 12
- 2 ÷ Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{10}} = 2 x 10 = 20
Dan dengan pola yang sama kita bisa peroleh
- 5 ÷ Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{3}} = 5 x 3 = 15
- 9 ÷ Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{4}} = 9 x 4 = 36
- 12 ÷ Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{6}} = 12 x 6 = 72
- 25 ÷ = 25 x 10 = 250
Jadi resep untuk menghitung perbagian bilangan bulat dengan bilangan pecahan seperti 25 ÷ Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{10}}
adalah dengan membayangkan 1 kali÷ Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{10}}
. Kemudian hasilnya ini dikalikan 25. Hasilnya adalah 250.
Video berikut menunjukan berbagai contoh pembagian bilangan bulat dengan pecahan.
{{#ev:YouTube |id= RbJ0IYVfnss |width=640 |height=400 }}
Pecahan ÷ Pecahan
Pada bagian ini kita akan belajar tentang pembagian pecahan biasa dengan pecahan biasa, seperti Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{5} \div \frac{3}{7}}
Misalkan kita akan menghitung Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}}
÷ Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{4}}
artinya ada kue berukuran Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} hendak dimasukan dalam kotak berukuran Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{4}} , ada berapa banyak kotak dibutuhkan?
Kue berukuran Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}}
tidak bisa masuk kedalam kotak berukuran Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{4}}
. Karena itu maka kue Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}}
harus dipotong menjadi beberapa potongan kue berukuran Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{4}}
.
Kita lihat pada gambar bahwa kue Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} bisa dipotong menjadi 2 kue berukuran Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{4}} .
Kue yang sudah dipotong ini dimasukan satu persatu ke dalam kotak Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{4}} .
Banyak kotak yang dibutuhkan adalah 2 buah.
- Dengan demikian Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2} \div \frac{1}{4}} = 2
Kita bisa juga lakukan ini dengan wadah 1/2 liter air dan wadah 1/4 liter air. Kita masukan air dari wadah 1/2 liter ke wadah 1/4 liter. Kita lihat bahwa kita butuh 2 wadah. Jadi
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2} \div \frac{1}{4}} = 2
Sekarang kita gunakan papan pecahan untuk menjelaskan soal diatas.
Ini adalah pecahan Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2} \div \frac{1}{4}} artinya ada batang Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} hendak dimasukan dalam kotak Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{4}} , ada berapa buah kotak dibutuhkan.
Pecahan Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} terlalu besar untuk masuk kotak Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{4}} . Karena itu maka pecahan Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} itu harus dipotong menjadi beberapa potongan pecahan Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{4}} .
Kita lihat pada gambar bahwa pecahan Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} bisa dipotong menjadi 2 buah pecahan Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{4}} .
Potongan pecahan Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{4}} ini \kemudian dimasukan satu persatu ke dalam kotak Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{4}} .
Banyak kotak yang dibutuhkan adalah 2 buah.
- Dengan demikian Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2} \div \frac{1}{4}} = 2
Perhatikan beberapa contoh berikut
- a) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2} \div \frac{1}{8}}
- Arti Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2} \div \frac{1}{8}} adalah kita mempunyai pecahan Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2} }
hendak dimasukan dalam kotak berukuran Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{8} } , tentunya pecahan itu harus dipotong-potong. Ada berapa kotak dibutuhkan?
- Cari di papan pecahan, pecahan
- Tempatkan pecahan Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2} } ini ke dalam deretan pecahan Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{8}} . Kita lihat
ada 4 pecahan Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{8}} yang nilainya Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2} } . Dengan kata lain ada 4 kotak Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{8}} dibutuhkan untuk menampung Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2} } .