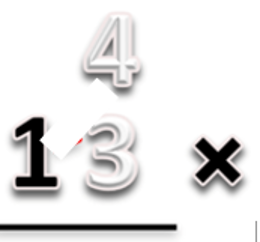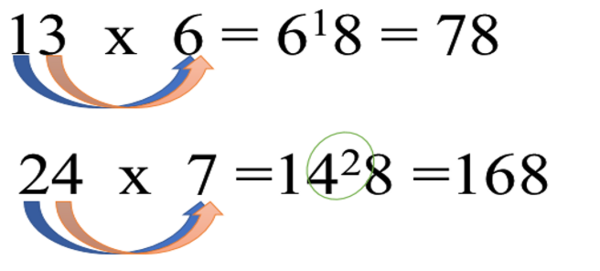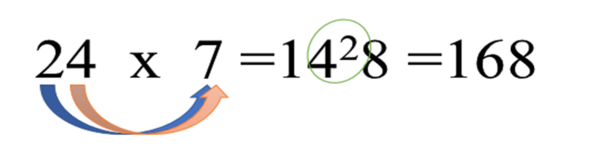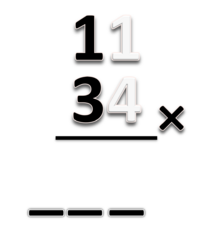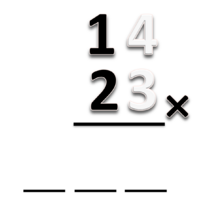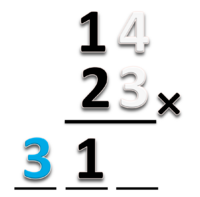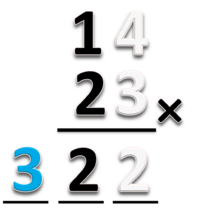Difference between revisions of "GABER Perkalian"
m (Text replacement - "{{#ev:youtube|hP3ENPc8Jf0 |width=900 |height=500 }} " to "{{#widget:YouTube |id= hP3ENPc8Jf0 |width= 900 |height=500 }}") |
|||
| Line 8: | Line 8: | ||
{{#widget:YouTube | {{#widget:YouTube | ||
|id=fZV5z97hi1Q | |id=fZV5z97hi1Q | ||
|width=900 | |{{#widget:YouTube | ||
|id= hP3ENPc8Jf0 | |||
|width= 900 | |||
|height=500 | |height=500 | ||
}}|height=500 | |||
}} | }} | ||
| Line 40: | Line 43: | ||
{{#widget:YouTube | {{#widget:YouTube | ||
|id=aTVse3idRo4 | |id=aTVse3idRo4 | ||
|width=900 | |{{#widget:YouTube | ||
|id= hP3ENPc8Jf0 | |||
|width= 900 | |||
|height=500 | |height=500 | ||
}}|height=500 | |||
}} | }} | ||
== Konsep Perkalian == | == Konsep Perkalian == | ||
| Line 109: | Line 115: | ||
{{#widget:YouTube | {{#widget:YouTube | ||
|id=fnkP2udP_Qc | |id=fnkP2udP_Qc | ||
|width=900 | |{{#widget:YouTube | ||
|id= hP3ENPc8Jf0 | |||
|width= 900 | |||
|height=500 | |height=500 | ||
}}|height=500 | |||
}} | }} | ||
| Line 413: | Line 422: | ||
{{#widget:YouTube | {{#widget:YouTube | ||
|id=ueP6Xo5eMQo | |id=ueP6Xo5eMQo | ||
|width=900 | |{{#widget:YouTube | ||
|id= hP3ENPc8Jf0 | |||
|width= 900 | |||
|height=500 | |height=500 | ||
}}|height=500 | |||
}} | }} | ||
| Line 495: | Line 507: | ||
{{#widget:YouTube | {{#widget:YouTube | ||
|id=zeuJfXM_hyU | |id=zeuJfXM_hyU | ||
|width=900 | |{{#widget:YouTube | ||
|id= hP3ENPc8Jf0 | |||
|width= 900 | |||
|height=500 | |height=500 | ||
}}|height=500 | |||
|start=12 | |start=12 | ||
|end=70 | |end=70 | ||
| Line 1,194: | Line 1,209: | ||
{{#widget:YouTube | {{#widget:YouTube | ||
|id=WrOcPfuI1v8 | |id=WrOcPfuI1v8 | ||
|width=900 | |{{#widget:YouTube | ||
|id= hP3ENPc8Jf0 | |||
|width= 900 | |||
|height=500 | |height=500 | ||
}}|height=500 | |||
}} | }} | ||
| Line 1,367: | Line 1,385: | ||
{{#widget:YouTube | {{#widget:YouTube | ||
|id=Y8T4M0JpwZ0 | |id=Y8T4M0JpwZ0 | ||
|width=900 | |{{#widget:YouTube | ||
|id= hP3ENPc8Jf0 | |||
|width= 900 | |||
|height=500 | |height=500 | ||
}}|height=500 | |||
}} | }} | ||
| Line 1,706: | Line 1,727: | ||
{{#widget:YouTube | {{#widget:YouTube | ||
|id=s5HrmJCjSwg | |id=s5HrmJCjSwg | ||
|width=900 | |{{#widget:YouTube | ||
|id= hP3ENPc8Jf0 | |||
|width= 900 | |||
|height=500 | |height=500 | ||
}}|height=500 | |||
}} | }} | ||
| Line 1,715: | Line 1,739: | ||
{{#widget:YouTube | {{#widget:YouTube | ||
|id=aTVse3idRo4 | |id=aTVse3idRo4 | ||
|width=900 | |{{#widget:YouTube | ||
|id= hP3ENPc8Jf0 | |||
|width= 900 | |||
|height=500 | |height=500 | ||
}}|height=500 | |||
}} | }} | ||
| Line 1,886: | Line 1,913: | ||
{{#widget:YouTube | {{#widget:YouTube | ||
|id=EwDxjm6PAeg | |id=EwDxjm6PAeg | ||
|width=900 | |{{#widget:YouTube | ||
|id= hP3ENPc8Jf0 | |||
|width= 900 | |||
|height=500 | |height=500 | ||
}}|height=500 | |||
}} | }} | ||
| Line 2,032: | Line 2,062: | ||
{{#widget:YouTube | {{#widget:YouTube | ||
|id=t630efAuHPU | |id=t630efAuHPU | ||
|width=900 | |{{#widget:YouTube | ||
|id= hP3ENPc8Jf0 | |||
|width= 900 | |||
|height=500 | |height=500 | ||
}}|height=500 | |||
}} | }} | ||
| Line 2,043: | Line 2,076: | ||
{{#widget:YouTube | {{#widget:YouTube | ||
|id=otJTJfb0ybI | |id=otJTJfb0ybI | ||
|width=900 | |{{#widget:YouTube | ||
|id= hP3ENPc8Jf0 | |||
|width= 900 | |||
|height=500 | |height=500 | ||
}}|height=500 | |||
}} | }} | ||
| Line 2,055: | Line 2,091: | ||
{{#widget:YouTube | {{#widget:YouTube | ||
|id=t60Xf_PTwX0 | |id=t60Xf_PTwX0 | ||
|width=900 | |{{#widget:YouTube | ||
|id= hP3ENPc8Jf0 | |||
|width= 900 | |||
|height=500 | |height=500 | ||
}}|height=500 | |||
}} | }} | ||
| Line 2,353: | Line 2,392: | ||
{{#widget:YouTube | {{#widget:YouTube | ||
|id=WjlqJ4_xtSE | |id=WjlqJ4_xtSE | ||
|width=900 | |{{#widget:YouTube | ||
|id= hP3ENPc8Jf0 | |||
|width= 900 | |||
|height=500 | |height=500 | ||
}}|height=500 | |||
}} | }} | ||
| Line 2,363: | Line 2,405: | ||
{{#widget:YouTube | {{#widget:YouTube | ||
|id=tr0mVI82Z2U | |id=tr0mVI82Z2U | ||
|width=900 | |{{#widget:YouTube | ||
|id= hP3ENPc8Jf0 | |||
|width= 900 | |||
|height=500 | |height=500 | ||
}}|height=500 | |||
}} | }} | ||
| Line 2,485: | Line 2,530: | ||
{{#widget:YouTube | {{#widget:YouTube | ||
|id=66h-vtR4v-g | |id=66h-vtR4v-g | ||
|width=900 | |{{#widget:YouTube | ||
|id= hP3ENPc8Jf0 | |||
|width= 900 | |||
|height=500 | |height=500 | ||
}}|height=500 | |||
}} | }} | ||
| Line 2,495: | Line 2,543: | ||
{{#widget:YouTube | {{#widget:YouTube | ||
|id=lu32xELbprk | |id=lu32xELbprk | ||
|width=900 | |{{#widget:YouTube | ||
|id= hP3ENPc8Jf0 | |||
|width= 900 | |||
|height=500 | |height=500 | ||
}}|height=500 | |||
}} | }} | ||
| Line 2,505: | Line 2,556: | ||
{{#widget:YouTube | {{#widget:YouTube | ||
|id=wFRzC8fHCnc | |id=wFRzC8fHCnc | ||
|width=900 | |{{#widget:YouTube | ||
|id= hP3ENPc8Jf0 | |||
|width= 900 | |||
|height=500 | |height=500 | ||
}}|height=500 | |||
}} | }} | ||
| Line 2,514: | Line 2,568: | ||
{{#widget:YouTube | {{#widget:YouTube | ||
|id=WM9_EWxMmRU | |id=WM9_EWxMmRU | ||
|width=900 | |{{#widget:YouTube | ||
|id= hP3ENPc8Jf0 | |||
|width= 900 | |||
|height=500 | |height=500 | ||
}}|height=500 | |||
}} | }} | ||
| Line 2,523: | Line 2,580: | ||
{{#widget:YouTube | {{#widget:YouTube | ||
|id=2YjohymcuKQ | |id=2YjohymcuKQ | ||
|width=900 | |{{#widget:YouTube | ||
|id= hP3ENPc8Jf0 | |||
|width= 900 | |||
|height=500 | |height=500 | ||
}}|height=500 | |||
}} | }} | ||
| Line 2,533: | Line 2,593: | ||
{{#widget:YouTube | {{#widget:YouTube | ||
|id=Jcj4Pw6fBr8 | |id=Jcj4Pw6fBr8 | ||
|width=900 | |{{#widget:YouTube | ||
|id= hP3ENPc8Jf0 | |||
|width= 900 | |||
|height=500 | |height=500 | ||
}}|height=500 | |||
}} | }} | ||
| Line 2,545: | Line 2,608: | ||
{{#widget:YouTube | {{#widget:YouTube | ||
|id=qHgodm1L34c | |id=qHgodm1L34c | ||
|width=900 | |{{#widget:YouTube | ||
|id= hP3ENPc8Jf0 | |||
|width= 900 | |||
|height=500 | |height=500 | ||
}}|height=500 | |||
}} | }} | ||
| Line 2,554: | Line 2,620: | ||
{{#widget:YouTube | {{#widget:YouTube | ||
|id=Nk2GQcs9rsY | |id=Nk2GQcs9rsY | ||
|width=900 | |{{#widget:YouTube | ||
|id= hP3ENPc8Jf0 | |||
|width= 900 | |||
|height=500 | |height=500 | ||
}}|height=500 | |||
}} | }} | ||
Revision as of 05:46, 13 January 2024
Perkalian Sudah di edit
GASING Berhitung : Perkalian
Pada pelajaran perkalian ini siswa diharapkan mampu secara cepat menghitung berbagai jenis perkalian bilangan satu angka sampai bilangan tiga angka. Siswa diharapkan bisa mencongak perkalian bilangan dua angka dengan bilangan dua angka.
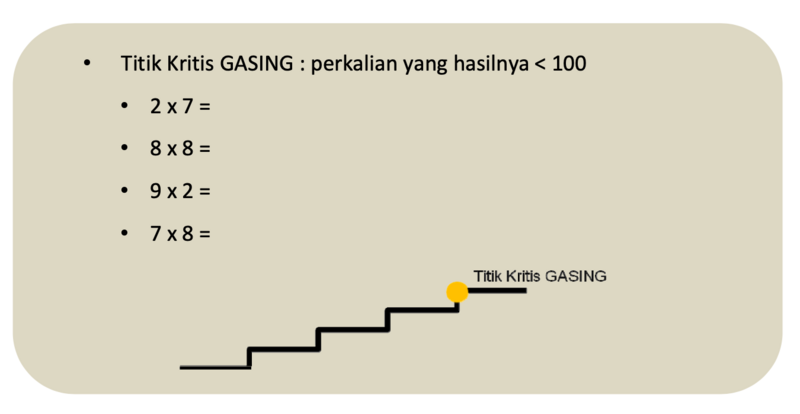
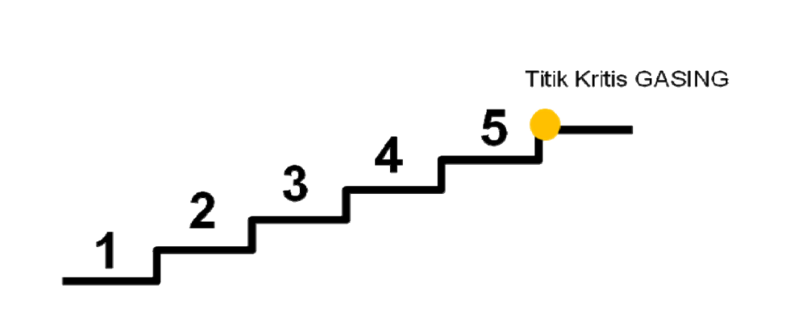
- Titik Kritis Gasing Perkalian
Titik kritis Gasing perkalian adalah penguasaan perkalian bilangan satu angka dengan bilangan satu angka. Artinya kalau siswa sudah lewat titik kritis gasing ini maka siswa akan mampu menghitung perkalian bilangan berapa angka pun.
Ada beberapa tahapan untuk mencapai titik kritis perkalian yaitu:
- Konsep perkalian
- Perkalian 1,10, 9, 2, dan 5
- Perkalian Bilangan yang Sama
- Perkalian 3,4
- Perkalian 8,7,6
Mengapa tidak berurutan dari 1 sampai 10?
Dalam metode gasing kita memulai berhitung dari yang paling mudah.
Jika kita mengikuti tahapan-tahapan ini maka siswa bisa belajar dengan sangat mudah dan lebih cepat menguasai perkalian bilangan 1 angka ini.
Ini video siswa yang sudah lewat titik kritis Perkalian.
Konsep Perkalian
Sekarang kita masuk ke tahap pertama yaitu konsep perkalian.
- 1. Kenalkan media yang akan digunakan seperti kotak dan benda konkret yang dapat diisi dalam kotak.
- 2. Dalam menjelaskan konsep perkalian perlu diperhatikan bahwa media kotak yang digunakan sudah diisi benda konkret
Perhatikan ilustrasi di bawah ini:
- Ini ada 2 kotak masing-masing kotak berisi 5 nanas
- Simbolnya 2 ▢5 (dibaca: 2 kotak dimana 1 kotaknya berisi 5 benda, yang selanjutnya kalimatnya disederhanakan menjadi 2 kotak masing-masing berisi 5)
- 2 ▢5 sering dikenal dengan 2 x 5
- 2 x 5 artinya apa? Artinya adalah 2 ▢5 (dibaca 2 kotak masing-masing berisi 5).
- berapa hasil dari 2 x 5 =? Hasilnya adalah kita menghitung jumlah seluruh benda dalam seluruh kotak yaitu 5(isi kotak pertama) + 5 (isi kotak kedua) = 10 (dalam hal ini 10 nanas)
- Jadi 2 x 5 = 2 ▢5 = 5 + 5 = 10
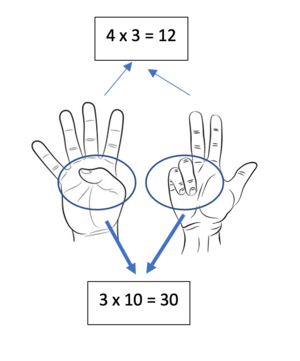
- Ini ada 3 kotak masing-masing kotak berisi 4 rambutan
- Simbolnya 3 ▢4 (dibaca: 3 kotak masing-masing berisi 4)
- 3 ▢4 sering dikenal dengan 3 x 4
- 3 x 4 artinya apa? Artinya adalah 3 ▢4 (dibaca 3 kotak masing-masing berisi 4).
- berapa hasil dari 3 x 4 =? Hasilnya adalah kita menghitung jumlah seluruh benda dalam seluruh kotak yaitu 4(isi kotak pertama) + 4 (isi kotak kedua) + 4 (isi kotak ketiga) = 12 (dalam hal ini 12 rambutan)
- Jadi 3 x 4 = 3 ▢4 = 4 + 4 + 4 = 12
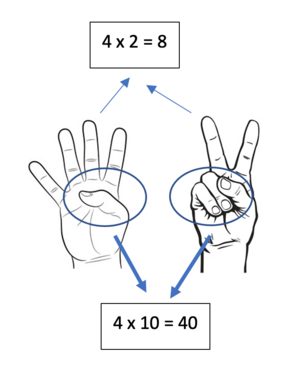
- Ini ada 4 kotak masing-masing kotak berisi 2 kelereng
- Simbolnya 4 ▢4 (dibaca: 4 kotak masing-masing berisi 2)
- 4 ▢2 sering dikenal dengan 4 x 2
- 4 x 2 artinya apa? Artinya adalah 4 ▢2 (dibaca 4 kotak masing-masing berisi 2).
- berapa hasil dari 4 x 2 =? Hasilnya adalah kita menghitung jumlah seluruh benda dalam seluruh kotak yaitu 2(isi kotak pertama) + 2 (isi kotak kedua) + 2 (isi kotak ketiga) + 2 (isi kotak keempat) = 8 (dalam hal ini 8 kelereng)
- Jadi 4 x 2 = 4 ▢2 = 2 + 2 + 2 + 2 = 8
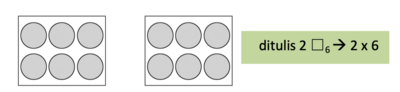
Untuk gambar ini kita boleh menulis " Jadi 2 x 6 = 2 ▢6 = 6 + 6 = 12 (dibaca 2 x 6 artinya 2 kotak masing-masing berisi 6 benda sama dengan 6 + 6 sama dengan 12).
Selanjutnya perhatikan bahwa
- 4 x 2 = 4 ▢2 = 2 + 2 + 2 + 2 = 8
- dan
- 2 x 4 = 2 ▢4 = 4 + 4 = 8
Keduanya bernilai sama.
- Kita boleh tulis 4 x 2 = 2 x 4
- Perhatikan disini 4 x 2 = 8 nilainya sama dengan 2 x 4 = 8
- (Kesimpulannya adalah 4 x 2 dengan 2 x 4 nilainya sama akan tetapi artinya berbeda).
Ini video seorang guru yang melakukan micro teaching tentang konsep perkalian.
Perkalian 1, 10, 9, 2 dan 5
Pada bagian ini kita akan memanfaatkan pola bilangan atau berbagai alat peraga sederhana untuk lebih mudah mengerti dan mencongak perkalian bilangan-bilangan ini.
Kita akan bagi tahapan-tahapan ini menjadi 5 bagian
- Perkalian 1
- Perkalian 10
- Perkalian 9
- Perkalian 2
- Perkalian 5
Perkalian 1
- 1. Kita memulai dari tahap konkret yaitu dengan menyiapkan media kotak dan benda konkretnya
- 2. Dalam perkalian 1 atau perkalian dengan bilangan 1 masing-masing kotak berisi 1 benda konkret.
- 3. Dimulai dari menjelaskan konkret 1x1
- a. Tunjukkan 1 kotak berisi 1 benda konkret (misalnya benda konkretnya adalah stik)
- b. Berikut contoh dialognya:
- Guru : G dan Siswa : S
- G : Anak-anak, coba lihat ibu guru memegang apa?
- S : Kotak, Bu
- G : Ada berapa kotak, dan apakah isi kotaknya?
- S : Ada 1 kotak berisi 1 stik
- G : 1 kotak berisi 1 stik simbolnya 1 ▢1 atau biasa kita kenal dengan 1 x 1.
Sekarang ibu guru mau bertanya, apakah arti 1x1?
- S : 1 ▢1 (dibaca satu kotak berisi 1 stik).
- G : Nah, hasilnya adalah kita menghitung jumlah isi semua kotak. Maka berapakah
hasil dari 1x1?
- S : satu…
- G : Betul… 1x1 sama dengan 1.
- c. Guru menuliskan seperti berikut ini:
KONKRET
- 1 ▢1 = 1 x 1
- 1 x 1 = 1 ▢1 = 1
Untuk selanjutnya guru menjelaskan konkret dari 2 x 1 sampai 10 x 1 seperti langkah pada poin 3b. Kemudian menuliskannya seperti berikut ini!
- 2 x 1 = 2 ▢1 = 1 + 1 = 2
- 3 x 1 = 3 ▢1 = 1 + 1 + 1 = 3
- 4 x 1 = 4 ▢1 = 1 + 1 + 1 + 1 = 4
- 5 x 1 = 5 ▢1 = 1 + 1 + 1 + 1 + 1 = 5
- 6 x 1 = 6 ▢1 = 1 + 1 + 1 + 1 + 1 + 1 = 6
- 7 x 1 = 7 ▢1 = 1 + 1 + 1 + 1 + 1 + 1 + 1 = 7
- 8 x 1 = 8 ▢1 = 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 = 8
- 9 x 1 = 9 ▢1 = 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 = 9
- 10 x 1 = 10 ▢1 = 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 = 10
Selanjutnya kita masuk tahap abstrak dengan menuliskan perkalian dan hasilnya seperti berikut ini:
ABSTRAK
- 1 x 1 = 1
- 2 x 1 = 2
- 3 x 1 = 3
- 4 x 1 = 4
- 5 x 1 = 5
- 6 x 1 = 6
- 7 x 1 = 7
- 8 x 1 = 8
- 9 x 1 = 9
- 10 x 1 = 10
Ini adalah bentuk abstrak dari perkalian 1.
MENCONGAK
Dalam gasing setelah konkret dan abstrak langkah selanjutnya adalah mencongak.
konkret → abstrak → mencongak
- Bagaimana mencongak perkalian 1?
- Dengan melihat pola.
- Apa pola hasil perkalian 1 diatas?
Polanya adalah perkalian suatu bilangan dengan bilangan 1 menghasilkan bilangan itu sendiri.😁👏
- [ 1 ] x 1 = [ 1 ]
- [ 2 ] x 1 = [ 2 ]
- [ 3 ] x 1 = [ 3 ]
- [ 4 ] x 1 = [ 4 ]
- [ 5 ] x 1 = [ 5 ]
- [ 6 ] x 1 = [ 6 ]
- [ 7 ] x 1 = [ 7 ]
- [ 8 ] x 1 = [ 8 ]
- [ 9 ] x 1 = [ 9 ]
- [ 10 ] x 1 = [ 10 ]
- Jadi sekarang kita bisa dengan mudah menghitung 156 x 1 = ?. Hasilnya adalah berupa bilangan itu sendiri yaitu 156.
- Catatan: disini kita menggunakan istilah mencongak bukan menghafal. Mencongak tidak sekedar menghafal. Mencongak adalah suatu proses berpikir. Mencongak bisa menjawab kenapa, tidak sekedar tahu hasilnya saja.
- Activitas 1a
Tujuan: melatih kemampuan mencongak siswa untuk perkalian 1
Siswa dilatih mencongak perkalian 1 minimal 1 menit.
- Aktivitas 1b: siswa mengerjakan secara cepat perkalian 1
Tujuan: siswa mampu mengerjakan Perkalian Latihan 1.
Ajak siswa berlatih dengan latihan berikut:
Latihan Perkalian Latihan 1.
Tujuan: siswa mengerjakan secara cepat perkalian 1
Mengerjakan Latihan 1 dari buku Perkalian
Perkalian 10
- 1. Kita memulai dari tahap konkret yaitu dengan menyiapkan media kotak dan benda konkretnya
- 2. Dalam perkalian 10 atau perkalian dengan bilangan 10 masing-masing kotak berisi 10 benda konkret.
- 3. Dimulai dari menjelaskan konkret 1x10
- a. Tunjukkan 1 kotak berisi 10 benda konkret (misalnya benda konkretnya adalah sedotan)
- b. Berikut contoh dialognya:
- Guru : G dan Siswa : S
- G : Anak-anak, coba lihat ibu guru memegang apa?
- S : Kotak, Bu
- G : Ada berapa kotak, dan apakah isi kotaknya?
- S : Ada 1 kotak berisi 10 Sedotan
- G : 1 kotak berisi 10 sedotan simbolnya 1 ▢10 atau biasa kita kenal dengan 1 x 10.
Sekarang ibu guru mau bertanya, apakah arti 1x10?
- S : 1 ▢10 (dibaca satu kotak berisi 10 sedotan).
- G : Nah, hasilnya adalah kita menghitung jumlah benda dalam semua kotak. Maka berapakah
hasil dari 1x10?
- S : sepuluh…
- G : Betul… 1x10 sama dengan 10.
- c. Guru menuliskan seperti berikut ini:
KONKRET
- 1 ▢10 = 1 x 10
- 1 x 10 = 1 ▢10 = 10
Untuk selanjutnya guru menjelaskan konkret dari 2 x 10 sampai 10 x 10 seperti langkah pada poin 3b. Kemudian menuliskannya seperti berikut ini!
- 2 x 10 = 2 ▢10 = 10 + 10 = 20
- 3 x 10 = 3 ▢10 = 10 + 10 + 10 = 30
- 4 x 10 = 4 ▢10 = 10 + 10 + 10 + 10 = 40
- 5 x 10 = 5 ▢10 = 10 + 10 + 10 + 10 + 10 = 50
- 6 x 10 = 6 ▢10 = 10 + 10 + 10 + 10 + 10 + 10 = 60
- 7 x 10 = 7 ▢10 = 10 + 10 + 10 + 10 + 10 + 10 + 10 = 70
- 8 x 10 = 8 ▢10 = 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 = 80
- 9 x 10 = 9 ▢10 = 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 = 90
- 10 x 10 = 10 ▢10 = 10 + 10 + 10 + 10 + 10 + 10 +10 + 10 + 10 + 10 + 10 = 100
Selanjutnya kita masuk tahap abstrak dengan menuliskan perkalian dan hasilnya seperti berikut ini:
ABSTRAK
- 1 x 10 = 10
- 2 x 10 = 20
- 3 x 10 = 30
- 4 x 10 = 40
- 5 x 10 = 50
- 6 x 10 = 60
- 7 x 10 = 70
- 8 x 10 = 80
- 9 x 10 = 90
- 10 x 10 = 100
Ini adalah bentuk abstrak dari perkalian 10.
MENCONGAK
Dalam gasing setelah konkret dan abstrak langkah selanjutnya adalah mencongak.
konkret → abstrak → mencongak
- Bagaimana mencongak perkalian 10?
- Dengan melihat pola.
- Apa pola hasil perkalian 10 diatas?
Polanya adalah perkalian suatu bilangan dengan 10 menghasilkan bilangan itu sendiri ditambahkan bulatan dibelakangnya (orang sebut bulatan ini sebagai angka nol, tapi sementara kita sebut sebagai bulat saja) .😁👏
- [ 1 ] x 10 = [ 1 ] 0
- [ 2 ] x 10 = [ 2 ] 0
- [ 3 ] x 10 = [ 3 ] 0
- [ 4 ] x 10 = [ 4 ] 0
- [ 5 ] x 10 = [ 5 ] 0
- [ 6 ] x 10 = [ 6 ] 0
- [ 7 ] x 10 = [ 7 ] 0
- [ 8 ] x 10 = [ 8 ] 0
- [ 9 ] x 10 = [ 9 ] 0
- [ 10 ] x 10 = [ 10 ] 0
Jadi kita bisa menghitung 345 x 10 = ? , yaitu 3450 (hanya menambahkan 0 dibelakang 345). Mudah kan?
- Activitas 1c
Tujuan: melatih kemampuan mencongak siswa untuk perkalian 10
Siswa mencongak perkalian 10 secara cepat.
- Aktivitas 1d: siswa mengerjakan secara cepat perkalian 10
Tujuan: siswa mampu mengerjakan Perkalian Latihan 10.
Ajak siswa berlatih dengan latihan berikut:
Latihan Perkalian Latihan 10.
Perkalian 9
- 1. Kita memulai dari tahap konkret yaitu dengan menyiapkan media kotak dan benda konkretnya
- 2. Dalam perkalian 9 atau perkalian dengan bilangan 9 masing-masing kotak berisi 9 benda konkret.
- 3. Dimulai dari menjelaskan konkret 1x9
- a. Tunjukkan 1 kotak berisi 9 benda konkret (misalnya benda konkretnya adalah pulpen)
- b. Berikut contoh dialognya:
- Guru : G dan Siswa : S
- G : Anak-anak, coba lihat ibu guru memegang apa?
- S : Kotak, Bu
- G : Ada berapa kotak, dan apakah isi kotaknya?
- S : Ada 1 kotak berisi 9 pulpen
- G : 1 kotak berisi 19 pulpen simbolnya 1 ▢9 atau biasa kita kenal dengan 1 x 9.
Sekarang ibu guru mau bertanya, apakah arti 1x9?
- S : 1 ▢9 (dibaca satu kotak berisi 9 pulpen).
- G : Nah, hasilnya adalah kita menghitung jumlah benda dalam semua kotak. Maka berapakah
hasil dari 1x9?
- S : sembilan…
- G : Betul… 1x9 sama dengan 9.
- c. Guru menuliskan seperti berikut ini:
KONKRET
- 1 ▢9 = 1 x 9
- 1 x 9 = 1 ▢9 = 9
Untuk selanjutnya guru menjelaskan konkret dari 2 x 9 sampai 10 x 9 seperti langkah pada poin 3b. Kemudian menuliskannya seperti berikut ini!
- 2 x 9 = 2 ▢9 = 9 + 9 = 18
- 3 x 9 = 3 ▢9 = 9 + 9 + 9 = 27
- 4 x 9 = 4 ▢9 = 9 + 9 + 9 + 9 = 36
- 5 x 9 = 5 ▢9 = 9 + 9 + 9 + 9 + 9 = 45
- 6 x 9 = 6 ▢9 = 9 + 9 + 9 + 9 + 9 + 9 = 54
- 7 x 9 = 7 ▢9 = 9 + 9 + 9 + 9 + 9 + 9 + 9 = 63
- 8 x 9 = 8 ▢9 = 9 + 9 + 9 + 9 + 9 + 9 + 9 + 9 = 72
- 9 x 9 = 9 ▢9 = 9 + 9 + 9 + 9 + 9 + 9 + 9 + 9 + 9 = 81
- 10 x 9 = 10 ▢9 = 9 + 9 + 9 + 9 + 9 + 9 +9 + 9 + 9 + 9 + 9 = 90
Dalam menghitung penjumlahan 9 seperti 9 + 9 + 9 + 9 kita menggunakan sistem coret seperti yang pernah dipelajari dalam Penjumlahan banyak bilangan satu angka.
Selanjutnya kita masuk tahap abstrak dengan menuliskan perkalian dan hasilnya seperti berikut ini:
ABSTRAK
- 1 x 9 = 9
- 2 x 9 = 18
- 3 x 9 = 27
- 4 x 9 = 36
- 5 x 9 = 45
- 6 x 9 = 54
- 7 x 9 = 63
- 8 x 9 = 72
- 9 x 9 = 81
- 10 x 9 = 90
Ini adalah bentuk abstrak dari perkalian 9.
MENCONGAK
Dalam gasing setelah konkret dan abstrak langkah selanjutnya adalah mencongak.
konkret → abstrak → mencongak
- Bagaimana mencongak perkalian 9?
- Dengan melihat pola.
- Apa pola hasil perkalian 9 diatas?
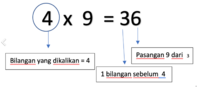
Pola pertama, digambarkan pada gambar di bawah ini.
- Misalnya kita hendak menghitung 4 x 9 =
- Disini bilangan yang hendak dikalikan adalah 4
- Hasilnya terdiri dari bilangan 2 angka.
- Angka pertama adalah 1 bilangan sebelum bilangan yang dikalikan (dalam barisan bilangan asli)
- Dalam hal ini angka pertama adalah 1 bilangan sebelum 4 yaitu 3
- Angka kedua adalah pasangan 9 dari angka pertama yaitu 6 (didapat dari 3 tambah berapa jadi 6). Pasangan 9 ini sudah dipelajari dalam bab penjumlahan
Dengan pola ini mencongak perkalian 9 dapat dilakukan dengan cepat (asalkan penjumlahan 9 sudah dikuasai dengan baik).
- 1 x 9 = 9
- [ 2 ] x 9 = < 1 > 8
- [ 3 ] x 9 = < 2 > 7
- [ 4 ] x 9 = < 3 > 6
- [ 5 ] x 9 = < 4 > 5
- [ 6 ] x 9 = < 5 > 4
- [ 7 ] x 9 = < 6 > 3
- [ 8 ] x 9 = < 7 > 2
- [ 9 ] x 9 = < 8 > 1
- 10 x 9 = 90
- catatan: 1 x 9 dan 10 x 9 sudah dihitung pada perkalian 1 dan perkalian 10 karena 1 x 9 = 9 x 1 dan 10 x 9 = 9 x 10. Yang perlu dipelajari khusus adalah perkalian 2 x9 sampai 9 x 9.
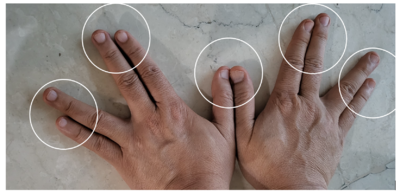
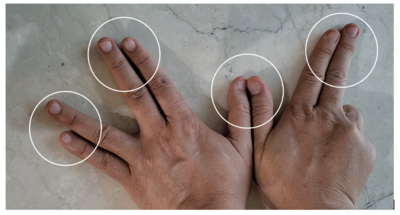
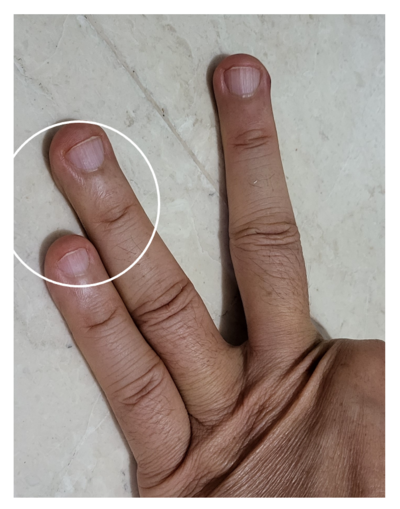
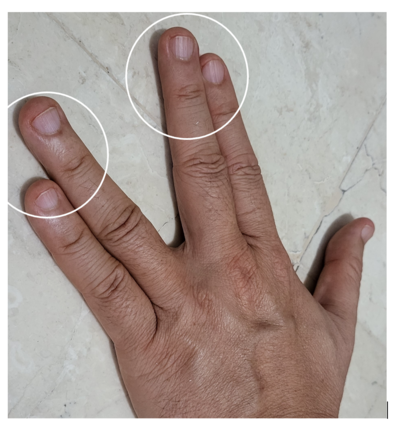
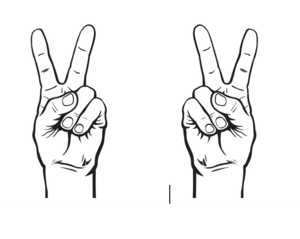
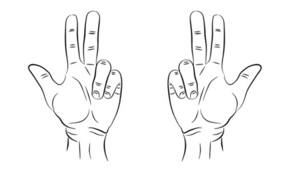
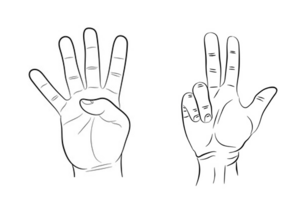
Pola kedua adalah dengan menggunakan jari
- Namakan jari dari 1 sampai 10 seperti pada gambar
- Untuk menghitung 2 x 9 tekuk jari nomor 2.
- Jumlah jari disebelah kiri jari yang ditekuk adalah 1
- Jumlah jari disebelah kanan jari yang ditekuk adalah 8
- Jadi 2 x 9 adalah 18
- Untuk menghitung 4 x 9 tekuk jari nomor 4.
- Jumlah jari disebelah kiri jari yang ditekuk adalah 3
- Jumlah jari disebelah kanan jari yang ditekuk adalah 6
- Jadi 4 x 9 adalah 36
Cara ini bisa dikombinasikan dengan lagu perkalian 9 seperti pada video berikut:
Lagu perkalian 9
- Perkalian 9 (lagu balonku)
- Jariku ada spuluh
- Berguna untuk hitung
- Hitung kali Sembilan
- Jadi mudah sekali
- Tekuk jari kedua hasilnya dlapan belas
- Tekuk jari ketiga hasilnya dua tujuh
- Tekuk jari keempat hasilnya tiga enam
- Tekuk jari kelima hasilnya empat lima
- Tekuk jari keenam hasilnya lima empat
- Tekuk jari ketujuh hasilnya enam tiga
- Tekuk jari kedlapan duarrr hasilnya tujuh dua
- Tekuk jari Sembilan hasilnya delapan satu.
- Activitas 1e
Tujuan: melatih kemampuan mencongak siswa untuk perkalian 9
Siswa mencongak perkalian 9 secara cepat.
- Aktivitas 1f: Mengerjakan secara cepat perkalian 9
Tujuan: siswa mampu mengerjakan secara cepat perkalian 9
Ajak siswa berlatih dengan latihan berikut:
Latihan perkalian 9
Perkalian 2
- 1. Kita memulai dari tahap konkret yaitu dengan menyiapkan media kotak dan benda konkretnya
- 2. Dalam perkalian 2 atau perkalian dengan bilangan 2 masing-masing kotak berisi 2 benda konkret.
- 3. Dimulai dari menjelaskan konkret 1x2. Untuk perkalian 1 x 2 konsepnya sama seperti sebelumnya. Berikut ini adalah contoh cara menjelaskan konkret untuk 3 x 3.
- a. Tunjukkan 3 kotak berisi 2 benda konkret (misalnya benda konkretnya adalah penghapus)
- b. Berikut contoh dialognya:
- Guru : G dan Siswa : S
- G : Anak-anak, coba lihat ibu guru memegang apa?
- S : Kotak, Bu
- G : Ada berapa kotak, dan apakah isi kotaknya?
- S : Ada 3 kotak masing-masing kotak berisi 2 penghapus
- G : 3 kotak berisi 2 penghapus simbolnya 3 ▢2 atau biasa kita kenal dengan 3 x 2.
Sekarang ibu guru mau bertanya, apakah arti 3x2?
- S : 3 ▢2 (dibaca tiga kotak berisi 2 penghapus).
- G : Nah, hasilnya adalah kita menghitung jumlah benda dalam semua kotak. Maka berapakah
hasil dari 3x2? Mari kita menghitung bersama..
- G + S : 2 dikota pertama + 2 di kotak kedua + 2 di kotak ketiga, jumlah semua bendanya ada 6.
- G : Betul… 3x2 sama dengan 6.
- c. Guru menuliskan seperti berikut ini:
KONKRET
- 1 ▢2 = 1 x 2
- 1 x 2 = 1 ▢2 = 2
Untuk selanjutnya guru menjelaskan konkret dari 2 x 2 sampai 10 x 2 seperti langkah pada poin 3b. Kemudian menuliskannya seperti berikut ini!
- 2 x 2 = 2 ▢2 = 2 + 2 = 4
- 3 x 2 = 3 ▢2 = 2 + 2 + 2 = 6
- 4 x 2 = 4 ▢2 = 2 + 2 + 2 + 2 = 8
- 5 x 2 = 5 ▢2 = 2 + 2 + 2 + 2 + 2 = 10
- 6 x 2 = 6 ▢2 = 2 + 2 + 2 + 2 + 2 + 2 = 12
- 7 x 2 = 7 ▢2 = 2 + 2 + 2 + 2 + 2 + 2 + 2 = 14
- 8 x 2 = 8 ▢2 = 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 = 16
- 9 x 2 = 9 ▢2 = 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 = 18
- 10 x 2 = 10 ▢2 = 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 = 20
Selanjutnya kita masuk tahap abstrak dengan menuliskan perkalian dan hasilnya seperti berikut ini:
ABSTRAK
- 1 x 2 = 2
- 2 x 2 = 4
- 3 x 2 = 6
- 4 x 2 = 8
- 5 x 2 = 10
- 6 x 2 = 12
- 7 x 2 = 14
- 8 x 2 = 16
- 9 x 2 = 18
- 10 x 2 = 20
MENCONGAK
Dalam gasing setelah konkret dan abstrak langkah selanjutnya adalah mencongak.
konkret → abstrak → mencongak
- Bagaimana mencongak perkalian 2?
- Dengan melihat pola.
- Apa pola hasil perkalian 2 diatas?
Inilah pola perkalian 2!
- Hasil perkalian suatu bilangan dengan bilangan 2 sama nilainya dengan menjumlahkan bilangan tsb dengan dirinya sendiri. (catatan : Pola tidak sama dengan arti perkalian, maksudnya adalah 4 x 2 kalau pakai pola hasilnya adalah 4 + 4. Sedangkan kalau pakai arti perkalian hasilnya adalah 4 x 2 = 2 + 2 + 2 + 2).
- 1 x 2 = 2
- 2 x 2 = 2 + 2 = 4
- 3 x 2 = 3 + 3 = 6
- 4 x 2 = 4 + 4 = 8
- 5 x 2 = 5 + 5 = 10
- 6 x 2 = 6 + 6 = 12
- 7 x 2 = 7 + 7 = 14
- 8 x 2 = 8 + 8 = 16
- 9 x 2 = 18
- 10 x 2 = 20
Catatan: Perkalian 1 x 2, 10 x 2 dan 9 x 2 sudah dipelajari diperkalian 1, 10 dan 9. Sehingga untuk perkalian 2 ini yang dicongak adalah 2 x 2 sampai 8 x 2.
- Activitas 1g
Tujuan: melatih kemampuan mencongak siswa untuk perkalian 2
Siswa mencongak perkalian 2 secara cepat.
- Activitas 1h
Tujuan: siswa mengerjakan secara cepat perkalian 2
Ajak siswa berlatih dengan latihan berikut:
Latihan perkalian 2
Perkalian 5
- 1. Kita memulai dari tahap konkret yaitu dengan menyiapkan media kotak dan benda konkretnya
- 2. Dalam perkalian 5 atau perkalian dengan bilangan 5 masing-masing kotak berisi 5 benda konkret.
- 3. Dimulai dari menjelaskan konkret 1x2. Untuk perkalian 1x5 konsepnya sama seperti sebelumnya. Berikut ini adalah contoh cara menjelaskan konkret untuk 4 x 5.
- a. Tunjukkan 4 kotak berisi 5 benda konkret (misalnya benda konkretnya adalah kelereng)
- b. Berikut contoh dialognya:
- Guru : G dan Siswa : S
- G : Anak-anak, coba lihat ibu guru memegang apa?
- S : Kotak, Bu
- G : Ada berapa kotak, dan apakah isi kotaknya?
- S : Ada 4 kotak masing-masing kotak berisi 5 kelereng
- G : 4 kotak berisi 5 kelereng simbolnya 4 ▢5 atau biasa kita kenal dengan 4 x 5.
Sekarang ibu guru mau bertanya, apakah arti 4x5?
- S : 4 ▢5 (dibaca empat kotak berisi 5 kelereng ).
- G : Nah, hasilnya adalah kita menghitung jumlah benda dalam semua kotak. Maka berapakah
hasil dari 4x5? Mari kita menghitung bersama..
- G + S : 5 dikotak pertama + 5 di kotak kedua + 5 di kotak ketiga + 5 di kotak keempat sama dengan 20.
- G : Betul… 4 x 5 sama dengan 20.
- c. Guru menuliskan seperti berikut ini:
KONKRET
- 1 ▢5 = 1 x 5
- 1 x 5 = 1 ▢5 = 5
Untuk selanjutnya guru menjelaskan konkret dari 1 x 5 sampai 10 x 5 seperti langkah pada poin 3b. Kemudian menuliskannya seperti berikut ini!
- 2 x 5 = 2 ▢5 = 5 + 5 = 10
- 3 x 5 = 3 ▢5 = 5 + 5 + 5 = 15
- 4 x 5 = 4 ▢5 = 5 + 5 + 5 + 5 = 20
- 5 x 5 = 5 ▢5 = 5 + 5 + 5 + 5 + 5 = 25
- 6 x 5 = 6 ▢5 = 5 + 5 + 5 + 5 + 5 + 5 = 30
- 7 x 5 = 7 ▢5 = 5 + 5 + 5 + 5 + 5 + 5 + 5 = 35
- 8 x 5 = 8 ▢5 = 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 = 40
- 9 x 5 = 9 ▢5 = 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 = 45
- 10 x 5 = 10 ▢5 = 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 = 50
Selanjutnya kita masuk tahap abstrak dengan menuliskan perkalian dan hasilnya seperti berikut ini:
ABSTRAK
- 1 x 5 = 5
- 2 x 5 = 10
- 3 x 5 = 15
- 4 x 5 = 20
- 5 x 5 = 25
- 6 x 5 = 30
- 7 x 5 = 35
- 8 x 5 = 40
- 9 x 5 = 45
- 10 x 5 = 50
MENCONGAK
Dalam gasing setelah konkret dan abstrak langkah selanjutnya adalah mencongak.
konkret → abstrak → mencongak
- Bagaimana mencongak perkalian 5?
- Dengan melihat pola.
- Apa pola hasil perkalian 5 diatas?
- 1 x 5 = 5
- 2 x 5 = 10
- 3 x 5 = 15
- 4 x 5 = 20 👈
- 5 x 5 = 25
- 6 x 5 = 30 👈
- 7 x 5 = 35
- 8 x 5 = 40 👈
- 9 x 5 = 45
- 10 x 5 = 50
Kita fokus pada 4 x 5, 6 x 5 dan 8 x 5 dulu.
Kita gunakan jari kita.
Kelompokan jari kita menjadi kelompok yang terdiri dari 2 jari.
Untuk 4 x 5
- Tunjukan 4 jari.
- Tiap jari bernilai 5. Dua jari bernilai 10
- 4 Jari terdiri dari 2 kelompok 2 jari, nilainya 10 + 10 = 20
- jadi 4 x 5 = 20
Untuk 6 x 5
- Tunjukan 6 jari.
- Tiap jari bernilai 5. Dua jari bernilai 10
- 6 Jari terdiri dari 3 kelompok 2 jari, nilainya 10 + 10 + 10 = 30
- jadi 6 x 5 = 30
Untuk 8 x 5
- Tunjukan 8 jari.
- Tiap jari bernilai 5. Dua jari bernilai 10
- 8 Jari terdiri dari 3 kelompok 2 jari, nilainya 10 + 10 + 10 + 10 = 40
- jadi 8 x 5 = 40
Latih ini berulang-ulang sampai siswa hafal.
Sekarang kita fokus pada 3 x 5, 5 x 5, 7 x 5
- 1 x 5 = 5
- 2 x 5 = 10
- 3 x 5 = 15
- 4 x 5 = 20
- 5 x 5 = 25
- 6 x 5 = 30
- 7 x 5 = 35
- 8 x 5 = 40
- 9 x 5 = 45
- 10 x 5 = 50
Kita gunakan jari lagi.
Untuk 3 x 5
- Tunjukan 3 jari.
- Tiap jari bernilai 5. Dua jari bernilai 10
- 3 Jari terdiri dari 1 kelompok 2 jari, dan 1 kelompok 1 jari, nilainya 10 + 5 = 15
- jadi 3 x 5 = 15
Untuk 5 x 5
- Tunjukan 5 jari.
- Tiap jari bernilai 5. Dua jari bernilai 10
- 5 Jari terdiri dari 2 kelompok 2 jari, dan 1 kelompok 1 jari, nilainya 20 + 5 = 25
- jadi 5 x 5 = 25
Lakukan ini untuk 7 x 5 juga.
Lakukan ini berulang-ulang sampai mahir.
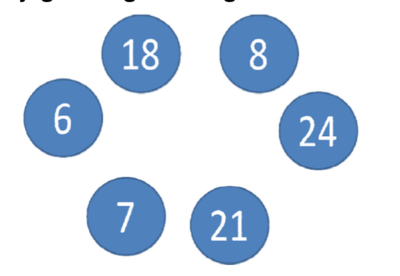
- Aktivitas 1i bermain dalam lingkaran
Tujuan: membantu anak mencongak 6 x 5, 7 x 5 dan 8 x 5.
- Jumlah siswa 4-5 orang
- Buat lingkaran dengan tulisan 30, 35, dan 40
- Saat bilangan 8 disebutkan maka siswa masuk ke dalam lingkaran 40
- Saat bilangan 7 disebutkan maka siswa masuk ke dalam lingkaran 35
- Saat bilangan 6 disebutkan maka siswa masuk ke dalam lingkaran 30
Lakukan ini berulang-ulang.
- Ini bisa divariasi dengan menunjuk 1 siswa masuk ke suatu lingkaran sambil berteriak perkalian yang hasilnya ada dalam lingkaran itu.
- Misalnya kita minta siswa masuk ke lingkaran 35, maka siswa harus berteriak 7 x 5 = 35
Lakukan ini berulang-ulang.
- Activitas 1j
Tujuan: melatih kemampuan mencongak siswa untuk perkalian 5
Siswa mencongak perkalian 5 secara cepat.
- Activitas 1k
Tujuan: siswa mengerjakan secara cepat perkalian 5
Ajak siswa berlatih dengan latihan berikut:
Latihan perkalian 5
Perkalian Bilangan yang Sama
Tahap berikutnya adalah perkalian dengan bilangan yang sama atau kuadrat bilangan misalnya 3 x 3 bisa juga disebut 3^2 (dibaca 3 pangkat 2 atau 3 kuadrat). Adapun langkah untuk menjelaskan konkret, abstrak, mencongak dari perkalian bilangan yang sama adalah :
- 1. Kita memulai dari tahap konkret yaitu dengan menyiapkan media kotak dan benda konkretnya
- 2. Dimulai dari menjelaskan konkret 1x1 sampai 10x10. Berikut ini adalah contoh cara menjelaskan konkret untuk 4 x 4.
- a. Tunjukkan 4 kotak berisi 4 benda konkret (misalnya benda konkretnya adalah permen)
- b. Berikut contoh dialognya:
- Guru : G dan Siswa : S
- G : Anak-anak, coba lihat ibu guru memegang apa?
- S : Kotak, Bu
- G : Ada berapa kotak, dan apakah isi kotaknya?
- S : Ada 4 kotak masing-masing kotak berisi 4 permen
- G : 4 kotak berisi 4 permen simbolnya 4 ▢4 atau biasa kita kenal dengan 4 x 4.
Sekarang ibu guru mau bertanya, apakah arti 4x4?
- S : 4 ▢4 (dibaca empat kotak berisi 4 kelereng ).
- G : Nah, hasilnya adalah kita menghitung jumlah benda dalam semua kotak. Maka berapakah
hasil dari 4x4? Mari kita menghitung bersama..
- G + S : 4 dikotak pertama + 4 di kotak kedua + 4 di kotak ketiga + 4 di kotak keempat sama dengan 16.
- G : Betul… 4 x 4 sama dengan 16.
- c. Guru menuliskan seperti berikut ini:
KONKRET
- 1 ▢1 = 1 x 1
- 1 x 1 = 1 ▢1 = 1
Untuk selanjutnya guru menjelaskan konkret dari 2 x 2 sampai 10 x 10 seperti langkah pada poin 3b. Kemudian menuliskannya seperti berikut ini!
- 2 x 2 = 2 ▢2 = 2 + 2 = 4
- 3 x 3 = 3 ▢3 = 3 + 3 + 3 = 9
- 4 x 4 = 4 ▢4 = 4 + 4 + 4 + 4 = 16
- 5 x 5 = 5 ▢5 = 5 + 5 + 5 + 5 + 5 = 25
- 6 x 6 = 6 ▢6 = 6 + 6 + 6 + 6 + 6 + 6 = 36
- 7 x 7 = 7 ▢7 = 7 + 7 + 7 + 7 + 7 + 7 + 7 = 49
- 8 x 8 = 8 ▢8 = 8 + 8 + 8 + 8 + 8 + 8 + 8 + 8 = 64
- 9 x 9 = 9 ▢9 = 9 + 9 + 9 + 9 + 9 + 9 + 9 + 9 + 9 = 81
- 10 x 10 = 10 ▢10 = 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 = 100
Selanjutnya kita masuk tahap abstrak dengan menuliskan perkalian dan hasilnya seperti berikut ini:
ABSTRAK
- 1 x 1 = 1
- 2 x 2 = 4
- 3 x 3 = 9
- 4 x 4 = 16
- 5 x 5 = 25
- 6 x 6 = 36
- 7 x 7 = 49
- 8 x 8 = 64
- 9 x 9 = 81
- 10 x 10 = 100
MENCONGAK
Dalam gasing setelah konkret dan abstrak langkah selanjutnya adalah mencongak.
konkret → abstrak → mencongak
- Bagaimana mencongak kuadrat suatu bilangan?
Pertama kita fokus pada 3 x 3 dan 4 x 4
- 1 x 1 = 1 (perkalian 1)
- 2 x 2 = 4 (perkalian 2)
- 3 x 3 = 9
- 4 x 4 = 16
- 5 x 5 = 25 (perkalian 5)
- 6 x 6 = 36
- 7 x 7 = 49
- 8 x 8 = 64
- 9 x 9 = 81 (perkalian 9)
- 10 x 10 = 100 (perkalian 10)
- ini mudah diingat prosesnya
- 3 x 3 adalah 3 tambah 3 lalu tambah 3 lagi, hasilnya 9.
- 4 x 4 adalah 4 tambah 4 hasilnya 8 kemudian tambah 8 lagi, hasilnya 16
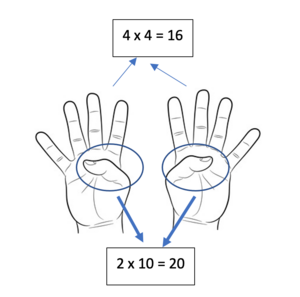
Sekarang kita fokus pada perkalian 6 x 6, 7 x 7 dan 8 x 8
- 1 x 1 = 1
- 2 x 2 = 4
- 3 x 3 = 9
- 4 x 4 = 16
- 5 x 5 = 25
- 6 x 6 = 36
- 7 x 7 = 49
- 8 x 8 = 64
- 9 x 9 = 81
- 10 x 10 = 100
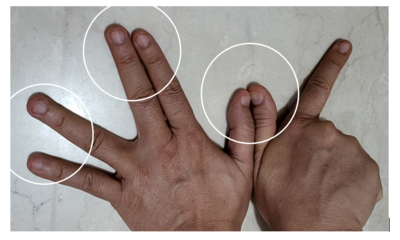
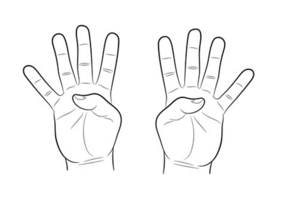
Untuk ini kita akan menggunakan jari dan pasangan 10.
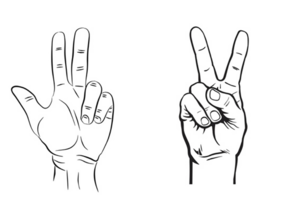
Menghitung 8 x 8
- Tangan kiri
- berapa pasangan sepuluh dari 8?
- 2
- Tunjukan 2 jari
Tangan kanan
- Berapa pasangan sepuluh dari 8?
- 2
- Tunjukan 2 jari
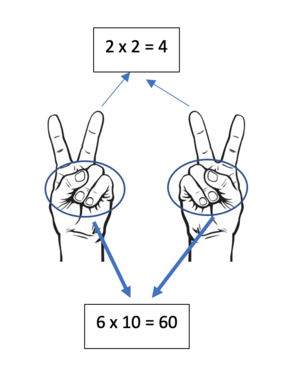
- Jari yang ditekuk bernilai 10.
- Karena ada 6 jari yang ditekuk maka nilainya 6 x 10 = 60
- Jari yang berdiri dikalikan
- yaitu 2 x 2 = 4
- Jumlahkan 60 dan 4. Itulah hasil perkalian 8 x 8
- Jadi 8 x 8 = 64
Menghitung 7 x 7
- Tangan kiri
- berapa pasangan sepuluh dari 7?
- 3
- Tunjukan 3 jari
Tangan kanan
- Berapa pasangan sepuluh dari 7?
- 3
- Tunjukan 3 jari
- Jari yang ditekuk bernilai 10.
- Karena ada 4 jari yang ditekuk maka nilainya 4 x 10 = 40
- Jari yang berdiri dikalikan
- yaitu 3 x 3 = 9
- Jumlahkan 40 dan 9. Itulah hasil perkalian 7 x 7
- Jadi 7 x 7 = 49
Menghitung 6 x 6
- Tangan kiri
- berapa pasangan sepuluh dari 6?
- 4
- Tunjukan 4 jari
Tangan kanan
- Berapa pasangan sepuluh dari 6?
- 4
- Tunjukan 4 jari
- Jari yang ditekuk bernilai 10.
- Karena ada 2 jari yang ditekuk maka nilainya 2 x 10 = 20
- Jari yang berdiri dikalikan
- yaitu 4 x 4 = 16
- Jumlahkan 20 dan 16. Itulah hasil perkalian 6 x 6
- Jadi 6 x 6 = 36
Alasan perkalian jari
- Misal kita hendak menghitung 8 x 7
- 8 x 7 = (10-2)(10-3) = 100 – 20 – 30 + 2x3
- Pertama kita tekuk 10 jari. Tiap jari yang ditekuk adalah bernilai 10. Nilainya 100
- Pasangan 8 adalah 2. Tangan kiri kita naik 2 jari.
- Jari yang ditekuk tinggal 8 nilainya 80
- Pasangan 7 adalah 3. Tangan kanan kita naik 3 jari.
- Jari yang ditekuk tinggal 8 – 3 = 5. Nilainya 50
- Ini sama dengan 100 – 20 – 30 = 50.
- Kemudian jari yang berdiri dikalikan 2 x 3
- Hasilnya adalah 50 + 2 x3
- Ini sama 8 x 7 = (10-2)(10-3) = 100 – 20 – 30 + 2x3 = 50 + 2 x3 = 56
- Aktivitas 2a bermain dengan kuadrat
Tujuan: membantu anak mencongak 6 x 6, 7 x 7 dan 8 x 8.
- Jumlah siswa 7 orang
- Buat lingkaran, satu siswa ditengah.
- Siswa ditengah membuat tulisan dikertas kecil 6 x 6, 7 x 7 dan 8 x 8 masing-masing 2 lembar.
- kertas dibagikan pada 6 siswa di lingkaran.
- Siswa yang mendapat tulisan itu berteriak menjawab hasil perkalian yang tertulis di kertas itu.
- Siswa yang lain mencek apakah jawaban itu benar atau tidak.
- Lakukan ini berulang-ulang.
Ini bisa divariasi Siswa menulis dikertas kecil salah satu perkalian 6 x 6 , 7 x 7 atau 8 x 8 , lalu minta siswa sebelahnya menjawabnya.
- Activitas 2b
Tujuan: melatih kemampuan mencongak siswa untuk kuadrat 1-10.
Siswa mencongak kuadrat 1-10 secara cepat.
- Activitas 2c
Tujuan: siswa mengerjakan secara cepat kuadrat 1-10
Ajak siswa berlatih dengan latihan berikut:
Latihan perkalian bilangan yang sama
Perkalian dengan 3 dan 4
Berdasarkan pengalaman, pada waktu kita mengajar perkalian 3 dan 4, kita akan melihat bahwa siswa mengalami kesulitan untuk mencongak perkalian 6 x 3, 7 x 3, 8 x 3, 6 x 4, 7 x 4 dan 8 x 4. Penggunaan lagu untuk mengingat perkalian ini sangat membantu siswa. Penggunaan lagu yang disertai gerakan akan membantu anak untuk mengoptimalkan otak kiri dan otak kanan serta meningkatkan kecerdasan kinestetik dan musik siswa.
Perkalian 3
- 1. Kita memulai dari tahap konkret yaitu dengan menyiapkan media kotak dan benda konkretnya
- 2. Dalam perkalian 3 atau perkalian dengan bilangan 3 masing-masing kotak berisi 3 benda konkret.
- 3. Dimulai dari menjelaskan konkret 1x3.Untuk perkalian 1x3 konsepnya sama seperti sebelumnya. Berikut adalah contoh cara menjelaskan konkret untuk 4x3
- a. Tunjukkan 4 kotak berisi 3 benda konkret (misalnya benda konkretnya adalah stik)
- b. Berikut contoh dialognya:
- Guru : G dan Siswa : S
- G : Anak-anak, coba lihat ibu guru memegang apa?
- S : Kotak, Bu
- G : Ada berapa kotak, dan apakah isi kotaknya?
- S : Ada 4 kotak masing-masing kotak berisi 3 stik
- G : 4 kotak berisi 3 stik simbolnya 4 ▢3 atau biasa kita kenal dengan 4 x 3.
Sekarang ibu guru mau bertanya, apakah arti 4x3?
- S : 4 ▢3 (dibaca empat kotak berisi 3 stik ).
- G : Nah, hasilnya adalah kita menghitung jumlah benda dalam semua kotak. Maka berapakah
hasil dari 4x3? Mari kita menghitung bersama..
- G + S : 3 dikotak pertama + 3 di kotak kedua + 3 di kotak ketiga + 3 di kotak keempat sama dengan 12.
- G : Betul… 4 x 3 sama dengan 12.
- c. Guru menuliskan seperti berikut ini:
KONKRET
- 1 ▢3 = 1 x 3
- 1 x 3 = 1 ▢3 = 3
Untuk selanjutnya guru menjelaskan konkret dari 2 x 3 sampai 10 x 3 seperti langkah pada poin 3b. Kemudian menuliskannya seperti berikut ini (gunakan sistem coret jika diperlukan).
- 2 x 3 = 2 ▢3 = 3 + 3 = 6
- 3 x 3 = 3 ▢3 = 3 + 3 + 3 = 9
- 4 x 3 = 4 ▢3 = 3 + 3 + 3 + 3 = 12
- 5 x 3 = 5 ▢3 = 3 + 3 + 3 + 3 + 3 = 15
- 6 x 3 = 6 ▢3 = 3 + 3 + 3 + 3 + 3 + 3 = 18
- 7 x 3 = 7 ▢3 = 3 + 3 + 3 + 3 + 3 + 3 + 3 = 21
- 8 x 3 = 8 ▢3 = 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 = 24
- 9 x 3 = 9 ▢3 = 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 = 27
- 10 x 3 = 10 ▢3 = 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 = 30
Selanjutnya kita masuk tahap abstrak dengan menuliskan perkalian dan hasilnya seperti berikut ini:
ABSTRAK
- 1 x 3 = 3
- 2 x 3 = 6
- 3 x 3 = 9
- 4 x 3 = 12
- 5 x 3 = 15
- 6 x 3 = 18
- 7 x 3 = 21
- 8 x 3 = 24
- 9 x 3 = 27
- 10 x 3 = 30
MENCONGAK
Dalam gasing setelah konkret dan abstrak langkah selanjutnya adalah mencongak.
konkret → abstrak → mencongak
- Bagaimana mencongak perkalian 3?
- 1 x 3 = 3 (sudah di pelajari diperkalian 1)
- 2 x 3 = 6 (sudah di pelajari di perkalian 2)
- 3 x 3 = 9 (sudah dipelajari di perkalian bilangan yang sama)
- 4 x 3 = 12 👈
- 5 x 3 = 15 (Sudah dipelajari di perkalian 5)
- 6 x 3 = 18 👈
- 7 x 3 = 21 👈
- 8 x 3 = 24 👈
- 9 x 3 = 27 (Sudah dipelajari di perkalian 9)
- 10 x 3 = 30 (Sudah dipelajari di perkalian 10)
Untuk 4 x 3, kita bisa menghitung 3 + 3 = 6 kemudian hasilnya ditambahkan 6, jadi 4 x 3 = 12
- Ini mudah untuk dihafalkan siswa.
Untuk 6 x 3, 7 x 3, 8 x 3 kita gunakan lagu....
Lagu dengan gerakan membuat siswa lebih semangat belajar, memaksimalkan otak kiri dan otak kanan serta meningkatkan kemampuan kinestetik dan musik siswa.
Lagu perkalian 3 menggunakan nada sebagaimana pada video berikut. Perhatikan dalam video ini bagian ketika guru bertanya 6 x 3, 7 x 3 dan 8 x 3. Perhatikan gerakan-gerakannya dan nadanya.
Selesai nyanyi kita buat permainan berikut
- Guru mengatakan 6 x 3 lalu siswa menyebutkan 18 dengan irama lagu + gerakannya.
Atau
- Guru menyanyi 18, siswa menyebut 6 x 3
Lakukan ini berulang-ulang bergantian antara 6 x 3, 7 x 3 dan 8 x 3.
- Aktivitas 3a bermain perkalian 3
Tujuan: membantu anak mencongak 6 x 3, 7 x 3 dan 8 x 3.
- Kita ambil 6 potong kertas.
- Tiap kertas ditulis masing-masing bilangan 6, 7, 8 , 18. 21 dan 24.
- buat kelompok 4-6 siswa.
- Tiap siswa memegang kartu 6 kartu itu
- Guru mengeluarkan kartu 6 sambil menyebut 6 x 3
- Siswa mengeluarkan kartu 18 sambil melagukannya.
- Lakukan ini bergantian untuk 6, 7 dan 8
- Guru mengeluarkan kartu 18 sambil melagukannya...
- Siswa mengeluarkan kartu 6 sambil menyebut 6 x 3
- Lakukan ini bergantian untuk kartu 18, 21 dan 24.
Variasi lain
- Ambil 3 kertas ukuran A4.
- Tulis pada kertas itu bilangan 18, 21 dan 24.
- Siswa mengelilingi kertas ini.
- Guru menyebut 6 x 3
- Siswa rebutan menunjukan kertas bertuliskan 18.
- Siapa yang paling lambat diberi hukuman lompat (misalnya 3 kali)
- lakukan ini berulang-ulang sampai anak hafal perkalian 3.
- Activitas 3b
Tujuan: melatih kemampuan mencongak siswa untuk perkalian 3
Siswa mencongak perkalian 3 secara cepat.
- Activitas 3c
Tujuan: siswa mengerjakan secara cepat perkalian 3
Ajak siswa berlatih dengan latihan berikut:
Latihan perkalian 3
- Activitas 3d
Tujuan: siswa mengerjakan secara cepat perkalian 6 x 3, 7 x 3 dan 8 x 3
Ajak siswa berlatih dengan latihan berikut:
Latihan perkalian 3 (untuk 6, 7 dan 8)
Perkalian 4
- 1. Kita memulai dari tahap konkret yaitu dengan menyiapkan media kotak dan benda konkretnya
- 2. Dalam perkalian 4 atau perkalian dengan bilangan 4 masing-masing kotak berisi 4 benda konkret.
- 3. Dimulai dari menjelaskan konkret 1x4.Untuk perkalian 1x4 konsepnya sama seperti sebelumnya. Berikut adalah contoh cara menjelaskan konkret untuk 3x4
- a. Tunjukkan 3 kotak berisi 4 benda konkret (misalnya benda konkretnya adalah stik)
- b. Berikut contoh dialognya:
- Guru : G dan Siswa : S
- G : Anak-anak, coba lihat ibu guru memegang apa?
- S : Kotak, Bu
- G : Ada berapa kotak, dan apakah isi kotaknya?
- S : Ada 3 kotak masing-masing kotak berisi 4 stik
- G : 3 kotak berisi 4 stik simbolnya 3 ▢4 atau biasa kita kenal dengan 3 x 4.
Sekarang ibu guru mau bertanya, apakah arti 3x4?
- S : 3 ▢4 (dibaca tiga kotak berisi 4 stik ).
- G : Nah, hasilnya adalah kita menghitung jumlah benda dalam semua kotak. Maka berapakah
hasil dari 3x4? Mari kita menghitung bersama..
- G + S : 4 dikotak pertama + 4 di kotak kedua + 4 di kotak ketiga sama dengan 12.
- G : Betul… 3 x 4 sama dengan 12.
- c. Guru menuliskan seperti berikut ini:
KONKRET
- 1 ▢4 = 1 x 4
- 1 x 4 = 1 ▢4 = 4
Untuk selanjutnya guru menjelaskan konkret dari 2 x 4 sampai 10 x 4 seperti langkah pada poin 3b. Kemudian menuliskannya seperti berikut ini (gunakan sistem coret jika diperlukan).
- 2 x 4 = 2 ▢4 = 4 + 4 = 8
- 3 x 4 = 3 ▢4 = 4 + 4 + 4 = 12
- 4 x 4 = 4 ▢4 = 4 + 4 + 4 + 4 = 16
- 5 x 4 = 5 ▢4 = 4 + 4 + 4 + 4 + 4 = 20
- 6 x 4 = 6 ▢4 = 4 + 4 + 4 + 4 + 4 + 4 = 24
- 7 x 4 = 7 ▢4 = 4 + 4 + 4 + 4 + 4 + 4 + 4 = 28
- 8 x 4 = 8 ▢4 = 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 = 32
- 9 x 4 = 9 ▢4 = 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 = 36
- 10 x 4 = 10 ▢4 = 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 = 40
Selanjutnya kita masuk tahap abstrak dengan menuliskan perkalian dan hasilnya seperti berikut ini:
ABSTRAK
- 1 x 4 = 4
- 2 x 4 = 8
- 3 x 4 = 12
- 4 x 4 = 16
- 5 x 4 = 20
- 6 x 4 = 24
- 7 x 4 = 28
- 8 x 4 = 32
- 9 x 4 = 36
- 10 x 4 = 40
MENCONGAK
Dalam gasing setelah konkret dan abstrak langkah selanjutnya adalah mencongak.
konkret → abstrak → mencongak
- Bagaimana mencongak perkalian 4?
- 1 x 4 = 4 (sudah dipelajari di perkalian 1)
- 2 x 4 = 8 (sudah dipelajari di perkalian 2)
- 3 x 4 = 12 (sudah dipelajari di perkalian 3)
- 4 X 4 = 16 (sudah dipelajari di perkalian bilangan yang sama)
- 5 x 4 = 20 (sudah dipelajari di perkalian 5)
- 6 x 4 = 24 👈
- 7 x 4 = 28 👈
- 8 x 4 = 32 👈
- 9 x 4 = 36 (sudah dipelajari di perkalian 9)
- 10 x 4 = 40 (sudah dipelajari di perkalian 10)
Untuk mencongak perkalian 6 x 4, 7 x 4, 8 x 4 kita gunakan lagu....
Lagu dan gerakannya membuat siswa lebih semangat belajar, memaksimalkan otak kiri dan otak kanan serta meningkatkan kemampuan kinestetik dan musik siswa.
Irama lagu ini bisa dilihat dalam video berikut. Perhatikan bagian video dimana guru bertanya 6 x 4, 7 x 4 dan 8 x 4. Perhatikan gerakan-gerakannya.
Selesai nyanyi kita buat permainan berikut
- Guru mengatakan 6 x 4 lalu siswa menyebutkan 24 dengan irama lagunya.
Atau
- Guru menyanyi 24, siswa menyebut 6 x 4
Lakukan ini berulang-ulang bergantian antara 6 x 4, 7 x 4 dan 8 x 4.
- Aktivitas 3e bermain dengan perkalian 4
Tujuan: membantu anak mencongak 6 x 4, 7 x 4 dan 8 x 4.
- Kita ambil 6 potong kertas.
- Tiap kertas ditulis masing-masing bilangan 6, 7, 8 , 24. 28 dan 32.
- buat kelompok 4-6 siswa.
- Tiap siswa memegang 6 kartu itu
- Guru mengeluarkan kartu 6 sambil menyebut 6 x 4
- Siswa mengeluarkan kartu 24 sambil melagukannya.
- Lakukan ini bergantian untuk 6, 7 dan 8
- Guru mengeluarkan kartu 24 sambil melagukannya...
- Siswa mengeluarkan kartu 6 sambil menyebut 6 x 4
- Lakukan ini bergantian untuk kartu 24, 28 dan 32.
Variasi lain
- Ambil 3 kertas ukuran A4.
- Tulis pada kertas itu bilangan 24, 28 dan 32.
- Siswa mengelilingi kertas ini.
- Guru menyebut 6 x 4
- Siswa rebutan menunjukan kertas bertuliskan 24.
- Siapa yang paling lambat diberi hukuman lompat (misalnya 3 kali)
- lakukan ini berulang-ulang sampai anak hafal perkalian 4.
- Activitas 3f
Tujuan: melatih kemampuan mencongak siswa untuk perkalian 4
Siswa mencongak perkalian 4 secara cepat.
- Activitas 3g
Tujuan: siswa mengerjakan secara cepat perkalian 4
Ajak siswa berlatih dengan latihan berikut:
Latihan perkalian 4
- Activitas 3h
Tujuan: siswa mengerjakan secara cepat perkalian 6 x 4, 7 x 4 dan 8 x 4
Ajak siswa berlatih dengan latihan berikut:
Latihan perkalian 4 (untuk 6, 7 dan 8)
Perkalian 6,7 dan 8
Pada perkalian 6, 7 dan 8 yang tersisa untuk diingat adalah perkalian 6 x 7, 6 x 8 dan 7 x 8
Untuk konkret perkalian 8, 7 dan 6 sama seperti perkalian-perkalian sebelumnya. Berikut akan dijelaskan salah satu konkret dari perkalian 7 yaitu 6x7
- a. Tunjukkan 6 kotak masing-masing berisi 7 benda konkret (misalnya benda konkretnya adalah kelereng)
- b. Berikut contoh dialognya:
- Guru : G dan Siswa : S
- G : Anak-anak, coba lihat ibu guru memegang apa?
- S : Kotak, Bu
- G : Ada berapa kotak yang ibu miliki?
- S : Ada 6 kotak bu
- G : Berapa isi masing-masing kotak?
- S : ada 7 kelereng Bu...
- G : 6 kotak berisi 7 kelereng simbolnya 6 ▢7 atau biasa kita kenal dengan 6 x 7.
Sekarang ibu guru mau bertanya, apakah arti 6x7?
- S : 6 ▢7 (dibaca enam kotak berisi 7 kelereng ).
- G : Nah, hasilnya adalah kita menghitung jumlah benda dalam semua kotak. Maka berapakah
hasil dari 6x7? Mari kita menghitung bersama..
- G + S : 7 dikotak pertama + 7 di kotak kedua + 7 di kotak ketiga + 7 di kotak keempat + 7 di kotak kelima + 7 dikotak keenam sama dengan 42.
- G : Betul… 6 x 7 sama dengan 42.
- c. Guru menuliskan seperti berikut ini:
KONKRET Berikut adalah konkret dari perkalian 8, 7 dan 6. Guru kembali mengingatkan penjumlahan dengan menggunakan sistem coret.
- 1 x 8 = 1 ▢8 = 8
- 2 x 8 = 2 ▢8 = 8 + 8 = 16
- 3 x 8 = 3 ▢8 = 8 + 8 + 8 = 24
- 4 x 8 = 4 ▢8 = 8 + 8 + 8 + 8 = 32
- 5 x 8 = 5 ▢8 = 8 + 8 + 8 + 8 + 8 = 40
- 6 x 8 = 6 ▢8 = 8 + 8 + 8 + 8 + 8 + 8 = 48
- 7 x 8 = 7 ▢8 = 8 + 8 + 8 + 8 + 8 + 8 + 8 = 56
- 8 x 8 = 8 ▢8 = 8 + 8 + 8 + 8 + 8 + 8 + 8 + 8 = 64
- 9 x 8 = 9 ▢8 = 8 + 8 + 8 + 8 + 8 + 8 + 8 + 8 + 8 = 72
- 10 x 8 = 10 ▢8 = 8 + 8 + 8 + 8 + 8 + 8 + 8 + 8 + 8 + 8 + 8 = 80
- 1 x 7 = 1 ▢7 = 7
- 2 x 7 = 2 ▢7 = 7 + 7 = 14
- 3 x 7 = 3 ▢7 = 7 + 7 + 7 = 21
- 4 x 7 = 4 ▢7 = 7 + 7 + 7 + 7 = 28
- 5 x 7 = 5 ▢7 = 7 + 7 + 7 + 7 + 7 = 35
- 6 x 7 = 6 ▢7 = 7 + 7 + 7 + 7 + 7 + 7 = 42
- 7 x 7 = 7 ▢7 = 7 + 7 + 7 + 7 + 7 + 7 + 7 = 49
- 8 x 7 = 8 ▢7 = 7 + 7 + 7 + 7 + 7 + 7 + 7 + 7 = 56
- 9 x 7 = 9 ▢7 = 7 + 7 + 7 + 7 + 7 + 7 + 7 + 7 + 7 = 63
- 10 x 7 = 10 ▢7 = 7 + 7 + 7 + 7 + 7 + 7 + 7 + 7 + 7 + 7 + 7 = 70
- 1 x 6 = 1 ▢6 = 6
- 2 x 6 = 2 ▢6 = 6 + 6 = 12
- 3 x 6 = 3 ▢6 = 6 + 6 + 6 = 18
- 4 x 6 = 4 ▢6 = 6 + 6 + 6 + 6 = 24
- 5 x 6 = 5 ▢6 = 6 + 6 + 6 + 6 + 6 = 30
- 6 x 6 = 6 ▢6 = 6 + 6 + 6 + 6 + 6 + 6 = 36
- 7 x 6 = 7 ▢6 = 6 + 6 + 6 + 6 + 6 + 6 + 6 = 42
- 8 x 6 = 8 ▢6 = 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 = 48
- 9 x 6 = 9 ▢6 = 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 = 54
- 10 x 6 = 10 ▢6 = 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 = 60
Selanjutnya kita masuk tahap abstrak dengan menuliskan perkalian dan hasilnya seperti berikut ini:
ABSTRAK
MENCONGAK
Pada perkalian 8, 7 dan 6 semakin sedikit perkalian yang dicongak. Untuk perkalian 8 perkalian yang dicongak secara berulang adalah 6x8 dan 7x8, pada perkalian 7 yang dicongak adalah 7x6 sedangkan pada perkalian 6 tidak ada lagi yang dicongak.
Selanjutnya kita akan mencongak 6 x 7, 6 x 8 dan 7 x 8. Caranya adalah dengan menggunakan pola. Polanya ada pada pemanfaatan jari dan pasangan 10.
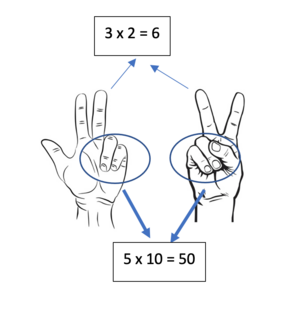
Menghitung 7 x 8 atau 8 x 7
- Tangan kiri
- berapa pasangan sepuluh dari 7?
- 3
- Tunjukan 3 jari
Tangan kanan
- Berapa pasangan sepuluh dari 8?
- 2
- Tunjukan 2 jari
- Jari yang ditekuk bernilai 10.
- Karena ada 5 jari yang ditekuk maka nilainya 5 x 10 = 50
- Jari yang berdiri dikalikan
- yaitu 3 x 2 = 6
- Jumlahkan 50 dan 6. Itulah hasil perkalian 7 x 8
- Jadi 7 x 8 = 56
Menghitung 6 x 8 atau 8 x 6
- Tangan kiri
- berapa pasangan sepuluh dari 6?
- 4
- Tunjukan 4 jari
Tangan kanan
- Berapa pasangan sepuluh dari 8?
- 2
- Tunjukan 2 jari
- Jari yang ditekuk bernilai 10.
- Karena ada 4 jari yang ditekuk maka nilainya 4 x 10 = 40
- Jari yang berdiri dikalikan
- yaitu 4 x 2 = 8
- Jumlahkan 40 dan 8. Itulah hasil perkalian 6 x 8
- Jadi 6 x 8 = 48
Menghitung 6 x 7
- Tangan kiri
- berapa pasangan sepuluh dari 6?
- 4
- Tunjukan 4 jari
Tangan kanan
- Berapa pasangan sepuluh dari 7?
- 3
- Tunjukan 3 jari
- Jari yang ditekuk bernilai 10.
- Karena ada 3 jari yang ditekuk maka nilainya 3 x 10 = 30
- Jari yang berdiri dikalikan
- yaitu 4 x 3 = 12
- Jumlahkan 30 dan 12. Itulah hasil perkalian 6 x 7
- Jadi 6 x 7 = 42
- Aktivitas 4a bermain dengan perkalian 6 x 7, 6 x 8 dan 7 x 8
Tujuan: membantu anak mencongak 6 x 7, 6 x 8 dan 7 x 8.
- Jumlah siswa 7 orang
- Buat lingkaran, satu siswa ditengah.
- Siswa ditengah membuat tulisan dikertas kecil 6 x 7, 6 x 8 dan 7 x 8 masing-masing 2 lembar.
- kertas dibagikan pada 6 siswa di lingkaran.
- Siswa yang mendapat tulisan itu berteriak menjawab hasil perkalian yang tertulis di kertas itu.
- Siswa yang lain mencek apakah jawaban itu benar atau tidak.
- Lakukan ini berulang-ulang.
Ini bisa divariasi Siswa menulis dikertas kecil salah satu perkalian 6 x 7 , 6 x 8 atau 7 x 8 , lalu minta siswa sebelahnya menjawabnya.
- Activitas 4b
Tujuan: melatih kemampuan mencongak siswa untuk perkalian 6,7 dan 8
Siswa mencongak perkalian 6, 7 dan 8
- Activitas 4c
Tujuan: siswa mengerjakan secara cepat perkalian 7x8, 6x8 dan 6x7
Tujuan: siswa mengerjakan secara cepat perkalian 7x8, 6x8 dan 6x7
Ajak siswa berlatih dengan latihan berikut:
Latihan perkalian 7x8, 6x8 dan 6x7
- Activitas 4d
Tujuan: siswa mengerjakan secara cepat perkalian 8
Ajak siswa berlatih dengan latihan berikut:
Latihan perkalian 8
- Activitas 4e
Tujuan: siswa mengerjakan secara cepat perkalian 7.
Ajak siswa berlatih dengan latihan berikut:
Latihan perkalian 7
- Activitas 4f
Tujuan: siswa mengerjakan secara cepat perkalian 6.
Ajak siswa berlatih dengan latihan berikut:
Latihan perkalian 6
- Activitas 4g
Tujuan: siswa mengerjakan secara cepat perkalian 1 sampai 10
Ajak siswa berlatih dengan latihan berikut:
Latihan perkalian 1-10
Berikut ini video suit banyak jari untuk memperlancar belajar perkalian.
Berikut ini permainan menjawab perkalian bilangan 1 angka dengan bilangan 1 angka selama 1 menit tanpa henti
Perkalian Bilangan dua angka dengan bilangan satu angka
Kita sudah lewat titik kritis gasing. Artinya kita sudah siap untuk memanfaatkan perkalian bilangan satu angka untuk perkalian bilangan yang lebih besar. Disini kita akan mengalikan bilangan dua angka dengan bilangan satu angka.
Kita bagi perkalian ini menjadi dua bagian
- 1. Perkalian bilangan dua angka dan satu angka tetapi hasil perkalian satuannya < 10
- 2. Perkalian bilangan dua angka dan satu angka dengan perkalian satuannya ≥ 10
Perkalian bilangan dua angka dengan satu angka, hasil perkalian satuannya < 10
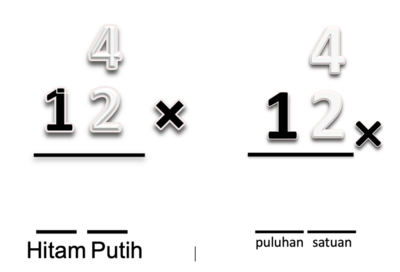
Dibagian ini kita akan menghitung perkalian bilangan dua angka dengan bilangan satu angka, tetapi hasil perkalian satuannya kurang dari 10. Pada bagian ini kita menggunakan kembali alat peraga kertas putih (kertas satuan) dan kertas hitam(kertas puluhan) yang selanjutnya disebut kartu puluhan dan kartu satuan.
Contoh 1: 4 x 12 = …
Untuk menjelaskannya kita menggunakan 3 tahapan gasing yaitu dari tahap konkret, abstrak kemudian mencongak.
KONKRET
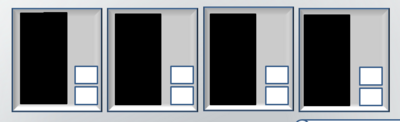
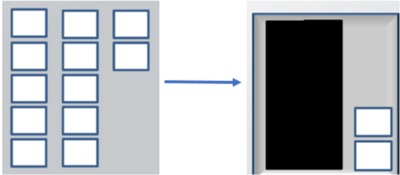
- 1.Guru menunjukkan media yang digunakan yaitu 4 kotak yang masing-masing berisi 12 (1 kartu hitam yang melambangkan 1 puluhan dan 2 kartu putih yang melambangkan 2 satuan) seperti pada gambar berikut:
- Contoh dialog:
- G : “Anak-anak, ada berapa kotak yang ada di depan ini? Dan berapakah isi masing-masing
kotaknya?”
- S : “Ada 4 kotak bu, masing-masing berisi 1 kartu hitam dan 2 kartu putih.”
- G : “1 kartu hitam dan 2 kartu putih, ini disebut berapa?”
- S : “1 kartu hitam melambangkan 1 puluhan, dan 2 kartu putih melambangkan 2 satuan sehingga nilainya 12 Bu ”
- G : “4 kotak masing-masing berisi 12 biasa kita kenal dengan 4 x 12.
Berapakah hasil dari 4 x 12? Mari kita hitung semua isi kotak.
- 2. Guru bersama siswa mengumpulkan masing-masing kartu hitam dan putih
- G : “Mari kita mulai menghitung dari kartu hitamnya. Dari 4 kotak masing-masing
terdapat 1 kartu hitam. Maka ada berapa kartu hitamnya?
- G+S : 1+1+1+1 sama dengan 4 kartu hitam (guru mengambil kartu hitam dari masing
masing kotak)
- G : “Selanjutnya kita menghitung kartu putihnya.”
- G+S : “2+2+2+2 sama dengan 8 kartu putih.”
- G : “Ada 4 kartu hitam dan 8 kartu putih, ini disebut berapa?”
- S : “48 bu, karena 4 kartu hitam itu melambangkan 4 puluhan dan 8 kartu putih itu melambangkan 8 satuan"
- G : “Jadi dapat disimpulkan bahwa 4 x 12 sama dengan 48.”
Guru dapat menulis :
- 4 x 12 = 4 ▢12 = 48
- ABSTRAK
- Disini kita akan menuliskan proses konkret dalam bentuk simbol-simbol (termasuk angka). Penjelasan abstrak ini dapat dilakukan bersamaan dengan penjelasan konkretnya.
Disini kartu hitam melambangkan puluhan dan kartu putih melambangkan satuan. Jumlah kotak dinyatakan dalam bentuk bilangan.
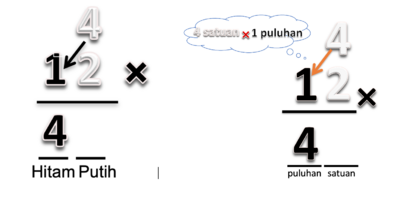
Kita tuliskan perkalian 4 x 12 dalam bentuk susun ke bawah.
- Pada proses konkret kita mengalikan 4 kotak dengan 1 kartu hitam. Proses ini dilukiskan secara abstrak sebagai perkalian antara bilangan 4 dengan 1 puluhan. Hasilnya adalah 4 puluhan.
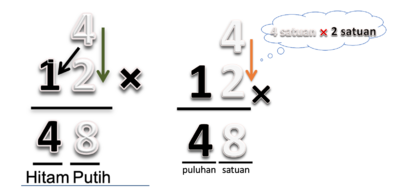
Proses berikutnya adalah mengalikan 4 kotak dengan 2 kotak putih. Proses ini dilukiskan secara abstrak sebagai perkalian antara bilangan 4 dengan 2 satuan. Hasilnya adalah 8 satuan.
Jadi, 4 x 12 = 48
Contoh 2: 12 x 4 =
KONKRET
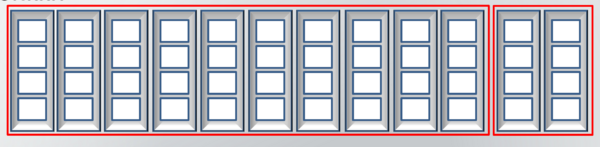
a. Guru menunjukkan media yang digunakan yaitu 12 kotak yang masing-masing berisi 4 kartu putih seperti pada gambar. Pisahkan 10 kotak pertama dari 2 kotak lainnya. Namakan 10 kotak sebagai kelompok 10 dan 2 kotak sebagai kelompok 2.
- Contoh dialog:
- G : “Anak-anak, ada berapa kotak yang ada di depan ini? Dan berapakah isi masing-masing
kotaknya?”
- S : “Ada 12 kotak bu, masing-masing berisi 4 kartu putih.”
- G : “12 kotak masing-masing berisi 4 benda biasa kita kenal dengan 12 x 4. Berapakah hasil dari 12x4? Mari kita hitung semua isi kotak.
b. Guru bersama siswa mengumpulkan isi masing-masing kotak yang dimulai dari 10 kotak (kelompok 10) selanjutnya menghitung 2 kotak berikutnya (kelompok 2).
- G : “Sekarang kita kumpulkan 10 kotak (kelompok 10) yang masing-masing berisi 4 kartu putih.
Jadi ada berapa kartu putihnya?”
- S : “40 kartu putih bu.”
- G: “Kita ubah 10 kartu putih menjadi 1 kartu hitam. Sehingga kita punya berapa kartu
hitamnya?”
- S : “4 kartu hitam bu?”
- G :”Berikutnya kita kumpulkan 2 kotak sisanya (kelompok 2) yang masing-masing berisi 4 kartu
putih. Jadi ada berapa kartu putihnya?”
- S : “8 kartu putih, bu”
- G : “Sehingga terdapat 4 kartu hitam dan 8 kartu putih yang disebut 48, karena 4 kartu hitam melambangkan 4 puluhan dan 8 kartu putih melambangkan 8 satuan.
Jadi 12x4=48
- ABSTRAK
Proses konkret diatas dapat dipermudah jika dituliskan dalam bentuk simbol-simbol yang kita sebut proses Abstrak. Penjelasan abstrak ini dapat dilakukan bersamaan dengan penjelasan konkretnya.
Disini jumlah kotak dinyatakan dalam bentuk bilangan
4 kartu putih dinyatakan sebagai 4 satuan.
Prosesnya adalah sebagai berikut
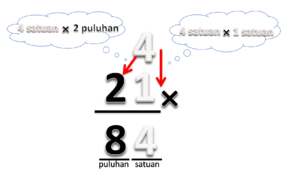
- Pertama kita tuliskan perkalian 12 x 4 ini dalam bentuk susun ke bawah. Kita buat 2 kolom. Kolom pertama hasilnya kita tulis sebagai hitam dan putih (yang melambangkan banyaknya kartu hitam dan kartu putih), sedangkan kolom kedua hasilnya kita tulis sebagai puluhan dan satuan.
- Proses selanjutnya adalah mengalikan 10 kotak (kelompok 10) dengan 4 kartu putih. Secara abstrak proses ini dilukiskan dengan mengalikan bilangan 10 dengan 4 satuan. Hasilnya adalah 40 satuan atau 4 puluhan
Kemudian kita mengalikan 2 kotak dengan 4 kartu putih ini. Secara abstrak ini dilukiskan dengan mengalikan bilangan 2 dengan 4 satuan. Hasilnya adalah 8 satuan.
Hasilnya adalah 4 puluhan dan 8 satuan yang mempunyai nilai 48.
Jadi 12 x 4 = 48
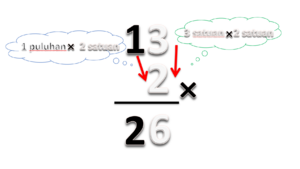
Perhatikan contoh berikut ini 4 x 21 = 84 dan 13 x 2 = 26
Berikut ini video menjelaskan perkalian 2 x 24 =
MENCONGAK
Dari langkah abstrak di atas, maka kita akan dapat menghitung cepat (mencongak) dari depan. Misalnya: 12 x 3 = ….
- a. 1x3 = 3 (puluhan x satuan)
- b. 2x3 = 6 (satuan x satuan)
- c. Dapat disimpulkan 12 x 3 = 36
- Aktivitas 5a
Tujuan: melatih kemampuan mencongak siswa untuk perkalian dua angka dengan satu angka, dengan perkalian satuannya kurang dari 10.
Soal yang diberikan seperti soal berikut:
- Error creating thumbnail: Unable to save thumbnail to destination
Siswa mencongak perkalian secara cepat.
Aktivitas 5b
Tujuan: siswa mengerjakan secara cepat perkalian dua angka dengan satu angka, dengan perkalian satuannya kurang dari 10.
Ajak siswa berlatih dengan latihan berikut:
Latihan perkalian dua angka dengan satu angka level 1
Perkalian bilangan dua angka dengan satu angka, hasil perkalian satuannya ≥ 10
Di bagian ini kita akan menghitung perkalian bilangan dua angka dengan bilangan satu angka (atau perkalian bilangan satu angka dengan bilangan dua angka), dengan hasil perkalian satuannya ≥ 10 (dibaca lebih besar atau sama dengan 10)
Sama seperti pada pembahasan sebelumnya bahwa untuk menjelaskan materi ini kita akan melalui tiga tahap, yaitu konkret, abstrak dan mencongak.
Misalnya untuk menjelaskan 4x13, penjelasannya adalah sebagai berikut:
KONKRET
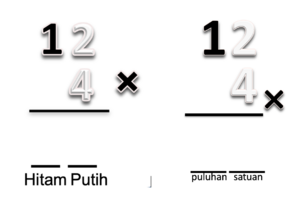
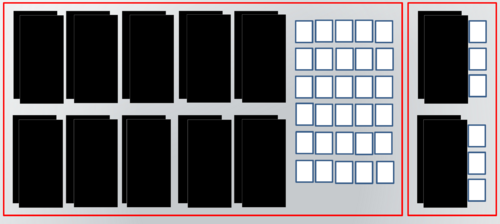
1. Guru menunjukkan media yang digunakan yaitu 4 kotak yang masing-masing berisi 13 kartu (1 kartu hitam dan 3 kartu putih) seperti pada gambar berikut:
Contoh dialog:
- G : “Anak-anak, ada berapa kotak yang ada di depan ini? Dan berapakah isi masing-masing
kotaknya?”
- S : “Ada 4 kotak bu, masing-masing berisi 1 kartu hitam dan 3 kartu putih.”
- G : “1 kartu hitam dan 3 kartu putih, ini disebut berapa?”
- S : “13 Bu, karena 1 kartu hitam melambangkan 1 puluhan dan 3 kartu putih melambangkan 3 satuan.”
- G : “4 kotak masing-masing berisi 13 biasa kita kenal dengan 4 x 13. Berapakah hasil dari
4 x 13? Mari kita hitung semua isi kotak.
- 2. Guru bersama siswa mengumpulkan masing-masing kartu hitam dan putih
- G : “Mari kita mulai menghitung dari kartu hitamnya. Dari 4 kotak masing-masing
terdapat 1 kartu hitam. Maka ada berapa kartu hitamnya?
- G+S : 1+1+1+1 sama dengan 4 kartu hitam (guru mengambil kartu hitam dari masing
masing kotak)
- G : “Selanjutnya kita menghitung kartu putihnya.”
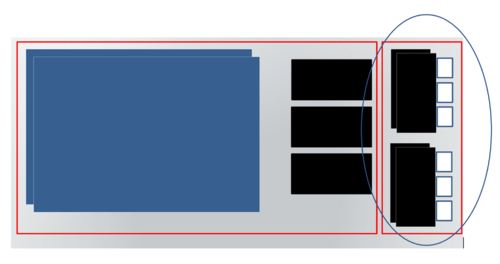
- G+S : “3+3+3+3 sama dengan 12 kartu putih. Nah, dari 12 kartu putih ini, bisa kita tukar dengan 1 kartu hitam dan 2 kartu putih.
G : “Selanjutnya kita gabungkan 1 kartu hitam ini dengan 4 kartu hitam yang ada sebelumnya. Sehingga menjadi 5 kartu hitam. Sekarang terdapat berapa kartu hitam dan putihnya?”
S : “Ada 5 kartu hitam dan 2 kartu putih, ini disebut 52 karena kartu hitam melambangkan puluhan dan kartu putih melambangkan satuan.”
G : “Jadi dapat disimpulkan bahwa 4 x 13 sama dengan 52. Yang terdiri dari 5 puluhan dan 2 satuan.”
ABSTRAK
Di bagian ini kita akan menuliskan proses konkret diatas dalam bentuk simbol-simbol termasuk angka-angka. Penjelasan abstrak ini dapat dilakukan bersamaan dengan penjelasan konkretnya.
Disini kartu hitam dilukiskan sebagai puluhan dan kartu putih sebagai satuan. Jumlah kotak dilukiskan dalam bentuk bilangan.
Kita tuliskan soalnya yaitu 4 x 13 dalam bentuk bersusun ke bawah. Nanti kalau sudah mahir siswa dapat mengerjakan secara mendatar
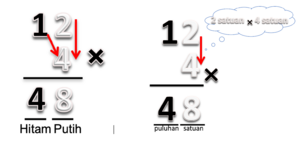
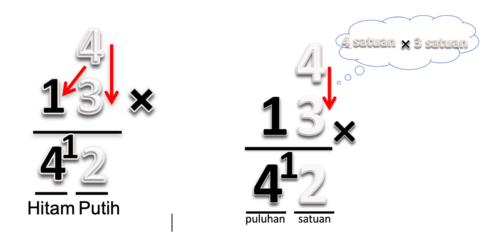
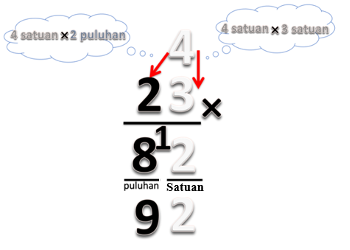
1. Langkah pertama adalah mengalikan 4 kotak dengan 1 kartu hitam. Ini dilambangkan sebagai mengalikan bilangan 4 dengan 1 puluhan. Hasilnya adalah 4 puluhan. Kita tuliskan 4 ditempat puluhan.
2. Berikutnya adalah mengalikan 4 kotak dengan 3 kartu putih. Ini dilambangkan sebagai mengalikan bilangan 4 dengan 3 satuan. Hasilnya adalah 12 satuan yang terdiri dari 1 puluhan dan 2 satuan. Angka 1 yang melambangkan puluhan ditulis lebih kecil, diletakan diantara puluhan satuan. Angka ini menunjukan 1 puluhan atau 10 satuan. Dapat ditulis seperti pada gambar.
3. Jumlahkan 4 puluhan dan 1 puluhan yang ditulis kecil. Sehingga menjadi 5 puluhan dan 2 satuan, seperti pada gambar.
Jadi, hasil dari 4 x 13 adalah 52 yang terdiri dari 5 puluhan dan 2 satuan.
Berikut ini contoh lain dari perkalian 2 angka dengan 1 angka
- Untuk menghitung 4 x 23
- Kalikan puluhannya 4 x 2 = 8.
- Kalikan satuannya 4 x 3 = 12
- Tulis hasilnya 4 x 23 = 812
- Jumlahkan puluhannya 8 + 1 = 9
- Jadi hasilnya 4 x 23 = 812 = 92
Video berikut ini menunjukan lebih detil bagaimana melakukan perkalian 2 angka dengan 1 angka
Kalau sudah mengerti konsep perkalian 2 angka dengan 1 angka, kita bisa melakukan perkalian ini secara mencongak seperti ditunjukan pada video berikut ini.
Berikut ini video micro teaching pelatihan GASING, seorang peserta menjelaskan perkalian 4 x 67 =
Setelah latihan soal yang disajikan secara bersusun selanjutnya disajikan secara mendatar.
Lakukan ini secara berulang-ulang. Dengan latihan terus-menerus siswa akan semakin mahir menghitung hasil perkalian 2 angka dengan 1 angka.
MENCONGAK
Pada tahap mencongak siswa akan diarahkan menyebutkan hasil perkalian hanya dengan melihat soal tanpa menulis bentuk abstrak dari hasil perkalian itu. Pada tahap ini siswa diarahkan untuk membayangkan angka. Hal ini melatih kecerdasan visual anak.
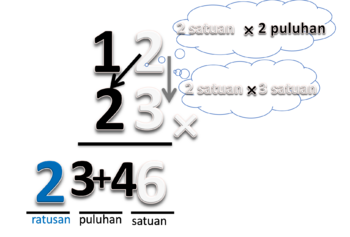
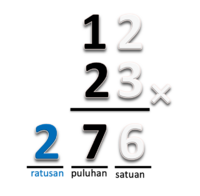
Bagaimana cara menentukan hasil perkalian 24 x 7 dengan cara mencongak? Perhatikan langkah berikut:
1. Kalikan 2 x 7. Hasilnya adalah 14. (ingat banyaknya puluhan adalah 14)
2. Kalikan 4x7. Hasilnya adalah 28 yang terdiri dari 2 puluhan dan 8 satuan.
3. Ingat kembali bahwa terdapat 14 puluhan sebelumnya maka gabungkan dengan 2 puluhan menjadi 16 puluhan dan masih ada 8 satuan. (cara mengingat : 1428 , gabungkan 14 dan 2 menjadi 16 sehingga menjadi 168)
4. Jadi 24 x 7 adalah 168.
5. Lakukan ini secara berulang-ulang dengan soal yang berbeda. Semakin sering siswa berlatih mencongak maka semakin bagus kecerdasan visualnya.
- Aktivitas 5c
Tujuan: melatih kemampuan mencongak siswa untuk perkalian dua angka dengan satu angka, dengan perkalian satuannya ≥ 10
Soal yang diberikan seperti soal berikut:
Siswa mencongak dengan cepat perkalian bilangan dua angka dengan bilangan satu angka.
Aktivitas 5d
Tujuan: siswa mengerjakan secara cepat perkalian dua angka dengan satu angka, dengan perkalian satuannya ≥ 10 level 2
Ajak siswa berlatih dengan latihan berikut:
Latihan perkalian dua angka dengan satu angka level 2
Aktivitas 5e
Tujuan: siswa mengerjakan secara cepat perkalian dua angka dengan satu angka, dengan perkalian satuannya ≥ 10 level 3
Ajak siswa berlatih dengan latihan berikut:
Latihan perkalian dua angka dengan satu angka level 3
Perkalian bilangan dua angka dengan bilangan dua angka
Perkalian dua angka dengan dua angka kita bagi dalam dua bagian
1. Perkalian bilangan dua angka dengan dua angka untuk angka kecil. Disini hasil jumlah perkalian angka puluhan dengan angka satuan atau perkalian angka satuannya kurang dari 10.
2. Perkalian bilangan dua angka dengan dua angka untuk angka besar. Disini hasil perkalian angka puluhan dengan angka satuan atau perkalian angka satuannya lebih besar atau sama dengan 10.
Perkalian Bilangan dua angka dengan bilangan dua angka untuk angka kecil
Dibagian ini kita akan bahas perkalian bilangan dua angka dengan bilangan dua angka untuk angka kecil.
Maksudnya jumlah perkalian angka puluhan dengan angka satuan atau perkalian angka satuannya kurang dari 10.
Contoh 12 x 23 =
Pada perkalian 2 angka dengan 2 angka
KONKRET
- Menurut arti perkalian, 12 x 23 = adalah kita menghitung berapa jumlah benda dalam 12 kotak yang berisi masing-masing 23 benda.
- 12 x 23 = 12 ▢23
- Ini ada 12 kotak
- Tiap kotak terdiri dari 23 kartu putih yang diwakili oleh 2 kartu hitam dan 3 kartu putih.
- 12 kotak ini kita kelompokkan dalam kelompok 10 dan kelompok 2.
Proses perhitungannya dimulai dari perhitungan isi kelompok 10 yang dimulai dari perhitungan kartu hitam. Pada kelompok 10 tiap kotaknya terdiri dari 2 kartu hitam maka kita hitung 2+2+2+2+2+2+2+2+2+2=20 kartu hitam.
Selanjutnya kita menghitung kartu putih yang terdapat pada kelompok 10 yaitu 3+3+3+3+3+3+3+3+3+3 = 30 kartu putih
- Jadi kita punya 20 kartu hitam dan 30 kartu putih
- 10 kartu hitam nilainya sama nilainya dengan 1 kartu biru, sehingga 20 kartu hitam dapat ditukar menjadi 2 kartu biru (Kartu biru ini akan kita sebut kartu ratusan karena berisi 100 kartu satuan).
- Selanjutnya 30 kartu putih pada kotak kelompok 10 ditukar menjadi 3 kartu hitam karena 10 kartu putih dapat ditukar menjadi 1 kartu hitam.
- Sekarang, kita menghitung kartu pada kotak kelompok 2. Pada kelompok 2, jumlah kartu hitam adalah 2 + 2 = 4 buah dan jumlah kartu putih adalah 3+3 = 6.
Kartu hitamnya kita jumlahkan 3 + 4 = 7.
Jadi kita punya 2 kartu biru, 7 kartu hitam dan 6 kartu putih.
Nilainya adalah 276 karena 2 kartu biru melambangkan 2 ratusan, 7 kartu hitam melambangkan 7 puluhan dan 6 kartu putih melambangkan 6 satuan.
Jadi 12 x 23 = 276
ABSTRAK
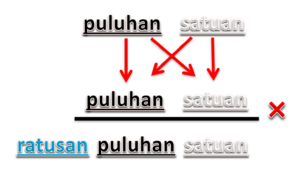
Berdasarkan tahap konkret yang telah dilakukan sebelumnya, terdapat 3 langkah untuk menyelesaikan perkalian 2 angka dengan 2 angka.
1. Puluhan x puluhan 2. (puluhan x satuan) + (satuan x puluhan) 3. Satuan x Satuan)
Perhatikan bagaimana ketiga Langkah itu kita peroleh (dalam Gasing kita harus mengerti kenapa suatu proses itu terjadi). Misalnya kita mau menghitung 12 x 23.
Disini kartu hitam dilambangkan dengan puluhan. Kartu putih dengan satuan. Dan jumlah kotak dalam bentuk bilangan.
1. Pada waktu kita mengalikan 10 kotak berisi 2 kartu hitam, kita seperti mengalikan bilangan 10 dengan 2 puluhan. Yaitu 10 x 2 puluhan = 20 puluhan atau sama dengan 2 ratusan.
2. Pada waktu kita mengalikan 10 kotak dengan 3 kartu putih, kita seperti mengalikan bilangan 10 dengan 3 satuan. Yaitu 10 x 3 satuan = 30 satuan atau sama dengan 3 puluhan
3. Demikian juga pada waktu kita mengalikan 2 kotak dengan 2 kartu hitam kita seperti mengalikan bilangan 2 dengan 2 puluhan. Yaitu 2 x 2 puluhan = 4 puluhan
4. Selanjutnya ketika kita mengalikan 2 kotak dengan 3 kartu putih kita seperti mengalikan bilangan 2 dengan 3 satuan yaitu 2 x 3 satuan = 6 satuan.
5. Kemudian puluhan kita jumlahkan 3 + 4 = 7 puluhan. Sehingga hasil akhirnya adalah 276 yant terdiri dari 2 ratusan, 7 puluhan dan 6 satuan.
Jadi disini prosesnya terlihat untuk mendapatkan 12 x 23 = 276.
Sekarang kita hitung 11 x 34
Disini kita siapkan 3 tempat untuk jawaban.
- Yang paling kiri adalah tempat untuk ratusan
- Yang tengah adalah tempat untuk puluhan
- Yang paling kanan adalah tempat untuk satuan
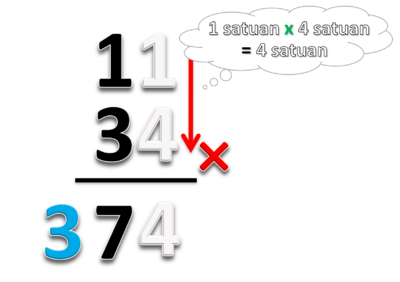
Cara menghitungnya
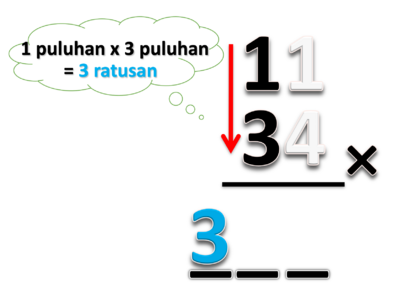
- 1. Kalikan puluhan dengan puluhan = 1 x 3 = 3.
- Hasilnya adalah 3 ratusan.
- Letakan 3 ditempat ratusan
- 2. Kalikan puluhan dengan satuan 1 x 4 = 4
- Kalikan satuan dengan puluhan 1 x 3 = 3
- Jumlahkan 3 + 4 = 7
- Hasilnya adalah 7 puluhan
- Letakan 7 ditempat puluhan
- 3. Kaikan satuan dengan satuan 1 x 4 = 4
- Hasilnya adalah 4 satuan
- Letakan 4 ditempat satuan
Jadi hasilnya 11 x 34 = 374
Mudah kan....
MENCONGAK
Mencongak disini adalah membayangkan proses abstrak ini di otak (tanpa menulis).
Mencongak ini akan meningkatkan kecerdasan visual kita.
Latih sebanyak mungkin soal perkalian 2 digit ini secara mencongak, ini akan membantu otak kita semakin cepat menghitung.
Aktivitas 6a
Tujuan: siswa mengerjakan secara cepat perkalian dua angka dengan dua angka untuk bilangan yang angkanya kecil Ajak siswa berlatih dengan latihan berikut:
Latihan perkalian bilangan dua angka dengan bilangan satu angka
Perkalian bilangan dua angka dengan bilangan dua angka untuk angka besar
Konsep perkalian bilangan 2 angka dengan 2 angka untuk angka besar sama dengan konsep perkalian untuk angka kecil yaitu
- puluhan x puluhan
- Puluhan x satuan + satuan x puluhan
- satuan x satuan
Contoh: 14 x 23
Kita siapkan 3 tempat
- Yang paling kiri untuk nilai tempat ratusan
- Yang tengah untuk nilai tempat puluhan
- Yang paling kanan untuk nilai tempat satuan
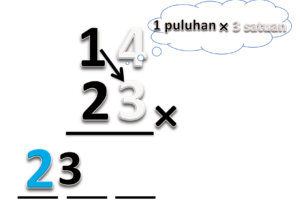
- Kalikan puluhan dengan puluhan
- Hasilnya 1 x 2 = 2
- Tempatkan 2 ditempat ratusan
- Kalikan puluhan dengan satuan
- Hasilnya 1 x 3 = 3
- Tempatkan 3 ditempat puluhan
- Kalikan satuan dengan puluhan
- Hasilnya 4 x 2 = 8
- Tempatkan 8 ditempat puluhan
- Jumlahkan puluhannya 3 + 8 = 11
- Tempatkan 11 ditempat puluhan, angka 1 (ditulis agak kecil) menunjukan ratusan
- Jumlahkan ratusan 2 + 1 = 3
- Hasil sementara ratusan ada 3 dan puluhan ada 1
- Kalikan satuan dengan satuan 4 x 3 = 12
- Tempatkan 12 ditempat satuan, angka 1 (ditulis agak kecil) menunjukan puluhan
- jumlahkan puluhan 1 + 1 = 2
- Hasilnya adalah 3 ratusan, 2 puluhan dan 2 satuan
- 14 x 23 = 322
Video berikut ini menunjukan lebih detil bagaimana melakukan perkalian 2 angka dengan 2 angka
Kalau sudah mengerti konsep perkalian 2 angka dengan 2 angka, kita bisa melakukan perkalian ini secara mencongak seperti ditunjukan pada video berikut ini.
Aktivitas 6b
Tujuan: siswa mengerjakan secara cepat perkalian dua angka dengan dua angka level 2
Ajak siswa berlatih dengan latihan berikut:
Latihan perkalian dua angka dengan dua angka level 2
Aktivitas 6c
Tujuan: siswa mengerjakan secara cepat perkalian dua angka dengan dua angka level 3
Ajak siswa berlatih dengan latihan berikut:
Latihan perkalian dua angka dengan dua angka level 3
Perkalian bilangan yang mempunyai banyak angka nol atau bulat
Untuk perkalian bilangan dengan banyak nol (atau bulat) seperti 24.000 x 20 dapat dilakukan dengan mudah.
- Kalikan angka bukan nol (atau bulat) 24 x 2 = 48
- Tambahkan nol (atau bulat) dibelakang hasilnya 480.0000. Banyaknya nol (atau bulat) yang ditambahkan sama banyaknya nol (bulat) dari kedua bilangan yang dikalikan.
- jadi 24.000 x 20 = 480.000
Aktivitas 7
Tujuan: siswa mengerjakan secara cepat perkalian bilangan yang mempunyai nol (bulat) dibelakangnya.
Ajak siswa berlatih dengan latihan berikut:
Latihan perkalian dengan bilangan yang mempunyai nol (bulat) dibelakangnya
Perkalian Bilangan tiga angka
Konsep perkalian bilangan 3 angka sama dengan konsep perkalian bilangan 2 angka. Perhatikan berbagai contoh yang diberikan.
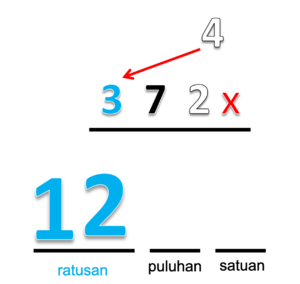
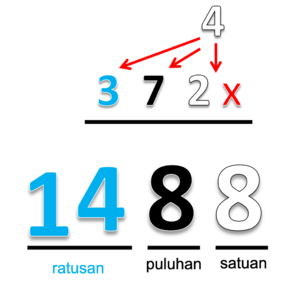
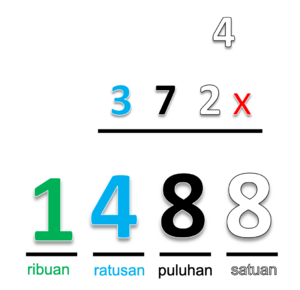
Contoh: 4 x 372 =
- Buat 3 tempat yang menunjukan nilai tempat ratusan, puluhan dan satuan.
- Kalikan 4 dengan ratusan
- Hasilnya 4 x 3 = 12
- Tulis 12 ditempat ratusan
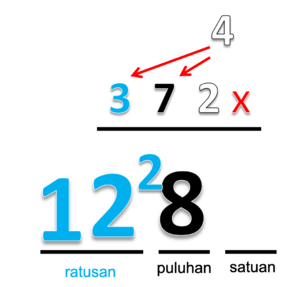
- Kalikan 4 dengan puluhan
- Hasilnya 4 x 7 = 28
- Tulis 28 ditempat puluhan
- Angka 2 dibuat agak kecil, menunjukan ratusan
- Kalikan 4 dengan satuan
- Hasilnya 4 x 2 = 8
- Tulis 8 ditempat satuan
- Jumlahkan ratusannya
- Hasilnya 12 + 2 = 14
- Ganti ratusannya, 12 menjadi 14
- 14 ratusan itu sama dengan 1 ribuan dan 4 ratusan
- Tempatkan 1 ditempat ribuan
- Jadi 4 x 372 = 1488
Contoh lain perkalian 3 angka dengan 1 angka dapat dilihat dalam video berikut.
Untuk perkalian 3 angka dengan 2 angka bersusun ke bawah dapat dilihat dalam video ini.
Untuk perkalian 3 angka dengan 2 angka bersusun ke samping dapat dilihat dalam video ini.
Untuk perkalian 3 angka dengan 3 angka bersusun ke bawah dapat dilihat dalam video ini.
Untuk perkalian 3 angka dengan 3 angka bersusun ke bawah untuk bilangan yang lebih besar dapat dilihat dalam video ini.
Untuk perkalian 3 angka dengan 3 angka bersusun ke samping dapat dilihat dalam video ini.
Untuk perkalian 4 angka dapat dilihat dalam video ini.
Ini cara alternatif perkalian bilangan 3 angka atau lebih.
Aktivitas 8a
Tujuan: siswa mampu mengerjakan perkalian tiga angka dengan satu angka
Ajak siswa berlatih dengan latihan berikut:
Latihan perkalian tiga angka dengan satu angka
Aktivitas 8b
Tujuan: siswa mampu mengerjakan perkalian tiga angka dengan dua angka
Ajak siswa berlatih dengan latihan berikut:
Latihan perkalian tiga angka dengan dua angka
Aktivitas 8c
Tujuan: siswa mampu mengerjakan perkalian tiga angka dengan tiga angka
Ajak siswa berlatih dengan latihan berikut:
Latihan perkalian tiga angka dengan tiga angka
Catatan: Untuk video dilihatnya pakai QRIS