Difference between revisions of "范畴论下量子力学的范式转换"

From PKC
Jump to navigation Jump to search
 
(83 intermediate revisions by 3 users not shown)
Line 1: Line 1:
<big>=量子力学发展中体现的范式转换和范畴论观点=
<big>
 
[[File:Fig1.png|thumb|450px|History]]
[[File:Fig1.png|thumb|600px|History]]
=='''用偏序集描述量子力学中的范式转换'''==
本文从范畴论的角度梳理了量子力学发展的三个范式阶段：前范式时期，矩阵力学与波动力学对立时期，统一理论时期。细节的范式转换被表示在上面这幅图中，可以看出整个范式转换可以被偏序集刻画的。


==早期量子论==
==早期量子论==
===两朵乌云===
在量子力学建立二十余年之前，随着赫兹证明了电磁波的存在与玻尔兹曼建立统计物理学，整个物理学形成了一套自洽的体系。以经典力学，经典电磁理论与经典热力学，统计物理学三大学科作为支柱的物理学，已经能够解释现实世界中几乎一切现象。在这样的背景下，1900年，开尔文勋爵做了一篇著名的关于未来物理学展望的报告：《在热和光动力理论上空的19世纪乌云》<ref>Kelvin, Lord. Nineteenth century clouds over the dynamical theory of heat and light[J]. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science,1901,2(7). </ref>。在这篇报告中，开尔文勋爵提到了当时物理学界运用已有的知识无法解决的两大问题，并将其称为两朵乌云。这两朵乌云一是迈克尔逊-莫雷实验所测得的地球相对以太速度为零，二是黑体辐射理论与实验的不一致。这两个问题直接引发了二十世纪物理理论的革命。第一个问题导致了狭义相对论的诞生，而第二个问题导致了量子力学的建立。
在量子力学建立二十余年之前，随着赫兹证明了电磁波的存在与玻尔兹曼建立统计物理学，整个物理学形成了一套自洽的体系。以经典力学，经典电磁理论与经典热力学，统计物理学三大学科作为支柱的物理学，已经能够解释现实世界中几乎一切现象。在这样的背景下，1900年，开尔文勋爵做了一篇著名的关于未来物理学展望的报告：《在热和光动力理论上空的19世纪乌云》<ref>Kelvin, Lord. Nineteenth century clouds over the dynamical theory of heat and light[J]. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science,1901,2(7). </ref>。在这篇报告中，开尔文勋爵提到了当时物理学界运用已有的知识无法解决的两大问题，并将其称为两朵乌云。这两朵乌云一是迈克尔逊-莫雷实验所测得的地球相对以太速度为零，二是黑体辐射理论与实验的不一致。这两个问题直接引发了二十世纪物理理论的革命。第一个问题导致了狭义相对论的诞生，而第二个问题导致了量子力学的建立。
{{#ev:youtube|https://www.youtube.com/watch?v=i1TVZIBj7UA|||||start=0&end=259}}


===普朗克与黑体辐射===
下面这个页面展示了经典物理学面临的危机。从而引发科学革命的范式转换。
在物理学中，黑体这一概念被用来描述这样一种理想化的物体——能够吸收外来的全部电磁辐射，而不会有任何的反射与透射。在吸收了电磁辐射之后，黑体会以热辐射的形式将能量辐射出去，这种热辐射就被称为黑体辐射。在开尔文爵士发表报告之前，有两组科学家从两个不同的方向尝试对黑体辐射中，辐射能量与热辐射波长的关系进行了理论上的推导，但均与实验数据产生了系统性的偏差。1896年，维恩从经典热力学出发，假设气体分子辐射的频率只与其速度有关，得到了热辐射的维恩公式 。维恩公式所得到的辐射值在短波区与实验值的吻合度相当高，但是在长波区相交实验值偏低。1900年，为了修正长波段中维恩公式的系统偏离，瑞利从能量按自由度均分这一原理出发进行推导。1905年，金斯计算得到瑞利提出公式中的常数，最终得到了瑞利-金斯公式。这个公式在长波区与实验值相当吻合，但是在短波区存在着近乎荒谬的偏离，随着波长变短（紫外光区），辐射能量会趋于无穷。在发现这一问题后，金斯曾作过各种努力，企图解决这个问题。然而他发现，只要坚持经典的统计理论（能均分定律），瑞利公式中短波波段能量趋于无穷的荒谬结论就是不可避免的。经典物理的这一错误预言如此严重，历史上被人们称为“紫外灾难”。
 
基于已经完善的经典物理学所得到的结果无法解释物理现象，这是前所未有的。为了解决这个问题，显然需要提出新的理论。1901年，普朗克在其发表的论文中对维恩公式提出了修正。为了解决长波下维恩公式的偏离，普朗克将维恩推导过程中的一个积分步骤改为了累加。令人惊喜的是，更改后的公式与实验数据完全吻合。为了让这种数学上的处理方法有其物理解释，普朗克发现必须引入一个新的物理假设，能量在发射与吸收的过程中存在一个最小单位，所有能量必须以这个最小单位的整数倍进行转移。能量的这种性质就被称为量子化<ref>需要读者注意的是，在此前的许多关于量子物理史的文章中，都直接表示或暗示了以下这个观点，普朗克公式受到瑞利-金斯公式的启发，是将两个公式合为一体的结果。然而事实上，在普朗克提出其公式时，瑞利-金斯公式尚未建立。瑞利-金斯公式所导致的“紫外灾难”并不是普朗克建立黑体辐射定律的动机。“紫外灾难”的产生只是让更多物理学家承认经典物理学的局限性，从而正视普朗克公式的价值。</ref>。
 
在此之前，所有物理学家都认为，空间与时间（包括能量）应该是连续的。也就是说，在时间从第三秒走到第四秒间，必然会经过数轴上，三到四间的每一个数。然而为了解释黑体辐射问题，普朗克引入的假设表明，能量只有有限个状态而非无限连续。虽然从连续性到分立性的转化在数学上只是一个很小的转化，但这个假设却让物理学的根基产生了动摇。


===微粒还是波的争论：光电效应===
<big>'''[[Paradigm shift]]'''</big>
在普朗克提出他的假设之后不久，在另一个领域也发现了能量量子化的证据。关于光的本质是微粒还是波这一问题，历史上曾有许多科学家进行过激烈地辩论。在19世纪，杨氏双缝实验的结果与麦克斯韦方程组的建立表明了光是一种电磁波。然而几乎在麦克斯韦方程组建立的同时，光电效应也同时被发现了。1887年，赫兹在进行电磁波的相关实验时发现，当紫外线照射到金属电极上会产生电火花。进一步的实验表明，当光照射到金属上的时候，会激发金属表面的电子。这种关于光与电相互作用的现象就被称为“光电效应”。在光电效应的实验现象中，存在着与光的波动说相逆的证据。光的波动说认为，增加光的强度（即提高光束的能量）能够激发出更高能量的电子。但实验表明，增加光的强度只能激发出更多数量的电子。只有提高照射光线的频率，才能激发出更高能量的电子。


受到普朗克能量量子化思想的启发，爱因斯坦在1905年发表了《关于光的产生和转化的一个启发性观点》 以阐释光电效应的现象。在这篇论文中，爱因斯坦提出了光的量子化。“……从点光源发出的光线的能量不会在空间中连续分布，而是由位于空间中的有限数量的能量量子(energy quanta)组成，这些能量量子不能被分割，只能作为完整的单元产生或被吸收。”爱因斯坦在这篇论文中将量子化的光称为“光量子”(light quanta)，这一概念在之后被称为“光子”(photon)。从光子的角度出发，就可以轻松地解释光电效应的现象。由普朗克的理论可以推得，单个光子的能量仅与光的频率 有关：
'''新的问题'''
                                                      '''<math>E=h\cdot\nu</math>'''
式中h为普朗克常数。频率更高的光线中，单个光子要比频率低的光线含有更高的能量，因此当光子入射至金属表面时就能够激发出拥有更多动能的电子来。而强光包含了更多数量的光子，所以能够激发出更多数量的电子来。


基于光电效应，爱因斯坦提出的光量子论从更广的范围内验证了能量量子化的正确性，也为后续量子力学的研究铺平了一条道路。
除此之外，崭新的量子论面临着更大的问题。。1925年，为了解释谱线在在弱磁场下的一种复杂分裂——“反常塞曼效应”，科学家提出了电子自旋理论，然而这种理论要求引入一个1/2的量子数<ref>G. E. Uhlenbeck, S. Goudsmit. Ersetzung der Hypothese vom unmechanischen Zwang durch eine Forderung bezüglich des inneren Verhaltens jedes einzelnen Elektrons[J]. Naturwissenschaften,1925.</ref>，这是玻尔模型所没有给出预测的。同时，玻尔也发现了他的理论只能解决单电子的原子，如氢原子，一级电离的氦原子。然而，对多电子原子，玻尔模型无法给出任何有用的结论。
 
===玻尔的原子模型===
在讨论玻尔的原子模型前，我们首先要介绍在玻尔之前，科学家对物质微观结构的认识。1808年，道尔顿基于大量的化学实验总结出了他的原子理论，认为原子是最小的不可分割的实体，是所有化学元素的最基本组成单位。道尔顿的理论被认为是近代原子论的开端。1897年，J.J.汤姆孙在在研究阴极射线（也就是电子流）时，发现了首个亚原子单位——电子。由于当时缺乏其他的观测手段，虽然汤姆孙发现了原子内部的结构，但他只能通过猜测来想象内部结构的样式。汤姆孙基于猜测提出了历史上第一个原子结构，他认为电子像布丁中的葡萄干一样镶嵌在原子中。这一模型被后世称为“葡萄干布丁模型”。
 
1910年，卢瑟福（同时也是J.J.汤姆孙的学生）为了探究“布丁”的大小，用一束α射线轰击一张金箔，却发现了用布丁模型难以解释的现象，有少量α粒子产生了大角度的偏转 。基于这个实验现象，卢瑟福修正了汤姆孙的原子理论。在卢瑟福的新理论中，在原子的中央位置存在致密、带正电的原子核。带负电的电子围绕原子核，以特定的轨道运动。正是因为α粒子与原子核产生了碰撞，才会发生大角度散射 。这个模型又被称为“行星系统模型”。
 
行星系统模型虽然很好的解释了α粒子的散射，但是却存在一个致命的缺陷。基于经典电磁学，做圆周运动的电荷会向外辐射的能量。由于电子轨道半径小，运动速度快，所以电子辐射能量的速率极高。按经典理论计算，在相当短的时间内电子就应该失去能量从而坠入原子核中。
 
所幸，当时已有的另一项物理成就给玻尔提供了解决问题的灵感。早在中世纪，人们就发现任何元素在被加热时都会释放出含有特定波长的光线。但是元素发出光线的波长却一直没有一个恰当的理论进行描述。1885年，巴耳末通过大量的实验数据发现，对氢元素发出的一组光线，波长可以用这样的公式来描述：
                                      '''<math>\frac{1}{\lambda}=R(\frac{1}{2^2}-\frac{1}{n^2})</math> '''
其中n可以取3,4,5……。1888年，里德伯将这个公式进行了拓展，将氢可能发出的所有光线的波长都用一个公式进行概括：
                                      '''<math>\ \frac{1}{\lambda}=R(\frac{1}{n^2}-\frac{1}{m^2})</math>'''
其中n，m均为正整数。这一具有明显量子化特征的公式启发了玻尔，让他进行了大胆的假设。1913年，玻尔连发三篇论文，阐述了他的新模型与量子化的新证据。  玻尔的模型假设在原子核外，电子有固定的轨道，且每个轨道的电子角动量均为约化普朗克常数的整数倍，而元素所发出的光的能量，正来源于电子从高能量轨道回落至低能量轨道时所释放的能量。根据这样的假设，计算出的光的波长完美符合里德伯公式。
 
===更大的问题：经典还是量子===
作为卢瑟福行星模型的延续，玻尔模型引入了量子化条件，从而使整个体系具有鲜明的量子化特点。但是玻尔模型作为一个唯象理论，仍然无法解释为什么处在确定轨道上的电子就可以不向外辐射能量。在1925年，泡利提出了著名的泡利不相容原理后，电子在核外运动的图像就显得更加复杂。泡利不相容原理指出，两个电子不能处于相同的状态，即一个电子轨道上，只能同时容纳两个电子（正向与反向）。泡利不相容原理成功的解释了许多化学反应的基本原理，但这个理论同样也有唯象理论的通病：没有办法解释现象背后的根本原因。
 
除此之外，崭新的量子论面临着更大的问题。。1925年，为了解释谱线在在弱磁场下的一种复杂分裂——“反常塞曼效应”，科学家提出了电子自旋理论，然而这种理论要求引入一个1/2的量子数 ，这是玻尔模型所没有给出预测的。同时，玻尔也发现了他的理论只能解决单电子的原子，如氢原子，一级电离的氦原子。然而，对多电子原子，玻尔模型无法给出任何有用的结论。


玻尔是立足于经典物理理论建立原子模型的。在从经典到量子的转化过程中，玻尔理论不能解释为何在宏观条件下成立的经典理论，在围观的原子层面就必须加入量子化的条件。玻尔的理论终究只是经典理论向量子模型所做出的妥协。实验表明，旧量子论这一基于经典理论的修正无法解释所有的物理现象，物理学必须要有一个崭新的范式作为基石继续前进。
玻尔是立足于经典物理理论建立原子模型的。在从经典到量子的转化过程中，玻尔理论不能解释为何在宏观条件下成立的经典理论，在围观的原子层面就必须加入量子化的条件。玻尔的理论终究只是经典理论向量子模型所做出的妥协。实验表明，旧量子论这一基于经典理论的修正无法解释所有的物理现象，物理学必须要有一个崭新的范式作为基石继续前进。
Line 46: Line 20:
==量子体系的完善==
==量子体系的完善==
在第一部分中，我们讲述了量子力学出现的背景和早期量子论的种种尝试，但是诸如玻尔原子模型这样的理论是很难作为一个新的范式而指导下一个阶段的研究工作的，因为它还不够成熟，过多的应用了一些强制的“规定”，给电子赋予了过多的“特有性质”而失去了一般性。在这一部分中，我们将详细的研究科学家们是如何建立一个相对完善的体系的。
在第一部分中，我们讲述了量子力学出现的背景和早期量子论的种种尝试，但是诸如玻尔原子模型这样的理论是很难作为一个新的范式而指导下一个阶段的研究工作的，因为它还不够成熟，过多的应用了一些强制的“规定”，给电子赋予了过多的“特有性质”而失去了一般性。在这一部分中，我们将详细的研究科学家们是如何建立一个相对完善的体系的。
===物质波===
 
'''（1）矩阵力学的建立'''
 
德布罗意在了解玻尔原子模型之后企图通过引入一种周期性来解释角动量量子化。在1919-1921年，布里渊曾发表过一系列论文，阐述了电子在运动时激发周围的以太形成的一种波动。德布罗意没有从以太的角度出发而结合了相对论，将粒子从波的角度考虑，得到：
德布罗意在了解玻尔原子模型之后企图通过引入一种周期性来解释角动量量子化。在1919-1921年，布里渊曾发表过一系列论文，阐述了电子在运动时激发周围的以太形成的一种波动。德布罗意没有从以太的角度出发而结合了相对论，将粒子从波的角度考虑，得到：
                                   <math>\nu=\frac{mc^2}{h}\ \ \ \ \ \ \lambda=\frac{h}{p}</math>  
                                   <math>\nu=\frac{mc^2}{h}\ \ \ \ \ \ \lambda=\frac{h}{p}</math>  
Line 53: Line 29:
不难发现这个速度是有可能大于光速的，但是由于这个波不携带能量和信息，因此不违反相对论。德布罗意大胆的预言在1927年被戴维逊和革末所证实，他们在用电子束轰击金属镍时得到了与x射线衍射几乎一样的结果，从而证明了电子的波动性。
不难发现这个速度是有可能大于光速的，但是由于这个波不携带能量和信息，因此不违反相对论。德布罗意大胆的预言在1927年被戴维逊和革末所证实，他们在用电子束轰击金属镍时得到了与x射线衍射几乎一样的结果，从而证明了电子的波动性。


===矩阵力学的建立==
电子波动性的证实使得危机空前严重，也进一步推动了革命的进行。1920年海森堡开始研究反常塞曼效应并提出半整数量子数的解释，当时并未得到认可。1924-1925年间，他加入了克拉摩斯研究色散理论的团队，他发现原子理论中的轨道应当被一种更好的观点所代替<ref>大卫·C·卡西第.海森堡传[M].戈革译,商务印书馆,2002.</ref>，与此同时，他的研究方式开始脱离开物理模型而直接建立数学模型。
电子波动性的证实使得危机空前严重，也进一步推动了革命的进行。1920年海森堡开始研究反常塞曼效应并提出半整数量子数的解释，当时并未得到认可。1924-1925年间，他加入了克拉摩斯研究色散理论的团队，他发现原子理论中的轨道应当被一种更好的观点所代替 ，与此同时，他的研究方式开始脱离开物理模型而直接建立数学模型。


1925年海森堡开始研究氢原子光谱的问题，他受到BKS理论和玻尔对应理论的影响，确立了研究的出发点：“物理学应当从一些可以直接被实验观察和检验的物理量出发 ”，由此他放弃了轨道等经典概念来想象原子，只把光谱提供的具体数据作为工作对象，他提出了一种“表格”式的数学规则来表示原子吸收、发射辐射的过程。在把他的研究成果和玻恩交流后，玻恩才意识到这种“表格”就是已经被数学家所发明的矩阵。1925年9月，海森堡在《物理学报》上论文的发表，标志着矩阵力学的建立，同时由于他的理论物理意义不够清晰，因此并没能得到很多人的认可。在此之后，狄拉克发现用泊松括号[x,y]作用于经典哈密顿函数上，就得到了和海森堡矩阵形式完全一样的结论。3个月之后，海森堡用矩阵处理了自旋问题，很好的得到了半整数量子数的结果，并且将自旋作为电子的一种属性，避免了自旋经典解释中的种种问题。至此，一个新的研究范式已经初步建成。
1925年海森堡开始研究氢原子光谱的问题，他受到BKS理论和玻尔对应理论的影响，确立了研究的出发点：“物理学应当从一些可以直接被实验观察和检验的物理量出发 ”<ref>曹天元.上帝掷骰子吗?量子物理史话[M].辽宁:辽宁教育出版社,2011.5.</ref>，由此他放弃了轨道等经典概念来想象原子，只把光谱提供的具体数据作为工作对象，他提出了一种“表格”式的数学规则来表示原子吸收、发射辐射的过程。在把他的研究成果和玻恩交流后，玻恩才意识到这种“表格”就是已经被数学家所发明的矩阵。1925年9月，海森堡在《物理学报》上论文的发表，标志着矩阵力学的建立，同时由于他的理论物理意义不够清晰，因此并没能得到很多人的认可。在此之后，狄拉克发现用泊松括号[x,y]作用于经典哈密顿函数上，就得到了和海森堡矩阵形式完全一样的结论。3个月之后，海森堡用矩阵处理了自旋问题，很好的得到了半整数量子数的结果，并且将自旋作为电子的一种属性，避免了自旋经典解释中的种种问题。至此，一个新的研究范式已经初步建成。


===波动力学的建立===
'''（2）波动力学的建立'''
薛定谔于1922年开始在苏黎世大学任教，在1925年的大部分时间里，他仍在研究理想气体的量子统计问题，在与爱因斯坦的来往中得知了德布罗意的论文。他认为德布罗意在对量子规则的解释上与自己有相同之处。在德拜主持的一个讨论会上，薛定谔做了一个漂亮的报告，清晰地阐述了德布罗意如何给粒子配上一列波 ，德拜对于他只用几何图像来解释量子规则感到不满，德拜认为“讨论波的性质，必须要有一个波动方程”，从而促使薛定谔着手于研究波动方程。
 
薛定谔于1922年开始在苏黎世大学任教，在1925年的大部分时间里，他仍在研究理想气体的量子统计问题，在与爱因斯坦的来往中得知了德布罗意的论文。他认为德布罗意在对量子规则的解释上与自己有相同之处。在德拜主持的一个讨论会上，薛定谔做了一个漂亮的报告，清晰地阐述了德布罗意如何给粒子配上一列波<ref>赵凯华.创立量子力学的睿智才思——纪念矩阵力学和波动力学诞生80~81周年[J].大学物理,2006(09):1-9.</ref>，德拜对于他只用几何图像来解释量子规则感到不满，德拜认为“讨论波的性质，必须要有一个波动方程”，从而促使薛定谔着手于研究波动方程。


薛定谔最先着手于相对论性波动方程的研究，但结果与索末菲方程不一致因此失败。1926年初，他开始考虑非相对论性的波动方程，不到半年，就在Annalen der Physik杂志上发表了Quantisierung als Eigenw ertproblem第一、二、三、四部分论文，奠定了波动力学的基础。
薛定谔最先着手于相对论性波动方程的研究，但结果与索末菲方程不一致因此失败。1926年初，他开始考虑非相对论性的波动方程，不到半年，就在Annalen der Physik杂志上发表了Quantisierung als Eigenw ertproblem第一、二、三、四部分论文，奠定了波动力学的基础。
Line 67: Line 43:
在第一部分论文中，对于氢原子求解了本征值，得到了角向是球谐函数，径向与玻尔原子论符合的很好。在后续的几篇文章中，又成功地把波动理论推广到了含时微扰并解决了色散问题，得到了一般形式下的波动方程。
在第一部分论文中，对于氢原子求解了本征值，得到了角向是球谐函数，径向与玻尔原子论符合的很好。在后续的几篇文章中，又成功地把波动理论推广到了含时微扰并解决了色散问题，得到了一般形式下的波动方程。


===不确定性===
{{#ev:youtube|https://www.youtube.com/watch?v=TQKELOE9eY4|||||start=0&end=283}}
 
'''（3）不确定性'''
 
海森堡所使用的矩阵存在一个独特的性质，即矩阵的乘）法一般情况下是不可交换的即
海森堡所使用的矩阵存在一个独特的性质，即矩阵的乘）法一般情况下是不可交换的即
                         <math>p\times q\neq q\times p</math>
                         <math>p\times q\neq q\times p</math>
Line 75: Line 54:


==矩阵形式和波动形式的统一==
==矩阵形式和波动形式的统一==
===两种形式的争论===
'''两种形式的争论'''
在1926年薛定谔发表四部分文章的间隙中就已经证明了两种表述形式在数学上的一致性，同一时期，泡利，约尔当也各自证明了其等价性。但是两种竞争着的范式并没有因此而统一，争论还在进行。作为理论在数学上已经统一，但作为两种范式，在物理图像和对物理现象的解释上还存在巨大的分歧，也就是说还是不可通约的。回顾这两个范式在刚刚诞生时期的状况，矩阵力学直接以可观测的量为基础，强调数学导向而非经验式的构建物理图像，在解释自旋等问题上有很出色的表现，但是由于矩阵形式的晦涩和物理图像不清晰，没有得到大多数科学家的追随。波动力学从德布罗意理论出发，由于其数学形式接近于经典，因此得到了大多数科学家的追随，但是同样面临着物理意义不清晰的问题，在很长一段时间内都无法解释\psi的物理含义，只能含糊其词为一种尚没有观测到的分布。更严重的问题在于波恩在解释\psi的物理意义时引入了概率，坍缩等一系列与经典格格不入的概念，因而招致了爱因斯坦等科学家甚至是薛定谔本人的反对，这一部分将在后续进一步讨论。
 
===电子双缝实验===
在1926年薛定谔发表四部分文章的间隙中就已经证明了两种表述形式在数学上的一致性，同一时期，泡利，约尔当也各自证明了其等价性。但是两种竞争着的范式并没有因此而统一，争论还在进行。作为理论在数学上已经统一，但作为两种范式，在物理图像和对物理现象的解释上还存在巨大的分歧，也就是说还是不可通约的。回顾这两个范式在刚刚诞生时期的状况，矩阵力学直接以可观测的量为基础，强调数学导向而非经验式的构建物理图像，在解释自旋等问题上有很出色的表现，但是由于矩阵形式的晦涩和物理图像不清晰，没有得到大多数科学家的追随。波动力学从德布罗意理论出发，由于其数学形式接近于经典，因此得到了大多数科学家的追随，但是同样面临着物理意义不清晰的问题，在很长一段时间内都无法解释<math>\psi</math>的物理含义，只能含糊其词为一种尚没有观测到的分布。更严重的问题在于波恩在解释<math>\psi</math>的物理意义时引入了概率，坍缩等一系列与经典格格不入的概念，因而招致了爱因斯坦等科学家甚至是薛定谔本人的反对，这一部分将在后续进一步讨论。
这个实验本来是通过干涉探究电子的波动性的实验，但是在电子到底是粒子还是波的争论中，也就是两大范式的争论中，科学家们开始用仪器精确测定电子的运动轨迹来判断干涉过程的形成。出人意料地，当我们用仪器（例如云室）观测电子的运动轨迹或是探测电子从哪个缝穿过时，干涉条纹就会消失，呈现出粒子性而非波动性。
 
===统一===
<big>'''[[电子双缝实验]]'''</big>
海森堡从粒子性的角度推出了不确定性关系，但是玻尔却意识到不确定关系正是波和粒子之间的桥梁，1927年9月，他首次提出互补原理这一概念，从不确定性关系出发，量子现象无法用单一的经典的物理图像来描述，必须用互补原理加以解释。当波动性体现出来时，粒子性就会不那么明显，反之亦然。波和粒子在统一微观物体身上是互斥的，但在更高的层次是统一的。互补原理的提出几乎彻底的结束了波和粒子，矩阵和波动的长久的争论，探究微观粒子本身是电子还是波并没有物理意义，这取决于我们用何种方式去观测它。在电子双缝实验中，如果我们用仪器观测电子的轨迹，那么电子的波动性就会消失从而失去干涉条纹。波粒二象性的建立从物理图像上同意了矩阵和波动两个范式。两个貌似不可通约的范式被新的理论的发现而统一，共同构成了现代量子力学体系的基本范式。
 
==量子力学的发展==
==量子力学的发展==
===对量子现象的解释===
===对量子现象的解释===
随着矩阵力学和波动力学的统一、不确定性关系的提出和互补原理的提出，量子力学完善的范式已经基本建成，但新的危机立刻就产生了，即如何对复杂的理论加以物理图像上的清晰的解释。较为主流的一个学派是以不确定性和互补原理为主要理论，对量子现象加以概率解释的“哥本哈根”解释，这一解释的拥护者主要有玻尔、海森堡、泡利、约尔当等人。这一解释体系最大的反对者是保守地相信经典物理因果律关系的学派，以爱因斯坦为领导。值得一提，薛定谔虽然是波动力学的奠基人，但是他却不相信概率解释，而是因果律的坚定拥护者。
随着矩阵力学和波动力学的统一、不确定性关系的提出和互补原理的提出，量子力学完善的范式已经基本建成，但新的危机立刻就产生了，即如何对复杂的理论加以物理图像上的清晰的解释。较为主流的一个学派是以不确定性和互补原理为主要理论，对量子现象加以'''概率'''解释的“哥本哈根”解释，这一解释的拥护者主要有玻尔、海森堡、泡利、约尔当等人。这一解释体系最大的反对者是保守地相信经典物理因果律关系的学派，以爱因斯坦为领导。值得一提，薛定谔虽然是波动力学的奠基人，但是他却不相信概率解释，而是因果律的坚定拥护者。


由于哥本哈根解释是目前比较主流的一种解释，因此本文将以之为主体来讲述因果律派与哥本哈根派的争论过程，并在最后介绍几种其它的量子现象的解释。
由于哥本哈根解释是目前比较主流的一种解释，因此本文将以之为主体来讲述因果律派与哥本哈根派的争论过程，并在最后介绍几种其它的量子现象的解释。'''下面这个视频讲述了哥本哈根学派的诞生'''


===哥本哈根解释的基本内容===
{{#ev:youtube|https://www.youtube.com/watch?v=-HJhKuM-jX4|||||start=0&end=960}}
哥本哈根解释是以不确定性原理、互补原理和概率解释三者为主体所建立的。不确定性原理和互补原理表明，一个微观客体展现出什么样的性质是由我们以何种方式观测它所决定的，也就是说单独去谈论一个微观客体具有什么样的性质是没有意义的。这样的解释推翻了经典物理中的完全客观性。一个体系可以完全由波函数描述，在没有对一个量子体系观测的时候，量子体系按照薛定谔方程发展演化，这时候的体系是多个状态的叠加态，当我们对体系进行观测，波函数发生了坍缩，坍缩的过程具有随机性和不可逆性，也就是说体系从多个状态的叠加态变成了一个确定的状态。对于薛定谔方程中<math>\varphi</math>的意义，哥本哈根派不认为波函数有除了抽象的概念以外的任何真实存在，也就是说波函数不代表一个实体，当波函数按照一定的概率坍缩之后才能够代表一个实体。如果去探究在观测之前、坍缩之前的电子是什么状态、在哪个位置，哥本哈根解释中最不可思议的地方就展现出来：在观测（也就是波函数坍缩）之前，电子是没有意义的，不具有客观性和实在性，也就是说，真实存在的不是电子，而是“观测者观测电子”这一相互作用 。
 
'''（1）哥本哈根解释的基本内容'''
 
哥本哈根解释是以不确定性原理、互补原理和概率解释三者为主体所建立的。不确定性原理和互补原理表明，一个微观客体展现出什么样的性质是由我们以何种方式观测它所决定的，也就是说单独去谈论一个微观客体具有什么样的性质是没有意义的。这样的解释推翻了经典物理中的完全客观性。一个体系可以完全由波函数描述，在没有对一个量子体系观测的时候，量子体系按照薛定谔方程发展演化，这时候的体系是多个状态的叠加态，当我们对体系进行观测，波函数发生了坍缩，坍缩的过程具有随机性和不可逆性，也就是说体系从多个状态的叠加态变成了一个确定的状态。对于薛定谔方程中<math>\varphi</math>的意义，哥本哈根派不认为波函数有除了抽象的概念以外的任何真实存在，也就是说波函数不代表一个实体，当波函数按照一定的概率坍缩之后才能够代表一个实体。如果去探究在观测之前、坍缩之前的电子是什么状态、在哪个位置，哥本哈根解释中最不可思议的地方就展现出来：在观测（也就是波函数坍缩）之前，电子是没有意义的，不具有客观性和实在性，也就是说，真实存在的不是电子，而是“观测者观测电子”这一相互作用<ref>Everett·Hugh. Relative State Formulation of Quantum Mechanics[J]. Reviews of Modern Physics. 1957, 29: 454–462.</ref>。
 
'''（2）爱因斯坦的观点'''


===爱因斯坦的观点===
爱因斯坦反对哥本哈根解释的主要原因有以下两点：
爱因斯坦反对哥本哈根解释的主要原因有以下两点：


Line 98: Line 81:


===玻尔-爱因斯坦的伟大辩论===
===玻尔-爱因斯坦的伟大辩论===
这一阶段爱因斯坦和玻尔的争论是物理学史上最著名的辩论之一,从1927年第五届索尔维会议开始，两位科学家一直在进行关于量子体系完备性的争论。接下来这一部分将给出几个例子来构建争论的过程和量子力学体系的进一步完善。这些例子不仅体现了物理学家敏锐的洞察力和犀利的思维，也能够很好的诠释库恩的理论——范式具有不可通约性、在新的范式面前，很少有科学家能够由旧的范式“改宗”至新的范式
这一阶段爱因斯坦和玻尔的争论是物理学史上最著名的辩论之一,从1927年第五届索尔维会议开始，两位科学家一直在进行关于量子体系完备性的争论。接下来这一部分将给出几个例子来构建争论的过程和量子力学体系的进一步完善。这些例子不仅体现了物理学家敏锐的洞察力和犀利的思维，也能够很好的诠释库恩的理论——范式具有不可通约性、在新的范式面前，很少有科学家能够由旧的范式“改宗”至新的范式。
====光箱实验====
1930年第六届索尔维会议上，爱因斯坦提出了一个思想实验：假象有一个箱子，箱子中有若干光子，箱子上有一道可以控制的快门。控制快门打开很短的一段时间<math>\Delta t</math>，有一些光子通过快门去到箱子外面，这时用精确的秤测量光箱体系质量的减少为<math>\Delta m</math>，根据质能方程
                                  <math>\Delta E=\Delta mc^2</math>
可以精确计算出光箱体系的能量减少<math>\Delta E</math>，同时<math>\Delta t</math>又是可控的，因此时间和能量的不确定性都为零，海森堡的不确定性关系就不能得到保障 。
对此，玻尔给出了完美的解释：爱因斯坦忽略的问题在于如何精确测量光箱体系质量的减少。如果是在引力场中使用弹簧秤来测量，则在测量时光箱必定会有位移，光箱中的光子在引力场中的位移会产生广义相对论的引力红移现象，导致光子频率的改变（也就是周期的改变），这样就引起了能量和时间上的不确定性，经过计算，这恰好满足海森堡不确定性关系 。
====EPR佯谬====
1935年，爱因斯坦、波多尔斯基和罗森在Physics Review上发表了一篇题为《Can Quantum-Mechanical Description of Physics Reality Be Considered Complete？》的论文，质疑了量子力学体系的不完备性，由于这个论述已经被证伪，因此现在被称为EPR佯谬。


这篇论文基于定域实在性，首先给出了两个严格的定义，定义了完备性和物理实在要素 。然后给出了一个思想实验，假象一个静止的大粒子分裂成两个小粒子，向相反的方向运动，由于守恒律，它们的坐标，动量必定互为相反，因此对一个小粒子动量或位置的测量（由于定域性这并不会影响到另一个小粒子）就可以预测另一个小粒子的物理状态，因此小粒子的动量和位置都是物理实在要素。但是由于不确定性关系，二者不能同时准确测量，也就是说并不是每一个物理实在要素在量子体系中都有对应的部分，也就是量子体系是不完备的。爱因斯坦认为，量子体系的不完备性在于还有一些未被察觉到的变量，即隐变量在控制，而找到这些隐变量就可以消除量子力学中的随机性而恢复完全的因果性关系 。
下面，通过几个例子来展现物理学史上最伟大的思想碰撞


1951年，波姆提出了EPR佯谬的另一个版本（又称EPRB佯谬），即想象一个大的粒子，分裂成两个有自旋的小粒子，由于守恒律，二者的自旋必须相反，在观测之前，两个小粒子都处在自旋为↑和自旋为↓的叠加态，当这两个小粒子相距很远的时候，对其中一个粒子的自旋进行观测，发生了坍缩，而另一个粒子必然坍缩成为相反的自旋态，在这之间必定传递了某种信息，而由于二者坍缩发生在同一时间，因此这产生了一种超过光速的信息传递，违背了定域性原理 。
<big>'''[[Some interesting thought experiments]]'''</big>
 
对此，哥本哈根学派给出的解释是：在坍缩之前，两个小粒子是一个系统，一个整体，二者的自旋、位置等在坍缩前是无意义的，二者作为一个整体，坍缩成↑↓或↓↑某一个定态，在这之后，粒子才具有了实在性，才成为两个系统，因此这个过程中不存在信息的传递。
 
这也体现了库恩范式的不可通约性：在爱因斯坦看来，两个小粒子是两个体系，具有定域实在性，之间存在信息传递；而哥本哈根学派认为两个小粒子在观测之前没有实在性，是一个整体，不存在信息传递，由于不可通约性，想说服不同科学共同体的科学家是相当困难的事，因此直到爱因斯坦离世，海森堡等人都没能说服他。
 
====薛定谔的猫====
1935年，薛定谔在与爱因斯坦等人讨论ERP问题时逐渐产生了把原子尺度上的叠加态转移到宏观系统中的想法。最初他的设想是一种不稳定的火药处于爆炸与不爆炸的叠加态。最终，经过加工，他设计出一个思想实验：把一只猫关在一个封闭的容器中，并在容器中装有以下装置：一个盖革计数器中放有一个放射性物质原子，若衰变事件发生，则盖革计数器发出电信号，通过一系列装置打破装有氰化物的瓶子，猫被毒死，若没有发生衰变，则猫依然存活。由于单原子的衰变过程按照哥本哈根解释是由波函数描述的叠加态，因此在打开容器之前，猫也处于死亡/活着的叠加态 。
 
这一思想实验的巧妙之处在于将微观粒子的叠加态映射到宏观系统中，制造一种“荒谬感” ，但是出现这一“荒谬”的根本原因在于不同科学共同体之间对“观测”一词赋予了不同的涵义，哥本哈根学派认为外界对体系由干扰，有相互作用即为观测，因此，在盖革计数器对粒子是否衰变做出反应时，就认为粒子已经被观测了，因此容器中已经出现了坍缩，也自然不会出现死/活叠加的状态。
 
====其它解释====
根据20世纪末的一次调查，哥本哈根解释仍然是支持率最高的量子力学解释，并且由于退相干理论的发展，多世界解释（Many World Interpretation，简称MWI）逐渐获得了一部分人的支持 。这一解释假定有无数平行宇宙，每对一个量子态进行观测，就会分裂出多个平行宇宙，每个平行宇宙中都是一个可能的状态，而我们只处于某一个宇宙当中，且我们不可能得知其他宇宙中的状态 。


==贝尔不等式==
==贝尔不等式==
==='''定域性的范畴表述'''===
再次思考EPRB佯谬，虽然哥本哈根解释已经很好的处理了“信息超光速传递”这一问题，但是仍然无法否定隐变量假说，即无法找到那个控制着粒子坍缩的隐变量，也无法否定它的存在。英国物理学家约翰·贝尔的学生时期玻尔的量子论已经占据了物理学主流的地位，但贝尔更愿意相信波姆对EPR佯谬的化简以及他提出的隐变量假说，因此贝尔致力于设计一套实验，可以证明量子坍缩过程确实是由隐变量控制的。
再次思考EPRB佯谬，虽然哥本哈根解释已经很好的处理了“信息超光速传递”这一问题，但是仍然无法否定隐变量假说，即无法找到那个控制着粒子坍缩的隐变量，也无法否定它的存在。英国物理学家约翰·贝尔的学生时期玻尔的量子论已经占据了物理学主流的地位，但贝尔更愿意相信波姆对EPR佯谬的化简以及他提出的隐变量假说，因此贝尔致力于设计一套实验，可以证明量子坍缩过程确实是由隐变量控制的。
===贝尔理论的提出===


'''（1）贝尔理论的提出'''
[[File:Bell.png|400px|thumb]]
贝尔在1964年发表的一篇论文中系统的讲述了他的理论：同样考虑一对自旋为1/2的粒子A和B，由于守恒律，，二者自旋方向相反。贝尔选择在不同的方向（沿xyz三个方向）测量自旋为正或为负。用A_x为正来表示在x轴上观测到A粒子自旋为正，用<math>P_{xy}</math>来表示<math>A_x</math>为正和<math>B_y</math>为正的相关性，并给出贝尔不等式：
贝尔在1964年发表的一篇论文中系统的讲述了他的理论：同样考虑一对自旋为1/2的粒子A和B，由于守恒律，，二者自旋方向相反。贝尔选择在不同的方向（沿xyz三个方向）测量自旋为正或为负。用A_x为正来表示在x轴上观测到A粒子自旋为正，用<math>P_{xy}</math>来表示<math>A_x</math>为正和<math>B_y</math>为正的相关性，并给出贝尔不等式：


                                 <math>\left|P_{xy}-P_{zy}\right|\le1+P_{xy}</math>
                                 <math>\left|P_{xy}-P_{zy}\right|\le1+P_{xy}</math>
这是一个对xyz三个方向上观测的相关性的约束，如果这个不等式成立，则表明量子现象是由某个或是某些变量所控制的。贝尔从定域实在性出发，推导出这个不等式的成立，并且给出结论：某些理论为了确定单独测量的结果，严格要求将额外参数加入量子力学，并且要求这动作不改变统计预测。对于这些理论，必定存在一种机制，使得一台测量仪器的运作设定值的改变，会影响到另一台仪器的读数，且这种影响必须瞬间传达，这不符合洛伦兹不变性 。
这是一个对xyz三个方向上观测的相关性的约束，如果这个不等式成立，则表明量子现象是由某个或是某些变量所控制的。贝尔从定域实在性出发，推导出这个不等式的成立，并且给出结论：某些理论为了确定单独测量的结果，严格要求将额外参数加入量子力学，并且要求这动作不改变统计预测。对于这些理论，必定存在一种机制，使得一台测量仪器的运作设定值的改变，会影响到另一台仪器的读数，且这种影响必须瞬间传达，这不符合洛伦兹不变性<ref>Bell, J.S. On the Einstein-Podolosky-Rosen Paradox[J]. Physics, 1, 195-200(1964).</ref>。
===关于验证贝尔不等式的实验===
 
'''（2）关于验证贝尔不等式的实验'''
[[File:Bell2.jpg|350px|thumb]]
贝尔不等式最伟大的地方不在于从定域实在性推出的种种结论，而在于可以用实验验证不等式是否成立，从而彻底的对隐变量假说做出判断。
贝尔不等式最伟大的地方不在于从定域实在性推出的种种结论，而在于可以用实验验证不等式是否成立，从而彻底的对隐变量假说做出判断。


1982年，阿兹派克特（A·Aspect）小组第一次对EPR问题进行精确检验。他们激发钙原子产生激光并将一对光子引导至相距12米的距离，在这个距离上以光速传递信号的时间差约为40ns，控制一对偏振片不断改变方向。通过测量光子不同方向的相关性来检验贝尔不等式是否成立 。实验结果表明，贝尔不等式不成立，隐变量假说几乎被否定。
1982年，阿兹派克特（A·Aspect）小组第一次对EPR问题进行精确检验。他们激发钙原子产生激光并将一对光子引导至相距12米的距离，在这个距离上以光速传递信号的时间差约为40ns，控制一对偏振片不断改变方向。通过测量光子不同方向的相关性来检验贝尔不等式是否成立<ref>A. Aspect, J. Dalibard and G. Roger, Experimental Test of Bell’s Inequalities Using Variable Analyzers[J],Phys. Rev. Lett. 49, 1804 (1982).</ref>。实验结果表明，贝尔不等式不成立，隐变量假说几乎被否定。


但是上述实验仍然存在两个漏洞，首先是定域性漏洞，即两个光子相距不够远，有可能产生光速以内的信号传递，另一个是测量漏洞，受限于光子探测器的效率（约为82.8%），存在测量上的误差。直到2015年，荷兰Delft技术大学的B·Henson研究组在Nature上发表一篇论文，报道了他们利用金刚石色心完成了无漏洞的贝尔不等式验证实验，他们将光子移动到相距1.3km的两个实验室，并将探测效率提升至接近100% 。实验结果依然表明贝尔不等式不成立，从而证伪了定域隐变量假说。根据误差理论分析，实验结果置信度达到96%。这个实验依然存在一些小的不足，例如置信度不够高，测量方向的选择是利用随机数发生器产生的并非完全随机等。要解决这些问题，需要利用人的反应来决定测量方向，也许要更远的实验距离，例如在地月之间进行实验。不过，总的来说，贝尔不等式的验证实验可以基本彻底证伪定域隐变量假说，即在量子力学中，定域实在性是不完全的。
但是上述实验仍然存在两个漏洞，首先是定域性漏洞，即两个光子相距不够远，有可能产生光速以内的信号传递，另一个是测量漏洞，受限于光子探测器的效率（约为82.8%），存在测量上的误差。直到2015年，荷兰Delft技术大学的B·Henson研究组在Nature上发表一篇论文，报道了他们利用金刚石色心完成了无漏洞的贝尔不等式验证实验，他们将光子移动到相距1.3km的两个实验室，并将探测效率提升至接近100%<ref>Hensen, B., Bernien, H., Dréau, A. et al. Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres[J]. Nature 526, 682–686 (2015).</ref>。实验结果依然表明贝尔不等式不成立，从而证伪了定域隐变量假说。根据误差理论分析，实验结果置信度达到96%。这个实验依然存在一些小的不足，例如置信度不够高，测量方向的选择是利用随机数发生器产生的并非完全随机等。要解决这些问题，需要利用人的反应来决定测量方向，也许要更远的实验距离，例如在地月之间进行实验。不过，总的来说，贝尔不等式的验证实验可以基本彻底证伪定域隐变量假说，即在量子力学中，定域实在性是不完全的。


==新的解释==
==新的解释==
===隐变量理论===
下面这个视频展示了哥本哈根学派和多宇宙学派的观点
量子力学的哥本哈根解释认为测量的动作造成了波函数坍缩，从而不可避免地在物理学中引入了“意识”与随机性的存在。这样的物理图景是自牛顿力学以来从未有过的，也自然会有科学家试图引入新的解释来恢复确定且符合因果关系的物理学。
{{#ev:youtube|https://www.youtube.com/watch?v=OjrEudqgZ1M|||||start=0&end=864}}
 
下面这个页面展示了更多解释
对于隐变量理论最初的尝试来源于德布罗意。在1927年的第五次索尔维会议上，他将波函数视为一个处在粒子系统之外的描述，称为导波（pilot wave） ，导波会时刻影响粒子的运动。量子效应表面上的随机性是由一些不可知的变量所造成的，而如果将这些隐藏的变量纳入考虑的范围，则整个系统就可以恢复确定性。1952年，玻姆发展了德布罗意的导波理论，他将后者理论中的“导波”替换成了“量子势”的概念。量子势以粒子为中心弥散在整个空间中，并对周围环境的改变做出探测，以此改变粒子的运动。
 
玻姆发展起来的非定域隐变量理论能够自洽地解释迄今为止的量子现象。但作为恢复物理学“实在性”的代价，隐变量理论放弃了定域性。定域性指不能存在超过光速传播的因果关系，但是玻姆理论中的量子势可以瞬间传回宇宙中任意一处的改变，这种量子超距作用被称为量子纠缠。
 
===系综解释===
玻恩对波函数的诠释指出，波函数的模方代表粒子在空间中该点出现的概率密度，系综解释正是基于这一点所提出的一种对量子力学的解释方法。同样在第五次索尔维会议上，爱因斯坦做的报告提到：若尝试将量子理论描述视为单独系统的完备描述，则这会导致不自然的理论诠释；反言之，若能接受这描述所提到的是很多系统组成的系综，而不是单独系统，则这尝试立刻会变得不必要 。系综解释与哥本哈根解释最大的不同在于，哥本哈根解释认为，任何一个单一态都是对单独系统所作出的完备的描述。而系综解释认为，波函数所描述的不是单个体系的状态，而是多个相同系统（即所谓的“系综”）的统计平均。每一个单一态所做出的预测都是平均的，针对整个粒子集合的。
 
相比于其他的解释，系综解释更像是一种关注技术的现实主义看法。它接受了量子力学的所有数学形式，但是以统计的方式回避了所有对量子力学中随机性的形而上的探讨。系综解释并不试图从任何决定性的概念出发，给出关于量子现象的内禀属性的说明，而只是一种对于量子态的诠释方法。
 
===退相干历史===
退相干历史假说是对哥本哈根解释的继承与发展，有时这种假说也被称为“一致性历史解释”。1984年，美国物理学家罗伯特·格里菲斯发起了一项研究计划，旨在为量子力学的研究提供理论与实验的一致性。这项研究计划最终在其他若干科学家的帮助下，产生了退相干历史解释。


退相干历史解释认为在微观现象中量子概率不具有经典概率的可加性，因为量子事件间存在互相的“干涉”，即量子事件的相干性。但在微观演变至宏观的现象中，由于体系的粒子数急剧增加，量子事件间的干涉项在对所有可能情况遍历累加后相消，这就是退相干的过程。通过这样的解释，退相干历史诠释更为清晰地展示了宏观现象的观测数据与量子现象之间的逻辑等价性。
<big>'''[[more explanation]]'''</big>


==强弱电的统一==
==强弱电的统一==
1926年提出的薛定谔方程是非相对论的，在方程中没有考虑速度的上限。科学家们很自然地想要把这个量子力学的基础与相对论相联系，使量子力学与相对论成为一个兼容的体系。量子力学与狭义相对论的统一在次年很快就由狄拉克方程所完成，在此基础上建立起来的量子场论(QFT)成为一套结合了量子力学，狭义相对论和经典场论的一套自洽的理论。
1926年提出的薛定谔方程是非相对论的，在方程中没有考虑速度的上限。科学家们很自然地想要把这个量子力学的基础与相对论相联系，使量子力学与相对论成为一个兼容的体系。量子力学与狭义相对论的统一在次年很快就由狄拉克方程所完成，在此基础上建立起来的量子场论(QFT)成为一套结合了量子力学，狭义相对论和经典场论的一套自洽的理论。


20世纪20年代，电磁场是唯一已知的经典场，因此基于量子场论，物理学家开始期望统一量子力学与电动力学。在1927年的一篇论文中，狄拉克首先用到了“量子电动力学”一词 。他将真空中的场视作一组量子谐振子，将电磁场，带电粒子与两者间的耦合项共同考虑，成功解释了自发发射，光子散射等现象。量子电动力学认为，两个电荷之间的作用力来源于交换光子。在此框架下，理论预言了反物质的存在，这个预言也在1932年为安德森(Carl Anderson)的实验所证实。然而，在处理氢原子外电子轨道的问题时，理论计算与实验结果存在微小的偏差。为了使理论计算更加精确，物理学家对狄拉克的计算添加了许多微扰项，但是对微扰项进行的任何数学处理最终都会使最终结果趋向无穷大。也就是说，狄拉克的量子电动力学是一个不稳定的模型。在1950年，三组科学家（朱利安·施温格、费曼、弗里曼·戴森和朝永振一郎）分别独立地提出了解决无穷大发散问题的方法。他们采取了一种被称为“重整化”(Renormalization)的方法，对微扰项进行了修正。修正后的计算结果和高精度实验之间的吻合程度在当时是空前的。重整化成功攻破了量子电动力学中无限大的难题。
20世纪20年代，电磁场是唯一已知的经典场，因此基于量子场论，物理学家开始期望统一量子力学与电动力学。在1927年的一篇论文中，狄拉克首先用到了“量子电动力学”一词<ref>P. A. C. Dirac. The quantum theory of the emission and absorption of radiation[J]. DOI:10.1098/rspa.1927.0039</ref>。他将真空中的场视作一组量子谐振子，将电磁场，带电粒子与两者间的耦合项共同考虑，成功解释了自发发射，光子散射等现象。量子电动力学认为，两个电荷之间的作用力来源于交换光子。在此框架下，理论预言了反物质的存在，这个预言也在1932年为安德森(Carl Anderson)的实验所证实。然而，在处理氢原子外电子轨道的问题时，理论计算与实验结果存在微小的偏差。为了使理论计算更加精确，物理学家对狄拉克的计算添加了许多微扰项，但是对微扰项进行的任何数学处理最终都会使最终结果趋向无穷大。也就是说，狄拉克的量子电动力学是一个不稳定的模型。在1950年，三组科学家（朱利安·施温格、费曼、弗里曼·戴森和朝永振一郎）分别独立地提出了解决无穷大发散问题的方法。他们采取了一种被称为“重整化”(Renormalization)的方法，对微扰项进行了修正。修正后的计算结果和高精度实验之间的吻合程度在当时是空前的。重整化成功攻破了量子电动力学中无限大的难题。


在强相互作用力和弱相互作用力被发现后，它们也迅速与量子力学成功交融。1935年，日本物理学家汤川秀树预言，强相互作用力是因为核子交换一种新粒子——介子(meson)而产生的。这种粒子后来被命名为π子，1947年为鲍威尔(Cecil Frank Powell)所发现。1954年，杨振宁和罗伯特·米尔斯对量子电动力学进行推广，从纯理论的角度建立了更复杂的杨-米尔斯理论。这个划时代的理论发现成功导出了量子色动力学以描述强相互作用力。这个名称来源于每种夸克具有不同的“味道”，更有不同的“颜色”。1961年，谢尔登·格拉肖将弱相互作用力和电磁力统一起来考虑，发现电弱相互作用。 1967年，史蒂文·温伯格和阿卜杜勒·萨拉姆将电弱统一理论建立在了杨-米尔斯场论的基础之上，从而得到了一个完美而自洽的理论。与此同时，用于描述所有物质基本粒子的标准模型建成。标准模型中预言的共61种基本粒子，在20世纪中叶后逐渐被实验所证实。2012年，欧洲核子研究组织的大型强子对撞机发现了最后一种基本粒子——希格斯玻色子，宣告标准粒子模型的正确。
在强相互作用力和弱相互作用力被发现后，它们也迅速与量子力学成功交融。1935年，日本物理学家汤川秀树预言，强相互作用力是因为核子交换一种新粒子——介子(meson)而产生的。这种粒子后来被命名为π子，1947年为鲍威尔(Cecil Frank Powell)所发现。1954年，杨振宁和罗伯特·米尔斯对量子电动力学进行推广，从纯理论的角度建立了更复杂的杨-米尔斯理论。这个划时代的理论发现成功导出了量子色动力学以描述强相互作用力。这个名称来源于每种夸克具有不同的“味道”，更有不同的“颜色”。1961年，谢尔登·格拉肖将弱相互作用力和电磁力统一起来考虑，发现电弱相互作用。 1967年，史蒂文·温伯格和阿卜杜勒·萨拉姆将电弱统一理论建立在了杨-米尔斯场论的基础之上，从而得到了一个完美而自洽的理论。与此同时，用于描述所有物质基本粒子的标准模型建成。标准模型中预言的共61种基本粒子，在20世纪中叶后逐渐被实验所证实。2012年，欧洲核子研究组织的大型强子对撞机发现了最后一种基本粒子——希格斯玻色子，宣告标准粒子模型的正确。


至此，四大基本力中的电磁力，强力，弱力均被统一在了量子力学旗下。这种统一了三种基本作用力的理论被称为 “大统一理论”(Grand Unified Theory)。
至此，四大基本力中的电磁力，强力，弱力均被统一在了量子力学旗下。这种统一了三种基本作用力的理论被称为 “大统一理论”[[wikipedia:Grand Unified Theory|Grand Unified Theory]]。


==超弦理论==
==[[wikipedia:string theory|超弦理论]]==
{{#ev:youtube|https://www.youtube.com/watch?v=Da-2h2B4faU|||||start=0&end=480}}
在大统一理论的框架下三种基本作用力得到了统一，但是引力未能纳入统一的理论中，量子力学与广义相对论间的矛盾之处也没有得到调和（在物理本质上两者是相同的）。爱因斯坦晚年一直在进行将四种基本作用力全部统一的尝试，但均以失败告终。
在大统一理论的框架下三种基本作用力得到了统一，但是引力未能纳入统一的理论中，量子力学与广义相对论间的矛盾之处也没有得到调和（在物理本质上两者是相同的）。爱因斯坦晚年一直在进行将四种基本作用力全部统一的尝试，但均以失败告终。


在现有的理论中，最有希望解决这一问题的是发展中的超弦理论。弦论的起点源自意大利物理学家Gabriele Veneziano，他于1968年发现弦图可以描述强相互作用粒子的相互作用，并由此奠定了弦论的基础。用这个模型来描述粒子时等效于描述一根在十维时空中振动的弦，弦的不同振动方式在四维时空中就对应了不同的基本粒子。1971年，物理学家将“超对称”模型引入弦论时发现，弦论所预言的一种全新粒子符合广义相对论，这种粒子能够解释引力的成因。最终，物理学家经过筛查得到了五种自洽的超弦理论。由于无法用实验确定哪种理论是正确的，弦论的发展暂时趋于停滞。
在现有的理论中，最有希望解决这一问题的是发展中的超弦理论。弦论的起点源自意大利物理学家Gabriele Veneziano，他于1968年发现弦图可以描述强相互作用粒子的相互作用，并由此奠定了弦论的基础。用这个模型来描述粒子时等效于描述一根在十维时空中振动的弦，弦的不同振动方式在四维时空中就对应了不同的基本粒子。1971年，物理学家将“超对称”模型引入弦论时发现，弦论所预言的一种全新粒子符合广义相对论，这种粒子能够解释引力的成因。最终，物理学家经过筛查得到了五种自洽的超弦理论。由于无法用实验确定哪种理论是正确的，弦论的发展暂时趋于停滞。


直到1995年，美国科学家爱德华·威腾提出，如果将五种超弦理论中的一个耦合系数放大，最终会出现一个新的维度 。而与此同时，五种理论会趋于一体。换言之，之前科学家发现的五种弦理论本质上是相同的，它们是一个更为基本的理论在不同状况下的极限。5种超弦就都被包容在一个统一的图像中，这个统一的理论被称为“M理论”。M理论也被视为最有可能的终极理论。
直到1995年，美国科学家爱德华·威腾提出，如果将五种超弦理论中的一个耦合系数放大，最终会出现一个新的维度<ref>Edward Witten. String Theory Dynamics In Various Dimensions[J]. Nuclear Physics B. 443 (1): 85–126.DOI:10.1016/0550-3213(95)00158-O</ref>。而与此同时，五种理论会趋于一体。换言之，之前科学家发现的五种弦理论本质上是相同的，它们是一个更为基本的理论在不同状况下的极限。5种超弦就都被包容在一个统一的图像中，这个统一的理论被称为“M理论”。M理论也被视为最有可能的终极理论。


然而根据弦论，弦的长度非常小，要使如此微观的结构暴露出来，需要现今人类所无法获得的极高能量，迄今为止尚未有实验数据能够证实或证伪超弦理论与M理论。
然而根据弦论，弦的长度非常小，要使如此微观的结构暴露出来，需要现今人类所无法获得的极高能量，迄今为止尚未有实验数据能够证实或证伪超弦理论与M理论。


=='''范畴论意义下的量子信息'''==
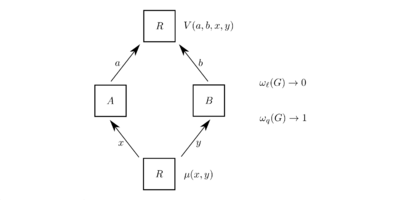
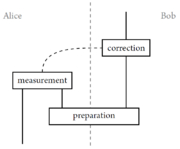
在考虑量子信息时，我们考虑右边这样一幅图
[[File:0.png|180px|thumb]]
纵向表示时间，横向表示空间。量子信息关心的“时间”和“空间”是什么？“空间”，也就是想表达，Alice和Bob的操作是只影响他们自己的系统，还是整个系统；“时间”就是想表达，操作的先后关系。所以真正重要的只是这个图的连通结构。'''这和时空锥所描述的是一致的。'''
[[File:Lightcone.png|400px|thumb]]
可以将时间轴上的线段看成恒等态射，空间轴上并排可以由张量积描述，这是一个幺半范畴。
===范畴的基本组成===
范畴的基本组成是对象和它们间的态射，态射自然有结合律，也自然地有对象到自身的恒等态射，事实上这个态射正可以看作对象本身。范畴能涵盖的事物广若天际：可以是数学中的结构与保结构映射，可以是物理系统与过程，可以是数据类型与算法，可以是逻辑命题与蕴含。
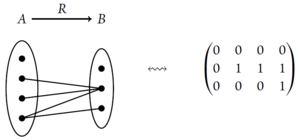
最简单的自然是由集合与函数组成的范畴Set，如果将它看作物理系统，那么完全是经典的，因为对一个<math>a\in A</math>，函数<math>f</math>只选择相应的一个<math>f(a)\in B</math>，这就相当于，<math>A</math>中的一个元素确定地演化成<math>B</math>中的一个元素。定义两个集合之间的多个元素与多个元素之间的关系<math>A\to B</math>，这同矩阵的乘法规则是一样的，我们当然可以用矩阵乘法来表述
[[File:Quan1.png|thumb]]
这样就将关系从一维变成了多维
[[wikipedia:Monoidal category|幺半范畴]]带上了张量积<math>\otimes</math>，这样就能描述并排的，而不只是依次发生的过程。一个很自然的问题：<math>(A\otimes B)\otimes C</math>和 <math>A\otimes (B\otimes C)</math>是什么关系？物理上显然是一回事，不过我们知道，如果<math>\otimes</math>是Hilbert空间上的张量积，那严格来说并不相等，只是同构，不过在范畴论中这就够了。
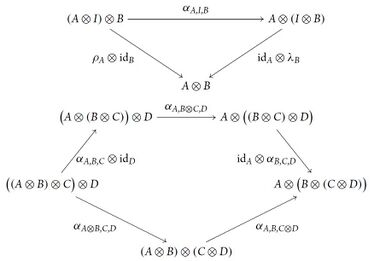
张量积的运算满足下面的三角形和五边形法则
[[File:Quan2.jpg|380px|thumb]]
===态射和对象===
在范畴论中，我们要用态射来想问题，忘记对象。于是对象<math>A</math>的态定义成态射<math>A\to I</math>，这其实就是让系统<math>A</math>从什么都没有中出现。为了强调态的定义域是<math>I</math>，我们用三角形表示它：
为什么纠缠是量子力学中才有的东西？不妨想一下完全经典的Set，它的张量积就是直积，那么在张量积空间中根本不可能有无法表示成张量积的态。而在半经典的Rel中，张量积比直积要满足更多的条件，纠缠态是存在的。更多物理的讨论在[[https://zhuanlan.zhihu.com/p/34562677]]中
=='''结语—范式转换与范畴论'''==
量子力学自诞生至今一百余年，已经发展为最成功的理论体系之一，经历三个大的时期，十几个范式的转换，根据上文的描述，量子力学范式转换被表示为这样一张有向箭头图。量子力学范式转换的根本动力是不断观测到新的现象，在几十年的发展后量子力学最终形成了完整的理论，正如最后一部分所讲这个理论的核心也是范畴论——即单子和单子、系统和系统之间的有向关系。
</big>
</big>
[[File:Fig1.png|thumb|400px|History]]
==参考文献==
[[Category:TDCF2021]]
{{#set:
Has Topic={{PAGENAME}}
|Author=于舒昂
}}

Latest revision as of 03:45, 15 December 2021

Error creating thumbnail: Unable to save thumbnail to destination
History

用偏序集描述量子力学中的范式转换

本文从范畴论的角度梳理了量子力学发展的三个范式阶段：前范式时期，矩阵力学与波动力学对立时期，统一理论时期。细节的范式转换被表示在上面这幅图中，可以看出整个范式转换可以被偏序集刻画的。

早期量子论

在量子力学建立二十余年之前，随着赫兹证明了电磁波的存在与玻尔兹曼建立统计物理学，整个物理学形成了一套自洽的体系。以经典力学，经典电磁理论与经典热力学，统计物理学三大学科作为支柱的物理学，已经能够解释现实世界中几乎一切现象。在这样的背景下，1900年，开尔文勋爵做了一篇著名的关于未来物理学展望的报告：《在热和光动力理论上空的19世纪乌云》[1]。在这篇报告中，开尔文勋爵提到了当时物理学界运用已有的知识无法解决的两大问题，并将其称为两朵乌云。这两朵乌云一是迈克尔逊-莫雷实验所测得的地球相对以太速度为零，二是黑体辐射理论与实验的不一致。这两个问题直接引发了二十世纪物理理论的革命。第一个问题导致了狭义相对论的诞生，而第二个问题导致了量子力学的建立。 {{#ev:youtube|https://www.youtube.com/watch?v=i1TVZIBj7UA%7C%7C%7C%7C%7Cstart=0&end=259}}

下面这个页面展示了经典物理学面临的危机。从而引发科学革命的范式转换。

Paradigm shift

新的问题

除此之外，崭新的量子论面临着更大的问题。。1925年，为了解释谱线在在弱磁场下的一种复杂分裂——“反常塞曼效应”，科学家提出了电子自旋理论，然而这种理论要求引入一个1/2的量子数[2]，这是玻尔模型所没有给出预测的。同时，玻尔也发现了他的理论只能解决单电子的原子，如氢原子，一级电离的氦原子。然而，对多电子原子，玻尔模型无法给出任何有用的结论。

玻尔是立足于经典物理理论建立原子模型的。在从经典到量子的转化过程中，玻尔理论不能解释为何在宏观条件下成立的经典理论，在围观的原子层面就必须加入量子化的条件。玻尔的理论终究只是经典理论向量子模型所做出的妥协。实验表明，旧量子论这一基于经典理论的修正无法解释所有的物理现象，物理学必须要有一个崭新的范式作为基石继续前进。

量子体系的完善

在第一部分中，我们讲述了量子力学出现的背景和早期量子论的种种尝试，但是诸如玻尔原子模型这样的理论是很难作为一个新的范式而指导下一个阶段的研究工作的，因为它还不够成熟，过多的应用了一些强制的“规定”，给电子赋予了过多的“特有性质”而失去了一般性。在这一部分中，我们将详细的研究科学家们是如何建立一个相对完善的体系的。

（1）矩阵力学的建立

德布罗意在了解玻尔原子模型之后企图通过引入一种周期性来解释角动量量子化。在1919-1921年，布里渊曾发表过一系列论文，阐述了电子在运动时激发周围的以太形成的一种波动。德布罗意没有从以太的角度出发而结合了相对论，将粒子从波的角度考虑，得到：

并且大胆预言，电子存在一个内禀的频率，在运动时会伴随一个波，这个波的波速为：

不难发现这个速度是有可能大于光速的，但是由于这个波不携带能量和信息，因此不违反相对论。德布罗意大胆的预言在1927年被戴维逊和革末所证实，他们在用电子束轰击金属镍时得到了与x射线衍射几乎一样的结果，从而证明了电子的波动性。

电子波动性的证实使得危机空前严重，也进一步推动了革命的进行。1920年海森堡开始研究反常塞曼效应并提出半整数量子数的解释，当时并未得到认可。1924-1925年间，他加入了克拉摩斯研究色散理论的团队，他发现原子理论中的轨道应当被一种更好的观点所代替[3]，与此同时，他的研究方式开始脱离开物理模型而直接建立数学模型。

1925年海森堡开始研究氢原子光谱的问题，他受到BKS理论和玻尔对应理论的影响，确立了研究的出发点：“物理学应当从一些可以直接被实验观察和检验的物理量出发 ”[4]，由此他放弃了轨道等经典概念来想象原子，只把光谱提供的具体数据作为工作对象，他提出了一种“表格”式的数学规则来表示原子吸收、发射辐射的过程。在把他的研究成果和玻恩交流后，玻恩才意识到这种“表格”就是已经被数学家所发明的矩阵。1925年9月，海森堡在《物理学报》上论文的发表，标志着矩阵力学的建立，同时由于他的理论物理意义不够清晰，因此并没能得到很多人的认可。在此之后，狄拉克发现用泊松括号[x,y]作用于经典哈密顿函数上，就得到了和海森堡矩阵形式完全一样的结论。3个月之后，海森堡用矩阵处理了自旋问题，很好的得到了半整数量子数的结果，并且将自旋作为电子的一种属性，避免了自旋经典解释中的种种问题。至此，一个新的研究范式已经初步建成。

（2）波动力学的建立

薛定谔于1922年开始在苏黎世大学任教，在1925年的大部分时间里，他仍在研究理想气体的量子统计问题，在与爱因斯坦的来往中得知了德布罗意的论文。他认为德布罗意在对量子规则的解释上与自己有相同之处。在德拜主持的一个讨论会上，薛定谔做了一个漂亮的报告，清晰地阐述了德布罗意如何给粒子配上一列波[5]，德拜对于他只用几何图像来解释量子规则感到不满，德拜认为“讨论波的性质，必须要有一个波动方程”，从而促使薛定谔着手于研究波动方程。

薛定谔最先着手于相对论性波动方程的研究，但结果与索末菲方程不一致因此失败。1926年初，他开始考虑非相对论性的波动方程，不到半年，就在Annalen der Physik杂志上发表了Quantisierung als Eigenw ertproblem第一、二、三、四部分论文，奠定了波动力学的基础。

薛定谔通过对经典哈密顿-雅可比方程进行一个变量代换并对空间做积分变分，从而得到了一个波动方程，也就是定态的薛定谔方程。

在第一部分论文中，对于氢原子求解了本征值，得到了角向是球谐函数，径向与玻尔原子论符合的很好。在后续的几篇文章中，又成功地把波动理论推广到了含时微扰并解决了色散问题，得到了一般形式下的波动方程。

{{#ev:youtube|https://www.youtube.com/watch?v=TQKELOE9eY4%7C%7C%7C%7C%7Cstart=0&end=283}}

（3）不确定性

海森堡所使用的矩阵存在一个独特的性质，即矩阵的乘）法一般情况下是不可交换的即

这也就说明，位置（矩阵）乘以动量（矩阵）不等于动量（矩阵）乘以位置（矩阵），这促使海森堡意识到任意两个不对易的物理量之间的测量顺序会影响测量结果，也就是说p和q会相互影响，即存在一种不确定性关系（Uncertain Principle）

这并非由于仪器的误差导致，而是粒子本身的性质所导致的

矩阵形式和波动形式的统一

两种形式的争论

在1926年薛定谔发表四部分文章的间隙中就已经证明了两种表述形式在数学上的一致性，同一时期，泡利，约尔当也各自证明了其等价性。但是两种竞争着的范式并没有因此而统一，争论还在进行。作为理论在数学上已经统一，但作为两种范式，在物理图像和对物理现象的解释上还存在巨大的分歧，也就是说还是不可通约的。回顾这两个范式在刚刚诞生时期的状况，矩阵力学直接以可观测的量为基础，强调数学导向而非经验式的构建物理图像，在解释自旋等问题上有很出色的表现，但是由于矩阵形式的晦涩和物理图像不清晰，没有得到大多数科学家的追随。波动力学从德布罗意理论出发，由于其数学形式接近于经典，因此得到了大多数科学家的追随，但是同样面临着物理意义不清晰的问题，在很长一段时间内都无法解释的物理含义，只能含糊其词为一种尚没有观测到的分布。更严重的问题在于波恩在解释的物理意义时引入了概率，坍缩等一系列与经典格格不入的概念，因而招致了爱因斯坦等科学家甚至是薛定谔本人的反对，这一部分将在后续进一步讨论。

电子双缝实验

量子力学的发展

对量子现象的解释

随着矩阵力学和波动力学的统一、不确定性关系的提出和互补原理的提出，量子力学完善的范式已经基本建成，但新的危机立刻就产生了，即如何对复杂的理论加以物理图像上的清晰的解释。较为主流的一个学派是以不确定性和互补原理为主要理论，对量子现象加以概率解释的“哥本哈根”解释，这一解释的拥护者主要有玻尔、海森堡、泡利、约尔当等人。这一解释体系最大的反对者是保守地相信经典物理因果律关系的学派，以爱因斯坦为领导。值得一提，薛定谔虽然是波动力学的奠基人，但是他却不相信概率解释，而是因果律的坚定拥护者。

由于哥本哈根解释是目前比较主流的一种解释，因此本文将以之为主体来讲述因果律派与哥本哈根派的争论过程，并在最后介绍几种其它的量子现象的解释。下面这个视频讲述了哥本哈根学派的诞生

{{#ev:youtube|https://www.youtube.com/watch?v=-HJhKuM-jX4%7C%7C%7C%7C%7Cstart=0&end=960}}

（1）哥本哈根解释的基本内容

哥本哈根解释是以不确定性原理、互补原理和概率解释三者为主体所建立的。不确定性原理和互补原理表明，一个微观客体展现出什么样的性质是由我们以何种方式观测它所决定的，也就是说单独去谈论一个微观客体具有什么样的性质是没有意义的。这样的解释推翻了经典物理中的完全客观性。一个体系可以完全由波函数描述，在没有对一个量子体系观测的时候，量子体系按照薛定谔方程发展演化，这时候的体系是多个状态的叠加态，当我们对体系进行观测，波函数发生了坍缩，坍缩的过程具有随机性和不可逆性，也就是说体系从多个状态的叠加态变成了一个确定的状态。对于薛定谔方程中的意义，哥本哈根派不认为波函数有除了抽象的概念以外的任何真实存在，也就是说波函数不代表一个实体，当波函数按照一定的概率坍缩之后才能够代表一个实体。如果去探究在观测之前、坍缩之前的电子是什么状态、在哪个位置，哥本哈根解释中最不可思议的地方就展现出来：在观测（也就是波函数坍缩）之前，电子是没有意义的，不具有客观性和实在性，也就是说，真实存在的不是电子，而是“观测者观测电子”这一相互作用[6]。

（2）爱因斯坦的观点

爱因斯坦反对哥本哈根解释的主要原因有以下两点：

一方面，爱因斯坦相信因果律在物理学中是根本性的原理，而波函数根据概率分布坍缩这一过程体现了强烈的随机性和不可逆性，这和爱因斯坦所在的研究范式的不可通约的。

另一方面，电子坍缩这一过程意味着电子可以在很短的时间内改变自己的位置（这也是不确定性原理所告诉我们的），在量子纠缠中也似乎存在违反定域性的现象，这似乎代表着一种超距作用，这是不符合相对论的。

玻尔-爱因斯坦的伟大辩论

这一阶段爱因斯坦和玻尔的争论是物理学史上最著名的辩论之一,从1927年第五届索尔维会议开始，两位科学家一直在进行关于量子体系完备性的争论。接下来这一部分将给出几个例子来构建争论的过程和量子力学体系的进一步完善。这些例子不仅体现了物理学家敏锐的洞察力和犀利的思维，也能够很好的诠释库恩的理论——范式具有不可通约性、在新的范式面前，很少有科学家能够由旧的范式“改宗”至新的范式。

下面，通过几个例子来展现物理学史上最伟大的思想碰撞

Some interesting thought experiments

贝尔不等式

定域性的范畴表述

再次思考EPRB佯谬，虽然哥本哈根解释已经很好的处理了“信息超光速传递”这一问题，但是仍然无法否定隐变量假说，即无法找到那个控制着粒子坍缩的隐变量，也无法否定它的存在。英国物理学家约翰·贝尔的学生时期玻尔的量子论已经占据了物理学主流的地位，但贝尔更愿意相信波姆对EPR佯谬的化简以及他提出的隐变量假说，因此贝尔致力于设计一套实验，可以证明量子坍缩过程确实是由隐变量控制的。

（1）贝尔理论的提出

Bell.png

贝尔在1964年发表的一篇论文中系统的讲述了他的理论：同样考虑一对自旋为1/2的粒子A和B，由于守恒律，，二者自旋方向相反。贝尔选择在不同的方向（沿xyz三个方向）测量自旋为正或为负。用A_x为正来表示在x轴上观测到A粒子自旋为正，用来表示为正和为正的相关性，并给出贝尔不等式：

这是一个对xyz三个方向上观测的相关性的约束，如果这个不等式成立，则表明量子现象是由某个或是某些变量所控制的。贝尔从定域实在性出发，推导出这个不等式的成立，并且给出结论：某些理论为了确定单独测量的结果，严格要求将额外参数加入量子力学，并且要求这动作不改变统计预测。对于这些理论，必定存在一种机制，使得一台测量仪器的运作设定值的改变，会影响到另一台仪器的读数，且这种影响必须瞬间传达，这不符合洛伦兹不变性[7]。

（2）关于验证贝尔不等式的实验

Bell2.jpg

贝尔不等式最伟大的地方不在于从定域实在性推出的种种结论，而在于可以用实验验证不等式是否成立，从而彻底的对隐变量假说做出判断。

1982年，阿兹派克特（A·Aspect）小组第一次对EPR问题进行精确检验。他们激发钙原子产生激光并将一对光子引导至相距12米的距离，在这个距离上以光速传递信号的时间差约为40ns，控制一对偏振片不断改变方向。通过测量光子不同方向的相关性来检验贝尔不等式是否成立[8]。实验结果表明，贝尔不等式不成立，隐变量假说几乎被否定。

但是上述实验仍然存在两个漏洞，首先是定域性漏洞，即两个光子相距不够远，有可能产生光速以内的信号传递，另一个是测量漏洞，受限于光子探测器的效率（约为82.8%），存在测量上的误差。直到2015年，荷兰Delft技术大学的B·Henson研究组在Nature上发表一篇论文，报道了他们利用金刚石色心完成了无漏洞的贝尔不等式验证实验，他们将光子移动到相距1.3km的两个实验室，并将探测效率提升至接近100%[9]。实验结果依然表明贝尔不等式不成立，从而证伪了定域隐变量假说。根据误差理论分析，实验结果置信度达到96%。这个实验依然存在一些小的不足，例如置信度不够高，测量方向的选择是利用随机数发生器产生的并非完全随机等。要解决这些问题，需要利用人的反应来决定测量方向，也许要更远的实验距离，例如在地月之间进行实验。不过，总的来说，贝尔不等式的验证实验可以基本彻底证伪定域隐变量假说，即在量子力学中，定域实在性是不完全的。

新的解释

下面这个视频展示了哥本哈根学派和多宇宙学派的观点 {{#ev:youtube|https://www.youtube.com/watch?v=OjrEudqgZ1M%7C%7C%7C%7C%7Cstart=0&end=864}} 下面这个页面展示了更多解释

more explanation

强弱电的统一

1926年提出的薛定谔方程是非相对论的，在方程中没有考虑速度的上限。科学家们很自然地想要把这个量子力学的基础与相对论相联系，使量子力学与相对论成为一个兼容的体系。量子力学与狭义相对论的统一在次年很快就由狄拉克方程所完成，在此基础上建立起来的量子场论(QFT)成为一套结合了量子力学，狭义相对论和经典场论的一套自洽的理论。

20世纪20年代，电磁场是唯一已知的经典场，因此基于量子场论，物理学家开始期望统一量子力学与电动力学。在1927年的一篇论文中，狄拉克首先用到了“量子电动力学”一词[10]。他将真空中的场视作一组量子谐振子，将电磁场，带电粒子与两者间的耦合项共同考虑，成功解释了自发发射，光子散射等现象。量子电动力学认为，两个电荷之间的作用力来源于交换光子。在此框架下，理论预言了反物质的存在，这个预言也在1932年为安德森(Carl Anderson)的实验所证实。然而，在处理氢原子外电子轨道的问题时，理论计算与实验结果存在微小的偏差。为了使理论计算更加精确，物理学家对狄拉克的计算添加了许多微扰项，但是对微扰项进行的任何数学处理最终都会使最终结果趋向无穷大。也就是说，狄拉克的量子电动力学是一个不稳定的模型。在1950年，三组科学家（朱利安·施温格、费曼、弗里曼·戴森和朝永振一郎）分别独立地提出了解决无穷大发散问题的方法。他们采取了一种被称为“重整化”(Renormalization)的方法，对微扰项进行了修正。修正后的计算结果和高精度实验之间的吻合程度在当时是空前的。重整化成功攻破了量子电动力学中无限大的难题。

在强相互作用力和弱相互作用力被发现后，它们也迅速与量子力学成功交融。1935年，日本物理学家汤川秀树预言，强相互作用力是因为核子交换一种新粒子——介子(meson)而产生的。这种粒子后来被命名为π子，1947年为鲍威尔(Cecil Frank Powell)所发现。1954年，杨振宁和罗伯特·米尔斯对量子电动力学进行推广，从纯理论的角度建立了更复杂的杨-米尔斯理论。这个划时代的理论发现成功导出了量子色动力学以描述强相互作用力。这个名称来源于每种夸克具有不同的“味道”，更有不同的“颜色”。1961年，谢尔登·格拉肖将弱相互作用力和电磁力统一起来考虑，发现电弱相互作用。 1967年，史蒂文·温伯格和阿卜杜勒·萨拉姆将电弱统一理论建立在了杨-米尔斯场论的基础之上，从而得到了一个完美而自洽的理论。与此同时，用于描述所有物质基本粒子的标准模型建成。标准模型中预言的共61种基本粒子，在20世纪中叶后逐渐被实验所证实。2012年，欧洲核子研究组织的大型强子对撞机发现了最后一种基本粒子——希格斯玻色子，宣告标准粒子模型的正确。

至此，四大基本力中的电磁力，强力，弱力均被统一在了量子力学旗下。这种统一了三种基本作用力的理论被称为 “大统一理论”Grand Unified Theory。

超弦理论

{{#ev:youtube|https://www.youtube.com/watch?v=Da-2h2B4faU%7C%7C%7C%7C%7Cstart=0&end=480}} 在大统一理论的框架下三种基本作用力得到了统一，但是引力未能纳入统一的理论中，量子力学与广义相对论间的矛盾之处也没有得到调和（在物理本质上两者是相同的）。爱因斯坦晚年一直在进行将四种基本作用力全部统一的尝试，但均以失败告终。

在现有的理论中，最有希望解决这一问题的是发展中的超弦理论。弦论的起点源自意大利物理学家Gabriele Veneziano，他于1968年发现弦图可以描述强相互作用粒子的相互作用，并由此奠定了弦论的基础。用这个模型来描述粒子时等效于描述一根在十维时空中振动的弦，弦的不同振动方式在四维时空中就对应了不同的基本粒子。1971年，物理学家将“超对称”模型引入弦论时发现，弦论所预言的一种全新粒子符合广义相对论，这种粒子能够解释引力的成因。最终，物理学家经过筛查得到了五种自洽的超弦理论。由于无法用实验确定哪种理论是正确的，弦论的发展暂时趋于停滞。

直到1995年，美国科学家爱德华·威腾提出，如果将五种超弦理论中的一个耦合系数放大，最终会出现一个新的维度[11]。而与此同时，五种理论会趋于一体。换言之，之前科学家发现的五种弦理论本质上是相同的，它们是一个更为基本的理论在不同状况下的极限。5种超弦就都被包容在一个统一的图像中，这个统一的理论被称为“M理论”。M理论也被视为最有可能的终极理论。

然而根据弦论，弦的长度非常小，要使如此微观的结构暴露出来，需要现今人类所无法获得的极高能量，迄今为止尚未有实验数据能够证实或证伪超弦理论与M理论。

范畴论意义下的量子信息

在考虑量子信息时，我们考虑右边这样一幅图

0.png

纵向表示时间，横向表示空间。量子信息关心的“时间”和“空间”是什么？“空间”，也就是想表达，Alice和Bob的操作是只影响他们自己的系统，还是整个系统；“时间”就是想表达，操作的先后关系。所以真正重要的只是这个图的连通结构。这和时空锥所描述的是一致的。

Lightcone.png

可以将时间轴上的线段看成恒等态射，空间轴上并排可以由张量积描述，这是一个幺半范畴。

范畴的基本组成

范畴的基本组成是对象和它们间的态射，态射自然有结合律，也自然地有对象到自身的恒等态射，事实上这个态射正可以看作对象本身。范畴能涵盖的事物广若天际：可以是数学中的结构与保结构映射，可以是物理系统与过程，可以是数据类型与算法，可以是逻辑命题与蕴含。

最简单的自然是由集合与函数组成的范畴Set，如果将它看作物理系统，那么完全是经典的，因为对一个，函数只选择相应的一个，这就相当于，中的一个元素确定地演化成中的一个元素。定义两个集合之间的多个元素与多个元素之间的关系，这同矩阵的乘法规则是一样的，我们当然可以用矩阵乘法来表述

Quan1.png

这样就将关系从一维变成了多维

幺半范畴带上了张量积，这样就能描述并排的，而不只是依次发生的过程。一个很自然的问题：和 是什么关系？物理上显然是一回事，不过我们知道，如果是Hilbert空间上的张量积，那严格来说并不相等，只是同构，不过在范畴论中这就够了。

张量积的运算满足下面的三角形和五边形法则

Quan2.jpg

态射和对象

在范畴论中，我们要用态射来想问题，忘记对象。于是对象的态定义成态射，这其实就是让系统从什么都没有中出现。为了强调态的定义域是，我们用三角形表示它： 为什么纠缠是量子力学中才有的东西？不妨想一下完全经典的Set，它的张量积就是直积，那么在张量积空间中根本不可能有无法表示成张量积的态。而在半经典的Rel中，张量积比直积要满足更多的条件，纠缠态是存在的。更多物理的讨论在[[1]]中

结语—范式转换与范畴论

量子力学自诞生至今一百余年，已经发展为最成功的理论体系之一，经历三个大的时期，十几个范式的转换，根据上文的描述，量子力学范式转换被表示为这样一张有向箭头图。量子力学范式转换的根本动力是不断观测到新的现象，在几十年的发展后量子力学最终形成了完整的理论，正如最后一部分所讲这个理论的核心也是范畴论——即单子和单子、系统和系统之间的有向关系。

Error creating thumbnail: Unable to save thumbnail to destination
History

参考文献

  1. ↑ Kelvin, Lord. Nineteenth century clouds over the dynamical theory of heat and light[J]. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science,1901,2(7).
  2. ↑ G. E. Uhlenbeck, S. Goudsmit. Ersetzung der Hypothese vom unmechanischen Zwang durch eine Forderung bezüglich des inneren Verhaltens jedes einzelnen Elektrons[J]. Naturwissenschaften,1925.
  3. ↑ 大卫·C·卡西第.海森堡传[M].戈革译,商务印书馆,2002.
  4. ↑ 曹天元.上帝掷骰子吗?量子物理史话[M].辽宁:辽宁教育出版社,2011.5.
  5. ↑ 赵凯华.创立量子力学的睿智才思——纪念矩阵力学和波动力学诞生80~81周年[J].大学物理,2006(09):1-9.
  6. ↑ Everett·Hugh. Relative State Formulation of Quantum Mechanics[J]. Reviews of Modern Physics. 1957, 29: 454–462.
  7. ↑ Bell, J.S. On the Einstein-Podolosky-Rosen Paradox[J]. Physics, 1, 195-200(1964).
  8. ↑ A. Aspect, J. Dalibard and G. Roger, Experimental Test of Bell’s Inequalities Using Variable Analyzers[J],Phys. Rev. Lett. 49, 1804 (1982).
  9. ↑ Hensen, B., Bernien, H., Dréau, A. et al. Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres[J]. Nature 526, 682–686 (2015).
  10. ↑ P. A. C. Dirac. The quantum theory of the emission and absorption of radiation[J]. DOI:10.1098/rspa.1927.0039
  11. ↑ Edward Witten. String Theory Dynamics In Various Dimensions[J]. Nuclear Physics B. 443 (1): 85–126.DOI:10.1016/0550-3213(95)00158-O
Retrieved from "https://pkc.pub/index.php?title=范畴论下量子力学的范式转换&oldid=19510"