现代遗传学

Logic Model (结题作业) Template:LogicModel 12 12, 2021
Abstract Specification Context 接下来将以遗传学为例探究学科认知的共同性。遗传学是研究生物代际信息传递的学科。遗传学在历史上共发生了三次重大的范式转变。第一次是从前范式时期到孟德尔遗传学；第二次是从孟德尔的颗粒遗传学到经典遗传学；第三次是从经典遗传学发展到与分子生物学、生物化学结合的现代遗传学。 Goal 蒋玉骅“超越学科的认知基础”课程主页 课程感悟 科学革命的结构读后感 Success Criteria 第一：范式所揭示的事物之本质 第二：虽普遍但较少的事实判定（边界条件） 第三：与实证数据相匹配的范式 第四：选择问题的标准（可建模） 第五：规则的抽象化（通用性） 第六：解答谜题所需的空间与时间
Concrete Implementation Given Inputs When Process is executed... Then, we get Outputs 1、《科学革命的结构》这本书会使我对学科的发展有新的认知； 2、在课程中所学习的新的概念和新的思维方式也将会使我对跨越学科的问题有新的认知。 遗传学的前范式时代 孟德尔遗传学 经典遗传学 现代遗传学 1、设计个人主页； 2、Final Project 3、《科学革命的结构》读后感
Boundary/Safety Conditions of 结题作业 1、有时课堂上所学的一些概念难以在短时间内准确理解； 2、有时难以看懂老师提供的英文资料，很难明白想要表达的意思。

Final Project

开题报告

理想的偏序集

Error creating thumbnail: Unable to save thumbnail to destination

沃森和克里克的“量子”——遗传因子

作为一个复杂程度极高的系统，遗传学在孟德尔之前并未形成确定的范式，本质原因是因为没有人找到这个复杂系统的度量衡单位。孟德尔定义了遗传学的“量子”——“遗传因子”，自此遗传学成为了一个可表达（Representable）的系统。在孟德尔的会计方式下，每个可证明的结论都是正确的，从而具备了可靠性（Soundness）；每个正确的结论都是可被证明的，从而具备了完备性（Completeness）

孟德尔的“量子”——遗传因子

作为孟德尔的话语体系中的“量子”，“遗传因子”扮演了计算机的话语体系中的比特的角色，“遗传因子”有显性和隐形，对应了比特为0或1。但问题随之出现：这样的语言所建立的偏序集并不能趋近遗传系统的各类结构。

于是才产生了科学革命，“量子”的转变标志着范式的更替。自1953年沃森（J.D.Watson）和克里克（F.H.C.Crick）发现了DNA的双螺旋结构后，遗传学的“量子”由遗传因子变成了碱基对。令人惊奇的是，新的“量子”碱基对也恰有两类：“A-T”“C-G”碱基对的相互影响作用构成了基因这个偏序集，而遗传学的重心变成了破译函子——将基因映射到表现型的函子。这被后人称为中心法则。

简介

遗传学系统模型的优化是一个反复迭代的模型空间搜寻过程，这在前范式阶段得到了充分的体现。在孟德尔之前，遗传学并未形成确定的范式，而是处于前范式时期。对遗传的认识主要来源于对自然界的观察、农业实践和畜牧业实践。这一时期，相竞争的范式主要是模子学说、蓝图学说、融合遗传学说（Blending inheritance）与获得性遗传学说。这四种学说的产生时期不同、关注点也不同，体现了前范式时期较为典型的特征。

孟德尔(Mendel)的出现增加了遗传学知识的可表达性，甚至是遗传学计算的连续性（即使使用了类似箭头的符号）。孟德尔开创的的遗传学知识都可以使用相应的箭头来进行描述,从而构建相应的框架.使逻辑模型可进行知识表达(详见[1])。

遗传学的前范式时代

从范畴学的角度看，遗传学系统模型的优化是一个反复迭代的模型空间搜寻过程，这在前范式阶段得到了充分的体现。模子学说是由希波克拉底提出的，他认为后代的成长就是在逐渐接近父本的模子。然而，亚里士多德基于他的理念哲学和生活观察，提出了蓝图学说，即父代与子代有发展成相同形态的能力。获得性遗传由拉马克提出，是为了解释地层中发现的物种演化现象。融合遗传学说则是由达尔文提出。1859年达尔文在著作《物种起源》一书中提出了以自然选择为中心的进化学说，确立了变异、遗传和选择是生物进化的基本因素。其中的遗传指的就是融合遗传。然而达尔文并不了解三者之间相互联系的机制，更无法回答变异的来源和维持机理。《物种起源》发表后，生物进化理论虽然很快被学术界所承认，但不久又遭到种种非难，其中主要是所谓杂交淹没效应。

1867年英国数学家兼工程师詹金，从融合遗传理论出发，根据简单的数学计算，认为如果以突变的形式产生新的变异，因其数量有限，单个突变个体同大量正常者交配，以后便会淹没在正常个体里，变异逐渐减弱，终至完全消失，使自然选择无能为力。因此通过选择累积作用而产生进化是难以置信的。詹金对《物种起源》的这种批评使达尔文十分烦恼，穷于应付。

事实上达尔文创建了一个可表函子,也就是一种可以穿透多层次系统的数据映射机制。在那个时代，达尔文的融合遗传理论十分流行。人们把遗传物质猜测为液体状态的东西，认为任何一个个体都是双亲液体遗传物质相互融合的产物。两种液体一旦融合，各自所具有的特性均被冲淡，最后使变异丧失净尽。对此达尔文也将信将疑。为了让自己的进化学说与融合遗传理论相互协调，他不得不改变原来对突变的看法，主张必须拥有大量的一定变异（不遗传的变异）即大量个体之间的差异，方能给自然选择提供材料，物种才得以进化。同时达尔文在《豢养和栽培下动植物的变异》一书中增加了《外界条件的直接作用和一定作用》、《器官的训练与不训练》两章，同时提出泛生说以解释获得性状的遗传现象。达尔文不懂遗传学的内在规律，不明白遗传在物种进化中的作用而改变了自己的观点，其后果是严重的。此后，遗传学家契特维雷科夫指出：这一改变使他对基因突变作用和意义的看法与现代遗传学距离越来越远；这一改变使他更加接近拉马克主义，。根源在于没有吸收同时代人的科学成果，反而坚持融合遗传理论。杜勃赞斯基认为要是达尔文“放弃了融合遗传理论，他就把阻碍进化思想前进的道路打通了”。吸收和放弃的可能性与条件都是存在的，然而对达尔文来说，都没有成为现实。

孟德尔遗传学

以偏序集观点来看，融合遗传学说注定是没有发展前途的，因为它违背了一个信息传递的基本原则，也就是所有的数据均可用可表函子，也就是有向关系的数据结构来编码与计算。换言之，可表函子提供了一个形式化的数学表达方式来提供库恩的科学范式的拓展范式。因此，不能用可表函子来编码与计算的融合遗传学就不能提供一个具备可靠性（soundness）和完备性(completeness)的范式。

1866年，孟德尔的论文《植物杂种实验》的发表奠定了遗传的基本规律，揭开了现代遗传学的历史。然而，孟德尔论文在当时并未被学界所熟知，达尔文在提出进化论时对孟德尔的研究结果一无所知，而孟德尔在进行实验时《物种起源》还未问世，由此可见，孟德尔所提出的前范式有达尔文的进化论时独立发生的。孟德尔的论文直到1900年才由德弗里斯等科学家再次发现，他们重复了他的实验，得到了相近的结果。此时孟德尔遗传学真正地作为一种前范式加入前范式竞争并很快地为学界所接受。

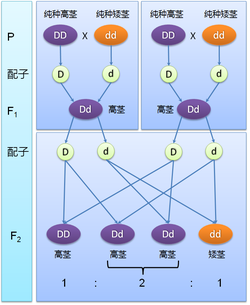
孟德尔在他有划时代意义的论文当中，运用自己建立的遗传学分析方法，研究豌豆的不同性状，确定了两种重要的实验现象：第一，生物的性状由颗粒性遗传因子决定，不是由外界环境条件所决定。双亲把遗传因子传递给下一代，不是直接把性状传递给子代。第二，具有显性性状同具有隐性性状的两亲本进行杂交的结果，隐性性状并没有消失，仍然保存在杂种个体和杂种后代中。所谓颗粒遗传，就是与融合遗传相对，认为遗传因子是一份一份的，不会因为在代际传递而产生或消失。遗传学家拉巴少夫在其《遗传学》教科书里强调这两条原则对进化论有着极为重要的意义，因为它揭示了变异的主要来源和物种的适应性状能够屡代保存的内在机理。随着30多年后孟德尔定律的重新发现和证实，这些原则不但彻底否定了希波克拉底以来流传的泛生说，推翻了后天获得性状可以遗传的理论，而且驳倒了融合遗传学说，并因此使詹金提出的融合淹没学说失去了意义。

孟德尔遗传学范式的提出是基于特定的历史背景。第一，孟德尔运用了大规模实验来探究生命体遗传规律。由于实验科学的建立，人们相信通过实验手段可以模拟自然界中存在的情况，并且逐渐产生了设计实验、控制变量来探究世界运行规律的方法。第二，孟德尔还是第一位在生命科学中引入了数学的科学家。原先，在生命科学领域中，人们主要通过观察来建立规律。然而孟德尔是一位受过数学教育的修道士，这一事实表明在孟德尔的时代，数学教育成为了高等教育的重要部分，也反映了数学在当时历史条件下的地位。孟德尔的数学背景无疑对他在生物学中创造性地引入统计工具起到了重要作用，而这是因为当时社会上存在的数学化潮流。第三，孟德尔提出的颗粒遗传观念是一个数学化的模型，在当时并无对应的物理实在。这一方面是因为他扎实的数学功底，另一方面，考虑到孟德尔曾经多年教授物理学实验，这一理论的提出也可能受到了原子论的影响。道尔顿原子论的物理实在同样无法证明，但通过气体化学现象可以建立起原子模型。

孟德尔遗传学范式的建立不仅是遗传学的第一个范式，其颗粒遗传理念还直接影响了经典遗传学的建立。

经典遗传学

经典遗传学和范畴论

正是自孟德尔之后，遗传学渐渐可被范畴论描述了。一个范畴（Category）是一个简单得令人尴尬的概念。一个范畴完全由物体和箭头组成一个对象可以画为一个圆或者一个点，一个箭头，就是一个箭头。但是,范畴的本质是构成。或者说构成（Composition）的本质是范畴。箭头相互组成，如果你有一个箭头从物体A到物体B，另一个箭头从物体B到物体C，那么一定有一个箭头-它们的组成-从这里开始A到C。

从孟德尔遗传学到经典遗传学，介于常规科学与范式转变之间。一方面，孟德尔遗传学中的遗传因子概念被完整地继承了，经典遗传学只是揭示了遗传因子本身的性质和它们之间的关系。可以说，孟德尔遗传学与经典遗传学有相似的理论基础。另一方面，经典遗传学时代的“科学共同体“对遗传因子本质的认识与孟德尔完全不同。孟德尔提出的遗传因子是唯象的，即类似于一个模型，而经典遗传学谈论的遗传因子是以染色体作为载体，因此其基础又有所不同。基于后一点原因，笔者将孟德尔遗传到经典遗传学的转变归为一次范式转变。在经典遗传学范式下，涌现出了一大批遗传学发现，比如红绿色盲的伴性遗传，也同样存在像转座子理论这类的反常发现。

经典遗传学范式是建立在对基因的理解之上的。尽管这种理解不是绝对的，尤其是在范式建立初期它容许一定的模糊性存在，但它是必要的，因为在某种共同观念形成之前，常规科学是无法广泛展开的。而经典遗传学范式对于基因的理解有三大基础，一是基于孟德尔分离和自由组合定律，基因是不可融合的在遗传时彼此分离的遗传粒子，二是杂交实验和对细胞中染色体行为的观察所暗示的，基因在染色体上线性排列，三是在果蝇诱变实验后所提出的，基因是突变的功能单元。

孟德尔遗传的再发现对遗传因子概念的继承起了决定性作用。英国遗传学家贝特森（W. Bateson, 1861-1926）在1897年对家鸡的冠形和羽色进行杂交实验，发现了与孟德尔类似的分离比率。1899年7月11日，在英国伦敦召开的第1节国际遗传学大会上，贝特森提出了应当注重研究生物单个性状的遗传规律。而在此次大会后的第二年，德弗里斯、科伦斯、丘歇马克通过各自独立的植物杂交实验，重现了孟德尔1866年的论文“植物杂交试验“中的分离定律。科学史上把这一重大事件定义为孟德尔定律的重新发现，为经典遗传学的建立奠定了重要基础。“基因成对存在，在遗传过程中彼此分离”，成为经典遗传学对基因性质的基本理解之一，并且使基因的行为以及关系成为经典遗传学研究的核心。

而摩尔根关于果蝇的一系列杂交实验，发现了基因的连锁遗传规律，并且他们结合对染色体行为的观察以及实验验证，认为基因存在于染色体上，并且是线性排列的，位于同一条染色体上的基因在遗传时通常不会彼此分离，除非发生了同源染色体的重组交换。而同源染色体重组发生的频率与基因之间的距离有关，因此可以通过统计后代中重组型配子的比例计算基因之间的相对距离，并且进一步绘制生物的遗传学图谱。摩尔根实验室的一系列工作使得经典遗传学的范式真正建立。

后来摩尔根的学生米勒，报告了X射线诱导果蝇基因突变的发现，认为基因是可以发生突变的结构单元。它既建立了染色体上基因的改变与生物性状的改变之间更加直接的关联，又佐证了正向遗传学策略的合理性，即每一种不同的性状由其对应的基因负责产生，故可以对相应的基因进行定位。“基因是突变的结构单元”这一观念，完善了经典遗传学范式对于基因功能的理解，同时X射线诱变手段使经典遗传学的研究方法得到进一步拓展。

经典遗传学范式的核心是染色体上的基因控制性状，这个范式具有可以观察到的物质基础，以及实验可验证的发生机制，大大降低了遗传过程的神秘性以及不可预测性。相比于融合遗传、范生论等其他范式，它的优越性显而易见，于是它深刻影响了时代对于遗传和进化的观念。在二战时期，经典遗传学理论也应发了基因决定论的出现，进而被广泛用于为种族灭绝政策背书。这提醒我们需要警惕对科学理论的不合理外延，以及那些以科学之名服务于个人或团体利益的行为。

在经典遗传学的范式下，常规科学广泛开展，而库恩所说的反常也的确出现了。美国的遗传学家芭芭拉·麦克林托克（Barbara McClintock，1902－1992）在1951年提出了转座子模型，认为基因可以在染色体上跳跃，这与经典遗传学认为的基因在染色体上固定不动、线性排列有本质的冲突。尽管她精湛地运用了经典遗传学的范式，她的结论却动摇了该范式下“科学共同体”的共同信念，于是她的假说在经典遗传学范式统治的数十年间一直不被认可。而也是在分子遗传学范式建立多年之后，她的发现才终于在新的范式下被成功解释。然而，库恩认为，常规科学的反常现象愈发严重的时候，就会引发危机，爆发科学革命，带来范式的转变。但我们发现，尽管反常总是出现，但是它对于新范式的形成并不是必要的。因为分子遗传学范式的建立就不是为了解决反常问题或者危机，而是基于科学家对DNA双螺旋结构的新发现。即使“科学共同体”预见到它将能够回答更多问题，它在建立之初对于经典遗传学范式中留下的反常问题往往也是无法解决的。

香农和遗传学

信息和信息熵

信息是物质、能量、信息及其属性的标示。【维纳对信息定义】

信息是确定性的增加。【香农(Shannon)信息定义】

信息是事物现象及其属性标识的集合。【现代普遍接受的定义】

信息理论的鼻祖之一Shannon把信息（熵）定义为离散随机事件的出现概率。 所谓信息熵，是一个数学上颇为抽象的概念，在这里不妨把信息熵理解成某种特定信息的出现概率。而信息熵和热力学熵是紧密相关的。根据Charles H. Bennett对Maxwell's Demon的重新解释，对信息的销毁是一个不可逆过程，所以销毁信息是符合热力学第二定律的。而产生信息，则是为系统引入负（热力学）熵的过程。所以信息熵的符号与热力学熵应该是相反的。 一般而言，当一种信息出现概率更高的时候，表明它被传播得更广泛，或者说，被引用的程度更高。我们可以认为，从信息传播的角度来看，信息熵可以表示信息的价值。这样子我们就有一个衡量信息价值高低的标准，可以做出关于知识流通问题的更多推论。

熵又称为自信息(self-information),表示信源 X 每发一个符号(不论发什么符号)所提供的平均信息量。自信息的概念可以与下文提到的互信息相参照。

Shannon提出的信息熵公式：计算公式为：

H(x) = E[I(xi)] = E[ log(1/P(xi)) ] = -∑P(xi)log(P(xi)) (i=1,2,..n)

其中，x表示随机变量，与之相对应的是所有可能输出的集合，定义为符号集,随机变量的输出用x表示。P(x)表示输出概率函数。变量的不确定性越大，熵也就越大，把它搞清楚所需要的信息量也就越大。从定义式,我们可以看出,虽然信息熵经常被称为负熵,但是其取值恒为正,这是因为pi恒小于1。不过，由于信息的接受就是不肯定性的消除，即熵的消除（此处的熵取“热力学熵”中“熵”的含义），所以信息熵才常被人称作负熵。熵的取值范围为[0~lgK]。

为什么信息熵和遗传学有关？

信息熵是离散随机事件的出现概率。而基因分离，基因重组这两个遗传学中的基本问题都可以用随机事件来表达。

香农研究的群体遗传学

香农研究的遗传学被称作群体遗传学，其中的重要概念如下：

1. 群体遗传学研究对象是群体，它是能互交繁殖的个体集合，又称为孟德尔群体
2. 基因库：群体中所有个体在所研究的同一性状中共有的全部基因
3. 孟德尔群体基因库中的各个基因使用基因频率表示的，各个基因型使用相应的基因型频率表示的
4. 孟德尔群体的遗传结构：它的基因分布和基因型分布
5. 群体遗传学中主要研究的是质量性状，数量表达通常用具有有限个状态（值）的离散型随机变量实现

为避免误解，我将重要的对应关系澄清如下：

1. 生物进化单元——孟德尔群体——宏观系统
2. 遗传结构——基因状态和基因型状态的分布——状态分布
3. 种内进化——群体遗传结构在一些影响因素下世代间发生的变化——熵

群体遗传学是群体中的基因随世代而变化的动力学，从分子进化来讲，它应是核苷酸随时间突变的动力学

群体遗传学的发展历程

群体遗传学最早起源于英国数学家哈迪和德国医学家温伯格于1908年提出的遗传平衡定律。以后，英国数学家费希尔、遗传学家霍尔丹(Haldane JBS)和美国遗传学家赖特(Wright S)等建立了群体遗传学的数学基础及相关计算方法，从而初步形成了群体遗传学理论体系，群体遗传学也逐步发展成为一门独立的学科。群体遗传学是研究生物群体的遗传结构和遗传结构变化规律的科学，它应用数学和统计学的原理和方法研究生物群体中基因频率和基因型频率的变化，以及影响这些变化的环境选择效应、遗传突变作用、迁移及遗传漂变等因素与遗传结构的关系，由此来探讨生物进化的机制并为育种工作提供理论基础。从某种意义上来说， 生物进化就是群体遗传结构持续变化和演变的过程， 因此群体遗传学理论在生物进化机制特别是种内进化机制的研究中有着重要作用。

在20世纪60年代以前，群体遗传学主要还只涉及到群体遗传结构短期的变化，这是由于人们的寿命与进化时间相比极为短暂，以至于没有办法探测经过长期进化后群体遗传的遗传变化或者基因的进化变异，只好简单地用短期变化的延续来推测长期进化的过程。而利用大分子序列特别是DNA序列变异来进行群体遗传学研究后，人们可以从数量上精确地推知群体的进化演变， 并可检验以往关于长期进化或遗传系统稳定性推论的可靠程度。同时， 对生物群体中同源大分子序列变异式样的研究也使人们开始重新审视达尔文的以“自然选择”为核心的生物进化学说。20世纪60年代末、70年代初，Kimura、King和Jukes相继提出了中性突变的随机漂变学说: 认为多数大分子的进化变异是选择性中性突变随机固定的结果。此后，分子进化的中性学说得到进一步完善，如Ohno关于复制在进化中的作用假说: 认为进化的发生主要是重复基因获得了新的功能，自然选择只不过是保持基因原有功能的机制；Britten甚至推断几乎所有的人类基因都来自于古老的复制事件。尽管中性学说也存在理论和实验方法的缺陷， 但是它为分子进化的非中性检测提供了必要的理论基础。“选择学说”和“中性进化学说”仍然是分子群体遗传学界讨论的焦点。

这样的群体遗传学是否具备可计算性？

借用杨濠旗同学在他的结题作业中对知识的可计算性的精辟总结。一个知识体系能否在有限的时间内被归并和表达本质上取决于知识的可计算性，亦即一个运算程序能否在有限的时间内终止。我们需要使用抽象表达（abstract interpretation）的方式进行信息压缩，将实际问题中无限维空间内变动的信息压缩为一组有限的方程，进而通过有限次的判断了解程序运行的实际进度。这与Galois使用群论解决高次方程的可解性问题有异曲同工之妙，我们在命名空间（namespace）中使用度量、估测、塑形、加密、聚类等方式实现信息的压缩。知识的可计算性在现实中的应用就是顾老师所学习和研究的系统工程领域，在复杂工程中我们需要一套组织多层次关系的自洽计算方法来客观标识不同子系统的相互作用。让这套计算方法达到尽善尽美的层次是不现实的，亦即“巴别塔的魔咒”，群体遗传学需要在泛用性和精确性、侧重关系和侧重结构这两种矛盾关系之间做一定的取舍。通过在模型空间中进行反复迭代的模型搜索，最终可以形成一套自动化系统设计的产业化工具。

基因型熵作为群体混杂度的一种普遍性测度

群体的熵是对群体混杂程度的一种描述．熵所意味的杂，指混乱 (confused，mixed，disarranged，assorted，untidy，mess)或无序(disorderly，out of order)而杂种优势的杂，是指异质性 (heterogeneity)，是杂合子本身基 因的异质性所 引起 的 ，并非杂合子与纯合子混 在一起造成的群体混杂(后者才是熵所描述的混杂)．由于随机交配 (混交 )而达到 Hardy—Wehaberg平衡的混杂群 的熵最 大 (这 可以与达 到热 平衡的 ，热力学体 系的物理熵最大相 类比)，而纯系 的熵最小．混交 、迁移与融合均会导致 尚未平衡的群体增 加混杂 程度 ，即增加熵 (基因型熵 )这是 群体遗传学中的“熵不减少定律 ，可以与热力学 第二定律相类 比．群 体遗传学中的这一定律可 以表示为 △ H= H-H0。式 中△H 表示 混交 、迁 移或融合之后群体 的熵 (基因型 熵)与此前 的熵 值之差．只有 当群体 已 达平衡或各亚群体 中基因频率都相等时 ，才有△H=0． 至于 杂交 ，却并 不导致群 体的熵增 加．例如选 择不 同性 别的一群 自 鼠和一群 黑 鼠进行杂交 ．则杂交 子一代 中仅有均 匀一致的 杂合子 ，从基因型来说 ，杂 交子一代 的群体是 纯 的．与纯种群 体一样 ，基因塑熵最小 (这是表现 杂种 优势的前提之一)．子一代群体 混交后 ，子二代 即达 平衡 ，熵值增加 ，杂种优势 也随之消失．如果 一群 自鼠与一群黑 鼠，两群 中雌雄个体都有 ，把它 们置于一处 ，所进行的就是混交 (随机交 配 )而不是 杂交．只 需一代 即可达到平 衡 ，熵值 (基 因型熵 )增至最 大 ，不 可能 出现杂种 优势。 作为群体混杂度的一种普遍性描述或测度，基因型熵是合适的．无论群体是否 已经达到 Hardy—Weinberg平衡，这一测度均可适用．对于尚未达到平衡的群体 ，这时基因型频率与基因 频率之间没有一定的函数关系，则可从基因型频率本身来直接定义基因型熵．则不适用于未平衡的杂交子一代群体．这时群体的基因熵达到最大值，而群体 的混杂度最小．至于表型熵，由于显性的影响．掩盖了AA和Az型合子的混杂性，已经不再是单纯的凸函数t更不适合于作为 群体混杂度的测度．

以下将澄清几个下文将常常出现的概念：

群体（Polulation）：是指生活在一定空间范围内，能够相互交配并生育具有正常生殖能力后代的同种个体群。

等位基因频率（Alleles frequency）：在一个群体中，某类等位基因占该基因位点上全部等位基因数的比率。

基因型频率（Genotype Frequence）：群体中某一基因型个体的数目占群体总个数的比例。可以反映某一基因型个体在群体中的相对数量。

遗传平衡定律或哈迪.温伯格定律（Hardy-Weinburg）：在随机交配下的孟德尔群体中，如没有替他因素（基因突变、迁移和选择）的干扰，群体的基因频率和基因型频率将逐代保持不变。

连锁平衡（Linkage equilibrium）：两个基因座的等位基因组合的频率等于组成组合的等位基因各自频率的乘积，不存在优势组合，称为连锁平衡。

连锁不平衡（Linkage Disequilibrium）：相邻位点之间的非随机关联，当一个位点上的某一等位基因与另一位点上的等位基因共同出现的概率大于随机组合的假设，则这两个位点之间存在连锁不平衡。

适合度（fitness）：指一个个体能够生存并将其基因传给下一代的能力，可用相同环境中不同个体的相对生育率来衡量（即在选择中，某一基因型个体在下一代平均保留后代数的比率）。

选择系数或淘汰率（selectivity coefficient，用s表示）：某一基因型个体在下一代淘汰的个体数占总后代数的比率。

群体分层（population stratification）：群体分层是指群体内存在亚群的现象，亚群内部个体间的相互关系大于整个群体内部个体间的平均亲缘关系。

核苷酸多态性(π)：衡量特定群体多态性高低的参数，是指在同一群体中随机挑选的两条DNA序列在各个核苷酸位点上核苷酸差异的均值。π值越大，说明其对应的亚群多态性越高。

热力学中的熵和遗传学中的熵的相似之处

无论是统计物理学中Bohzmann关系式定义的熵(S=klnW)，还是信息论中Shannon公 式定义的熵都具有以下性质：(1)熵是一个与体系中各元素的概率有关的一个函数 I(2)体系中各元素的概率值相等时，熵值最大，(3)熵是对于概率的凸函数，(4)体系的融合不可能使熵减少，而往往使熵增加。

Mutual Information

互信息（Mutual Information）是信息论里一种有用的信息度量，它可以看成是一个随机变量中包含的关于另一个随机变量的信息量，或者说是一个随机变量由于已知另一个随机变量而减少的不肯定性，互信息具备对称性和半正定性。信息论奠基人香农（Shannon）认为“信息是用来消除随机不确定性的东西”，也就是说衡量信息量的大小就是看这个信息消除不确定性的程度。 实际上，信息是一个不能被定义的“元概念”。香农说：“‘信息’这个词在信息论的一般领域已经由各位作者赋予不同的意义。至少，这些意义很可能在某些应用领域充分证明是有用的，需要进一步的研究和做出永久性的承认。几乎不能指望一个单一的关于信息的概念能够令人满意地对一般领域的各种应用负责。”

简单地说，互信息就是知道X，给Y的信息量带来多少损失（或者知道Y，给X的信息量带来多少损失）。

香农用信息编码遗传学的意义

当信息可以度量，意味着几乎所有事物都能够用数据测量和编码，因为归根结底，一切都与信息脱不开关系。传统意义上的函数描述从对想到对象，抽象的函子可以有2、3、4、5、6等等抽象层，可以比较对象本身也可以比较对象的关系，这样的策略是具有万用性的，可以规模化，产业化，自动化。

香农和图灵二人都使用编码，图灵是将指令编码变成数，将十进制数编码成0和1，而香农是对基因、染色体、继电器和开关编码。香农的博士论文题目就是《理论遗传学的代数学(An Algebra for Theoretical Genetics)》。很多人不知道这篇论文写的是什么，都只是从题目上扫那么一眼，认为就是用数学方法研究人类遗传学的。其实这篇文章的直到今天都没有引起注意，一个原因是该文直到1993年才被正式发表。另一个原因恐怕与他当年的《通信的数学理论》一样，工程师认为数学太深，数学家没有工程学背景。同样，现在这篇论文也是，遗传学家看不懂，数学家不去看的论文。

尽管这篇论文处于舅舅不疼，姥姥不爱的尴尬处境，但它真正将理论遗传学的代数学建立起了联系。正如IBM公司的数学家蔡汀（G. Chatin）不久前撰写了一本《证明达尔文：进化和生物创造性的一个数学理论》（Proving Darwin：Making Biology Mathematical）的书。他就是希望用数学的方法证明达尔文的进化论，试图揭示生物学深层的数学结构，开辟了一个称之为“元生物学”的新领域。香农的博士论文会不会是未来遗传学研究的一个崭新方向呢？

香农早已经注意到电路与布尔代数之间的类似性，即把布尔代数的“真”与“假”和电路系统的“开”与“关”对应起来，并用1和0表示。而在他的博士论文《理论遗传学的代数学》中，他构造了一个用于研究孟德尔种群动力学的代数。代数符号代表个体或种群的群体。例如，索引符号'h j i k'表示一个考虑两个基因位点的群体(位点的数量对应于索引对的数量)。每个位点的等位基因型数完全是任意的，位点的重组值也是任意的。一个种群符号的不同组成部分，通过将指数固定在特定的值来表示，这些数字的值对应于具有一定遗传公式的种群的分数。在某些情况下，将其分量为负甚至复杂的总体符号考虑为方便。当然，这些符号不能代表一个实际的个体群体，被称为不可实现的群体，但它们的使用有时有助于解决问题。

两个总体符号R=h j i k + S=h j k,导致三分之一人口的象征就是以这样一种方式定义为代表的人口仅仅通过结合相对应的原始分数比例人口标量人口系数R和s .交叉乘法符号*给出了一个种群符号，其定义方式是当两个原始种群随机交叉时，表示期望的后代种群。当考虑两个基因座时，这是通过数学定义h j i k *h j I k 的交叉乘法，其中p1 = 1 - p0为两个位点的重组值，用点替换一个索引表示该索引上的总体符号的和。交叉乘法的定义类似于n个位点。证明了该代数在加法和乘法上是交换的，在加法上是分配律，在加法上是结合律，而在乘法上不是。这些定律和两个基本的操作定理构成了代数的基本算法:一是总体上所有指标的总和是统一的，二是总体上指标的上下行倒转保持不变。

许多著名的理论遗传学定理都很容易用这个代数来证明。此外，还发现了一些新的结果。在任意初始种群随机互交的情况下，分别推导了2个和3个相关因子情况下第n代子代的完全通式。以及对于两个相关联的因子，第n代的公式。与此同时，还表明了一个重组值在当没有干扰时，1/2是不可能的。在考虑一个或多个基因座的情况下，找到了种群在随机交配条件下的稳定性。对于一个轨迹的情况，建立了三组等价的充要条件。

通过某种齐次函数?种群:任意的种群可以扩展成一个有限的级数，显示它的各个组成部分。这个展开式，连同交叉乘法*，将这个代数的元素显示为超复数。证明了任意种群可以被唯一地扩展为任意n个线性独立种群的和，其中n为考虑因素的不同可能遗传公式的个数。

利用加法和交叉乘法的运算，可以写出涉及已知和未知总体的各种类型的方程。一般来说，这样一个方程可以解释为一个涉及一个或多个未知群体的育种实验，结果是一个遗传上已知的群体。在有解的情况下，大多数这样的方程都可以得到求解。简单地说，这种解法可以概括如下。通过对未知种群的一个或多个指标进行求和，得到了关于未知种群的足够数据，从而唯一地确定它们所出现的任何叉积。原始方程中的叉积项就可以已知，方程可以用与普通线性代数方程完全相同的方法求解。

如果存在有利于具有某种遗传结构的个体的选择行为，那么先前的稳定性公式就不再成立。虽然这个更困难的问题还没有完全解决，但它建立了在任意给定的选择作用下可能存在稳定种群的必要条件，并给出了这个种群的公式。

香农开始了种群演算的发展，即对可能随时间而不断变化的种群的研究。定义总体的时间导数。种群的导数虽然是一个索引符号，但它本身不是种群。所有普通的求导规则，包括对总体叉积求导的莱布尼茨规则，都被证明是正确的。此外，种群可以按时间幂级数展开为泰勒级数，其形式与普通泰勒级数相同。

重要结论

1. 哈温伯格平衡定理，平衡群体shannon信息熵最大
2. 固定有利基因的过程是熵减过程
3. 核苷酸突变和相邻位点突变具有保墒性质，表明DNA是封闭系统

熵变规律是生物进化的本质。只有开放系统才能使有利基因增加，这种有利基因频率增加的过程是产生负熵的过程，亦是生物向环境索取生存物质和空间的过程。

现代遗传学

遗传学第三次范式转变始于DNA双螺旋结构的发现。尽管因为双螺旋结构深入人心、广为人知，DNA结构本身受到更多关注，但这项工作的另一项重要意义是确认了DNA的复制模型；为之后科学家们研究半保留复制，探索遗传物质发挥作用的方式，提出中心法则，并开辟反式遗传学等一系列工作埋下了伏笔。DNA双螺旋结构的发现，标志着人类对遗传物质本身及其作用机制的研究具体到了原子、分子层面。基于这些发现，分子生物学技术能更精细地描述基因的性质；生物化学能结合遗传学阐明各生物分子的作用机制。遗传学、分子生物学、生物化学三个现代生物学的重要分支，通过这一发现被结合在一起，形成了新的研究范式。

1953年沃森（J.D.Watson）和克里克（F.H.C.Crick）发表了DNA的双螺旋结构。DNA既然是主要的遗传物质，它必须具备自我复制的能力，即通过复制形成新的和原来一样的DNA分子的能力。但双链DNA是如何解链、如何进行复制和如何保证DNA序列不变的，一直有很多的假说，如全保留复制和全保留复制等。

1958年美国科学家马修·梅塞森（Matthew Meselson）和富兰克林·斯塔尔（Franklin Stahl ）的DNA同位素标记试验证实了DNA的双螺旋结构和半保留复制机制。DNA分子独特的双螺旋结构，为复制提供了精确的模板，通过碱基互补配对，保证了复制能够准确地进行。这一发现成功地解释了生物遗传的连续性和稳定性。

1957年9月，克里克提交给实验生物学会一篇题为“论蛋白质合成”的论文。这篇论文被评价为“遗传学领域最有启发性、思想最解放的论著之一”。在这篇论文中，克里克正式提出遗传信息流的传递方向是DNA→RNA→蛋白质，后来被学者们称为“中心法则”。其中DNA记录着生物信息，RNA传递生物信息，最终合成出蛋白质。蛋白质作为生物体内的分子机器，维持着生命的运转。这意味着人类开始从分子层面认识遗传信息的储存和发挥作用的方式。

从偏序集看中心法则

偏序仅仅是在集合X上的二元关系≤(这只是个抽象符号，不是“小于或等于”)，它满足自反性、反对称性和传递性。即，对于X中的任意元素a,b和c，有:

'自反性：a≤a;'
'反对称性：如果a≤b且b≤a，则有a=b;'
'传递性：如果a≤b且b≤c，则a≤c 。'

带有偏序关系的集合称为偏序集。

因此，我首先粗略的定义集合为{DNA RNA Protein}。如果我们定义：一个反链A是X的一个子集，如果A的任意两个元素都不能进行比较。一个链C是X的一个子集，如果C的任意两个元素都可比。那么，在逆转录病毒发现之前，该偏序集只有链而无反链，所有生物的遗传信息的偏序关系是一定的，即：DNA≤RNA≤Protein。这里的‘≤’代表了遗传信息的传递的方向，这样一条链代表了遗传信息的传递是不可逆的。根据自反性，DNA≤DNA代表DNA的复制，RNA≤RNA代表RNA的复制。

但是，逆转录病毒的发现打破了这样的偏序关系。出现了RNA≤DNA≤RNA≤Protein这样一条链，而这种闭环结构的出现使得这个集合不再是一个偏序集。于是旧的中心法则面临挑战，新的范式将应运而生。但即使有了回圈，新的遗传信息传递过程依然可以被偏序集表达。

应运而生的新范式

1965年，科学家发现RNA可复制；1970年，科学家发现逆转录酶；1982年，科学家发现疯牛病是由一种结构异常的蛋白质引起的疾病。中心法则日益完善，最终成为现代生物学中最重要最基本的规律之一。中心法则在探索生命现象的本质及普遍规律方面起了巨大的作用，极大地推动了现代遗传学的发展，是现代遗传学的理论基石，并为生物学基础理论的统一指明了方向，在生物科学发展过程中占有重要地位。如果说1953年DNA的双螺旋结构的发现拉开了科学革命的序幕，那么1957年“中心法则”的提出则意味着新范式依然建立，标志着遗传学的发展进入到在“中心法则”范式指导下的常规科学发展阶段。

科学革命刚结束不久，研究理论如雨后春笋涌现。经典遗传学的认知路线为由表及里，即通过杂交等手段观察表型性状的变化而推知遗传基因的存在与变化。但随着分子遗传学及相关实验技术的发展，科学家已经能够在分子水平上进行操作，有目的地对DNA进行重组或者定点突变。因此，现代遗传学中就出现了另一条由里及表的认知路线，即通过DNA重组等技术有目的地、精确定位地改造基因的精细结构以确定这些变化对表型性状的直接影响。由于这一认知路线与经典遗传学刚好相反，故将这个新的领域作为遗传学的一个分支学科，称为反向遗传学。

深入分子层面的研究还引发了对沉寂已久的表观遗传的再讨论。早在1942 年的时候,C. H.Waddington 就首次提出了表观遗传一词,并指出表观遗传与遗传是相对的,主要研究基因型和表型的关系。但因为他的理论与孟德尔的经典遗传学尖锐对立而被人们忽视。直到1984年，霍利迪(R. Holiday) 针对表观遗传提出了更新的系统性论断,也就是人们现在比较统一的认识,即表观遗传学研究没有DNA 序列变化的、可遗传的基因表达改变。

技术的改良打破了学科间的壁垒，学科间的“不可通约性”减弱了，遗传学、分子生物学、生物化学三个现代生物学的重要分支交叉发展趋势日益明显。

于1990年正式启动的人类基因组计划就是其中的典型代表。通过生物化学的部分酶解法，分子生物学的凝胶色谱法，美国、英国、法国、德国、日本和中国科学家共同参与了这一预算达30亿美元的人类基因组计划。这一计划把人体内约2.5万个基因的密码全部解开，同时绘制出人类基因的图谱，揭开组成人体2.5万个基因的30亿个碱基对的秘密。21世纪以来，得益于分子生物学的发展，一项基于古细菌特异性免疫的基因编辑方法——CRISPR快速发展，编辑速度远远超越锌指核酸酶和其他编辑工具。CRISPR打开未来基因编辑应用的大门，也是遗传学在稳健发展的常规科学阶段的典型成果。

从范式转换看拉马克主义的兴衰

科学进步是螺旋型地上升，在某个维度上，新范式可能与某个久远的旧范式有共通之处。拉马克主义学说一度被孟德尔学说的后继者抛弃，但表观遗传学的诞生让拉马克主义有了重回神坛的机会。

沃森和克里克的贡献

双螺旋结构是一个包含迭代（iteration）和分支（Branch）的简单结构!(迭代与时间有关，分支与空间有关)，这大大增强了遗传学的可表达性。事实上，结构的复杂性确定更新的时钟速度。

遗传学的新重点

现代遗传学的心中点有如下这些：

群体间固定指数(Fst)：衡量群体中等位基因频率是否偏离遗传平衡论比例的指标，用来研究不同群体间的分化程度。其取值为0到1，0代表两个群体未分化，其成员间是完全随机交配的；1代表两个群体完全分化，形成物种隔离，且无共同的多样性存在。

θw：Watterson’s 多态性估值，从理论上说，在中性条件下，应当有θW=4Neμ的平衡状态，Ne表示有效群体大小，μ表示每一代的序列突变率。

瓶颈效应（Bottle effects）：由于环境骤变(如火灾、地震、洪水等)或人类活动(如人工选择、驯化)，使得某一生物种群的规模迅速减少，仅有一少部分个体能够顺利通过瓶颈事件，在之后的恢复期内产生大量后代。

基因的随机漂移或遗传漂变（random genetic drift）：由某一代基因库中抽样形成下一代个体的配子时发生机误，这种机误引起基因频率的变化称之为基因的随机漂移或遗传漂变。换句话说，就是利用随机抽样的办法建立小群体时，由于抽样误差引起基因频率随机波动的现象。

始祖效应、奠基者效应或建立者效应（Founder Effect）：有少数个体的基因频率决定了他们后代中的基因频率的效应，是一种极端的遗传漂变作用。

迁移压力(又叫基因流,Gene Flow)： 由于某种原因，具有某一基因频率的群体的一部分移入基因频率与其不同的另一群体，并杂交定居，就会引起迁入群体的基因频率发生改变。

有效群体大小（effective population size，Ne）： 是指与实际群体具有相同基因频率方差或相同杂合度衰减率的理想群体大小,它反映了群体平均近交系数增量的大小以及群体遗传结构中基因的平均纯合度。

中性学说（neutral theory）： 认为分子水平上的大多数突变是中性或近中性的，自然选择对它们不起作用，这些突变靠一代又一代的随机漂变而被保存或趋于消失，从而形成分子水平上的进化性变化或种内变异。

突变压力：一定条件下，一个群体的突变率可明显增高，形成突变压力，使某个基因频率增高。 选择压力（selection pressure）：受某种环境条件的影响，某些突变型被选择所作用，使突变基因的频率降低。

选择（selection）:在人类和自然界的干预下，某一群体的基因在世代传递过程中，某种基因型个体的比例所发生变化的群体遗传学现象。

陈哲睿的偏序结构对我的启发

陈哲睿将流行病学现场调研的开展顺序进行了一定的排序。我将使用偏序结构的方法，对于他们靠直觉和经验总结出来的调查步骤和方法进行抽象，形成一个具有偏序结构的完整的拓扑空间。从而能够更好的将相应的调查方法进行推广。偏序集合在数学中指的是具备了某种偏序关系的集合。偏序集合将对于集合的元素进行排序、顺序或者排列等直觉概念抽象化。在抽象化排序观念后形成的具有偏序结构的拓扑空间，这种空间也叫做偏序空间。

借用陈哲睿同学在他的结题作业所表达的灵感，我可以对遗传信息的表达进行排序：DNA≤RNA≤Protein。用两个‘≤’表达“转录”和“翻译”两个阶段：

具体来讲：转录:是在细胞核中进行的，是指以有遗传效应的DNA分子片段中的一条链为模板合成RNA的过程。通过转录，DNA分子就把遗传信息传递到RNA上，这种RNA叫信使RNA,简称mRNA。翻译:是指以信使RNA为模板，合成具有一定氨基酸顺序的蛋白质的过程，是在细胞质的核糖体.上进行的，与此同时需要转运RNA的协助。 信使RNA合成后，通过细胞核的核孔进入到细胞质，与核糖体结合。转运RNA按照信使RNA的密码子顺序，运载着特定的氨基酸到核糖体上。核糖体将接受的氨基酸经过缩合形成肽键，使肽链不断延长。当核糖体遇到信使RNA的终止密码子时，肽链的合成终止。肽链离开核糖体，经过折叠形成具有一定空间结构的蛋白质分子。由此可以看出，通过转录和翻译过程，DNA分子，上的遗传信息转移到蛋白质上，实现了基因对性状的控制。中心法则指遗传信息在细胞内生物大分子之间传递的全过程。这是由美国的科学家F.H. C克里克在1957年提出的，当时的研究表明，遗传信息在不同的生物大分子间的转移都是单向的，可用这样的关系式表示: DNA- +RNA- +蛋白质;后来，有人发现一些RNA病毒在其宿主细胞中的复制是先以病毒的RNA分子为模板合成一个DNA分子，然后再以DNA分子为模板合成新的病毒RNA。于是，克里克于1970年在重申中心法则的重要性的同时，对中心法则做了相应的修改。遗传信息的传递途径有5条。1.DNA自我复制，遗传信息从亲代细胞传递给子代细胞。2.通过转录，遗传信息从DNA传递给信使RNA。3. 通过翻译，遗传信息从信使RNA传递给蛋白质分子。4.通过逆转录，遗传信息从RNA传递给DNA。5. RNA能够自我复制，遗传信息从亲代传递给子代。中心法则的提出，不仅阐明了生物体遗传信息的传递规律，为进一步探讨生物大分子之间的关系指明了方向，也为基因工程等生物技术提供了指导。

由于以上的过程是满足反自反性的，所以这是一个严格偏序集。

结语

在遗传学的发展过程中，发生了三次范式转变。第一次是颗粒性遗传因子的提出，第二次是对遗传因子在光学显微层面的认识和对其排列方式的认识，第三次是在分子层面上认识。其中每一次范式转变都会引入大量新的研究手段和新的问题，这无疑符合库恩对范式转变的定义。然而，笔者也注意到，遗传学的三次范式转变都存在在尺度上向微观发展的趋势，这一趋势无疑来自于其他学科。

遗传学的范式转换来自命名空间中“量子”单位的缩小（或者度量衡的改变）和对刻画中心法则的偏序集的修正。前者也是信息熵所测度的对象的改变，后者也是遗传信息流动箭头的改变。

课程感悟

第二周：

 key-value pair 揭示了复杂网络系统工作原理的本质。用这样的方式去理解范式转换，就会发现科学革命实际就是key-value pair 的扩增与删减；不可通约性来自命名空间的不同。而这样的不可通约正是历代科学家致力于消除的，这就像科学家们企图寻找科学语言的“罗塞塔石碑”一样。以人工智能为例：微软近期就提出了深度学习框架的通用语言——repo1.0，他们希望通过构建这一深度学习框架“罗塞塔石碑”，让研究者们能够在不同框架之间轻松运用专业知识，并且实现不同开源社区之间的合作。如果这能实现，就可以创建一个跨语言对比的常用设置（Python、Julia、R），实现不同开源社区之间的合作。
 另外，我个人认为key-value pair也并非全无缺陷。尽管key-value式的查询方法有查询速度快、存放数据量大、支持高并发等等优点，但缺点也是显著的，那就是不能进行复杂的条件查询。甚至当这样的pair数量累计到了一定层次后，key本身的搜寻都极为不易，原本的key也变成了value，需要找到更高一阶的key与之对应才能解决这一问题。

第三周：

 课上的视频让我想到Paul Nurse的一句话：生命的深层结构指的是细胞或有机体这样的基本单元，它们能够自我繁殖，并允许微小的变异。繁殖与变异共同通过自然选择推动物种的演化，从而形成多样化的生物种群。它们不仅能够在变化的环境中存活，还能够利用新的机会。而那些成功适应环境的单元就能继续繁殖后代。
 类似的机制在不同的尺度上都发挥着作用，构成了众多关键生物过程的基础。一个复杂系统会有一些很小的东西组成，由这些很小的东西进行互动。胚胎从单细胞发育为成熟有机体的过程中，会经历好几个生长阶段（人类有几十个），每个都与前一个略有不同。最终，受精卵繁衍出各种不同的细胞，包括心脏、肝脏和脑部的细胞。
 这样的原理成为了冯·诺依曼一些设计的出发点。他曾精确地设计了一个被称为“通用复制器”的数学模型。它包括三个基本组成部分 ：机器A是一台可以根据指令整合资源并进行组装的机器 ；程序B能够指挥机器A ；主程序C可以指挥A来制造A+B+C。从技术上讲，它是一台元胞自动机，可以从周围随机散落的碎片中获取零件。原则上，根据他的设计，我们可以用现代技术造出一个3D打印与计算机的混合系统，它能够收集材料来制作你想要的东西或复制其自身。通过精心设计故意犯错的程序或宽松的质量控制，我们也能解锁生命的另一个秘密——变异。

第四周：

 Composition作为单子的反差，描述的是故事的结构，是复杂系统的总体。水波先分后合的这种形状的变化能够启发一个5岁的小孩（Ted Nelson），并促成他在数十年后创造改变世界的网络系统。所有语言只有4种领域：algebra, boolen,key-value,composition.这4种领域支撑起了复杂结构的所有信息。 用隐喻来明确如何进行超越学科的认知，这样不同学科之间也可以对比。通过命名可以加强人物地名的功能性设定。函数的对象是单个对象，函子对象是系统，自然转换则是比较比较的方法。在函数映射中一个单一的箭头可以分化成若干个压缩前的千丝万缕的箭头。在函子映射中，一个箭头包含了对元素的映射和对元素关系的映射。修订这样映射规则的过程，就是产生更新的范式。
 课程上我们讨论了这些问题：
 （1）函数：A是阿斗，B是刘备。那么A到B，阿斗和刘备的关系是什么。答:刘备是阿斗的爸爸，刘备把位置让给了阿斗。
 （2）函子：S为孙吴，T为曹营。比较S和T之间的关系：答: 孙吴系统犯下了曹魏系统犯过的错
 （3）自然转换：S为创业，T为统一大业，S到T的不同路径进行一下比较。答:从创业到统一或者把所有竞争者都干掉，或者是使用吞并的方法，把所有的敌人都变成自己的人。相互比较后发现，第二种方法更加的和谐。如：曹操使用挟天子以令诸侯的方法来实现统一大业，而其他的政治集团有的使用强行征战的方法，曹操的方法显得更加的阴险，而其他的政治集团的方法显得更加的光明正大。  
 范畴论：水平垂直两种截然不同的复合方式，horizental composition vertical composition。然后讲到了一个图，左边的图和右边图将保持相似的结构，自我感觉范畴论其实就是函数的相互映射，以及映射的映射。越到上层压缩性会变得越高，于是变得更加的抽象，可以使用越来越复杂的矩阵来将之进行运算。对于一个无限复杂的工程问题可以通过范畴论进行相应的化简。
 范畴论之中最为关键的思路是幺元，把所有的东西都放在矩阵之中进行运算，范畴论会被计算科学界用来作为一个编程的工具，范畴论将会被计算科学界用来简化计算的流程，如何才可以将一个复杂的系统进行简化，当所有的名词在人脑之中放不下的时候，我们可以使用范畴论，将他按照一定的方式进行排列整理，使用维基词典进行整理。

第五周：

 文字、会计法则、对称性、与认知能力的演进彼此相关。文字的发明来自记账的需求，知识的传承建立在可表达性上。文字、账目明细、可比对的结构或数据: 创造可重复表达现象的条件。数据的验证方法: 数据内容的差异性，内容的不可篡改性。最“小”的信息（可表达差异性的符号）单位是量子(Quantum)。命名空间的计量方式是枚举系统结构的方法。复式记账、会计平衡公式、逻辑结构的复合与拆解与近代数学与科学方法相关。这样的表达需要具备可靠性（soundness）和完备性（Completeness）。
 目前，许多学科都可以用相应的箭头来描述，从而构建相应的框架。我们可以利用等式和箭头，建立会计学与物理学之间的联系。在会计学中：
                         A（资产）=L（负债）+SE（所有者权益）
 而在物理学中：
                         H（哈密顿量）=T（动能）+V（势能）
 物理学和会计学在此公式上的惊人相似表明所有学科实际共有一套相同的语言表达体系。

科学革命的结构的读后感

Chapter 2

 Paradigms are theories created by one of the pre-paradigm schools. Though the author gives description rather than explanation of the arduous process of acquiring paradigms, we can conclude that when some theories are universally accepted, and can attract an enduring group of adherents away from competing modes of scientific activity, paradigms that prove able to guide the whole group’s research emerge all of a sudden.
 The emergence of a paradigm contributes to scientific inquiry in seven aspects. First, it makes both fact collection and theory articulation highly directed activities, so scientists no longer explore nature casually or at random. Second, it suggests which experiments will be worth performing so scientists are confident what they are studying is highly relevant. Third, the end of interschool debate ends the constant reiteration of fundamentals. The confidence that they are on the right track encouraged scientists to undertake more precise, esoteric, and consuming sorts of work. Fourth, it transforms a group previously interested merely in the study of nature into a profession or a discipline. Fifth, it marks the beginning of specific classification. Sixth, it creates advanced systems that improve effectiveness and efficiency, in particular, for esoteric work. Above all, it produces scientific community whose members push on to more concrete and recondite problems, and increasingly they report their results in articles addressed to other electricians.
 Ultimately, the emergence of a paradigm is invariably followed by a truth boom, as truth emerges more readily from error than from confusion.

Chapter 3

 Although paradigms have shown to be particularly revealing of the nature, the match between facts and theories is still imperfect, and scientists have to avoid approximations and obtain satisfactory agreements.
 To do this, they need to answer the following questions. First, how to conduct empirical works to articulate the paradigm? Second, what further explorations relative to theoretical works can they make to classify theoretical problems of normal science? Third, how to use existing theories to predict factual information of intrinsic value?
 All their efforts serve for the reformulation of a paradigm: to articulate the paradigm elegantly and logically in mathematics, which is both theoretical and experimental. The desire for acknowledgement and the ambition for fame ensure scientists to pursue the same goal. Driven by anthropic ultimate curiosity about the nature, they are committed to solve the problems after the acquisition of the paradigm. 
 The problems always exist, as a successful paradigm is not, however, to be either completely successful with a single problem or notably successful with any large number.

Chapter 4

  What are characteristics of normal science?
  Normal science shares paralleled characteristics with puzzle-solving. First, it offers challenging problems as puzzles that can test ingenuity or skill in solution and thus drive scientists on. Second, the criterion of these problems is the assured existence of a solution, but on the contrary, has nothing to do with the intrinsic value of their outcome. Third, these puzzles are invariably so attractive that scientists attack them with remarkable passion and devotion, holding the conviction that, if only they are skillful enough, they will succeed in solving a puzzle that no one before has solved or solved so well. It is very much the same thing as a child is immersed in solving crossword puzzles that may not give him any benefit.
  Above all, like puzzle-solving, normal science has rules. In the same way as all the pieces must be used before you solve a jigsaw puzzle, until certain conditions have been satisfied, no problem can be solved. Rules play the role of established viewpoint or preconception that bound the admissible solutions to theoretical problems. Under the influence of rules, scientists adopt the attitude that the results of their researches must fall into a narrow range that the paradigm restricts. As a child must obey rules in his games without fail, all these rules have undoubtedly held for scientists at all times.

Chapter 5

  We can account for the priority of paradigms in four aspects. First, rules are abstracted from their more global paradigms and deployed. However, the existence of a paradigm is independent on the existence of rules and need not even imply that any full set of rules exists.
  Second，paradigms can be determined easily, and they can determine normal science directly without the intervention of discoverable rules or assumptions. They are more binding and more complete when it comes to the definitions of basic concepts. Thanks to paradigms, we can understand what makes a particular problem or solution legitimate almost intuitively.
  Third, in the absence of rules, normal science can still proceed under the guidance of paradigms that direct research. As long as paradigms remain secure, however, they can function without agreement over rationalization or without any attempted rationalization at all.
  Fourth, Explicit rules, when they exist, are usually common to a very broad scientific group, but paradigms need not be. They are quite irrelevant and related to each other to a very limited extent, so they need not stand or fall tegother.
  In a nutshell, rules cannot exhaust all functions of paradigms and it is flexible and subject to change. While paradigms might be intangible and artificial, they have absolute dominance over rules.

Chapter 6

 I want to give my account of crisis at the close of a paradigm.
 The close of a paradigm is noncumulative as the threat it face is abruptly posed by a problem that the paradigm fails to solve. After all efforts to reconcile this problem with the paradigm are in vain, this novelty will be claimed incompatible with the basic assumptions of the paradigm. Crisis then occurs with destructive changes in beliefs about nature. Scientists pronounce their failure in saving the paradigm from breakdown, and feel obliged to desert it. A crisis is an occasion for retooling because the tools supplied by the original paradigm prove uncapable of solving all problems. 
 In my opinion, the use of “crisis” is reasonable in a second way. Scientists run the risk of being wrong when they persuade themselves to make the tough decision to convert their beliefs. Together with science, scientists themselves are passing through a grave crisis.

Chapter 7

 In this chapter, Kuhn discusses response to crisis.
 Kuhn first lists two reasons for doubting that scientists reject paradigms because confronted with anomalies. First is that scientists do not renounce the paradigm that has led them into crisis while they consider alternatives and second is that they can actually devise numerous articulations to eliminate any apparent conflict.
 So why do scientists reject paradigms? He notes that to reject one paradigm goes hand in hand with substituting another. Scientists see puzzles as a source of crisis only when from another viewpoint. To make this possible, an anomaly must usually be more than just an anomaly. Kuhn applies a few examples to illustrate how the transition to crisis and to extraordinary science is evoked. 
 Kuhn claims two effects of crisis are universal and crisis are noncumulative. In the end, a transition from normal to extraordinary research results in scientific revolution, which, from my perspective, is the ultimate response to crisis.

Chapter 8

 Kuhn brings up a question:” Why should a change of paradigm be called a revolution?” and outlines the parallelism between scientific and political revolution.
 First, he describes the feature of a scientific revolution: it is noncumulative and the paradigms involved are incompatible. The striking similarity between the characteristics regarding the process of political revolution and scientific revolution are that they begin with a growing sense that existing systems have ceased to meet certain problems. The awareness breeds dissatisfaction. They aim to change the status quo in ways that are prohibited.
 Second, like competing political institutions, competing paradigms proves to be fundamentally incompatible modes. Paradigmatic differences cannot be reconciled.
 Third, the assimilation of either a new sort of phenomenon or a new scientific theory must demand the rejection of an older paradigm, which would make scientific revolution genuinely cumulative otherwise.
 Fourth, Kuhn refutes logical positivist view, arguing that the logical positivist view makes any theory ever used by a significant group of competent scientists immune to attack.
 In the end, since paradigms cannot settle their differences. It is inevitable that they will talk through each other. The results of debates are determined by external criteria. And this recourse to external criteria most obviously makes paradigm debates revolutionary.