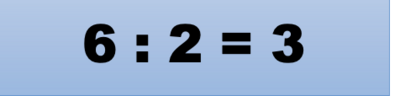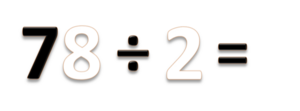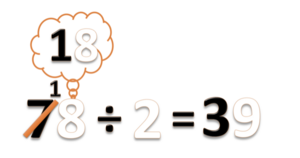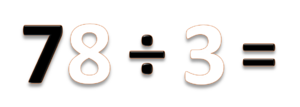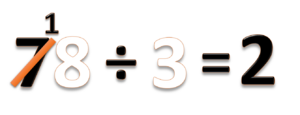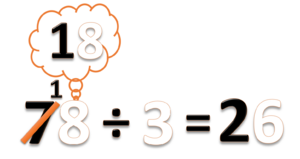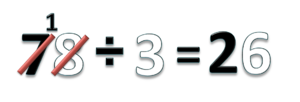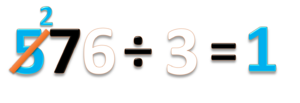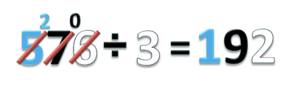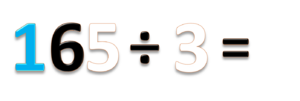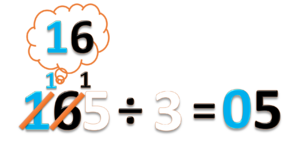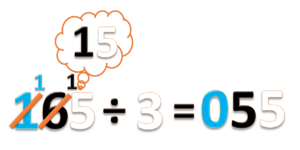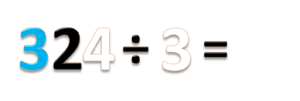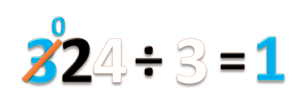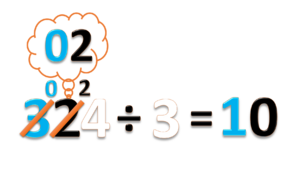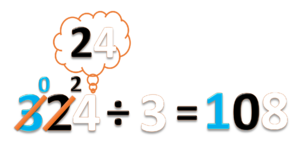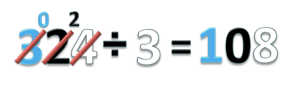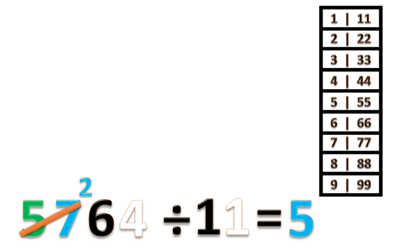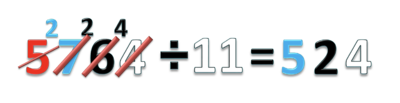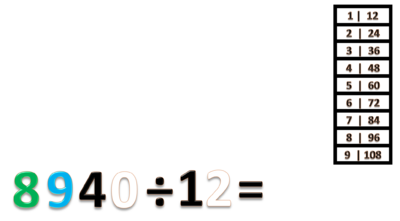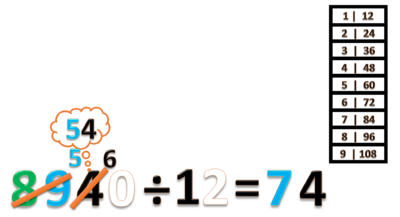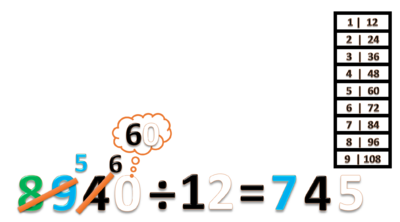Difference between revisions of "GABER Pembagian"
m (Text replacement - "{{#ev:youtube|hP3ENPc8Jf0 |width=900 |height=500 }} " to "{{#widget:YouTube |id= hP3ENPc8Jf0 |width= 900 |height=500 }}") |
|||
| Line 360: | Line 360: | ||
{{#widget:YouTube | {{#widget:YouTube | ||
|id=zclncyxtBS4 | |id=zclncyxtBS4 | ||
|width=900 | |{{#widget:YouTube | ||
|id= hP3ENPc8Jf0 | |||
|width= 900 | |||
|height=500 | |height=500 | ||
}}|height=500 | |||
|start=10|end=120 | |start=10|end=120 | ||
}} | }} | ||
| Line 569: | Line 572: | ||
{{#widget:YouTube | {{#widget:YouTube | ||
|id=jEJywjpVOck | |id=jEJywjpVOck | ||
|width=900 | |{{#widget:YouTube | ||
|id= hP3ENPc8Jf0 | |||
|width= 900 | |||
|height=500 | |height=500 | ||
}}|height=500 | |||
}} | }} | ||
| Line 714: | Line 720: | ||
{{#widget:YouTube | {{#widget:YouTube | ||
|id=lb3p1LjYAxg | |id=lb3p1LjYAxg | ||
|width=900 | |{{#widget:YouTube | ||
|id= hP3ENPc8Jf0 | |||
|width= 900 | |||
|height=500 | |height=500 | ||
}}|height=500 | |||
|start=10|end=120 | |start=10|end=120 | ||
}} | }} | ||
Revision as of 05:07, 13 January 2024
GASING Berhitung: Pembagian
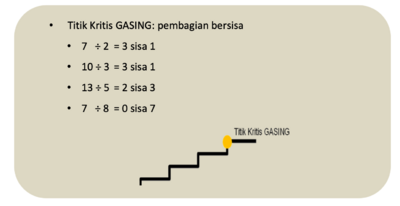
- Titik kritis Gasing Pembagian
- Titik kritis Gasing dalam pembagian adalah kondisi dimana siswa mampu melakukan pembagian bersisa secara mencongak.
Untuk mencapai titik kritis gasing siswa harus melalui tahapan-tahapan sebagai berikut:
- Mengenal arti pembagian
- Pembagian bilangan dengan bilangan 1 angka, hasilnya berupa bilangan 1 angka. Dan Hubungannya dengan perkalian
- Pembagian bersisa.
Konsep Pembagian
- Mengenal Arti Pembagian
- Pembagian adalah proses mendistribusikan atau membagikan habis sejumlah benda kepada sejumlah wadah dimana tiap wadah mendapatkan jumlah benda yang sama.
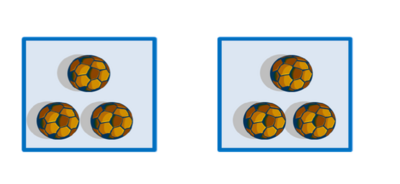
- Misalnya: ada 6 bola hendak dibagikan pada 2 kotak.
- Agar adil tiap kotak menerima 3 bola.
- Kita tuliskan proses ini sebagai 6 ÷ 2 = 3 (dibaca enam dibagi dua sama dengan tiga).
Cara mendapatkan hasil 6 ÷ 2
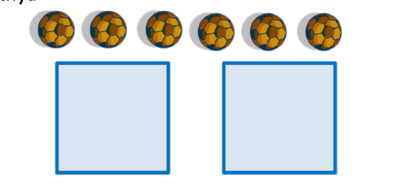
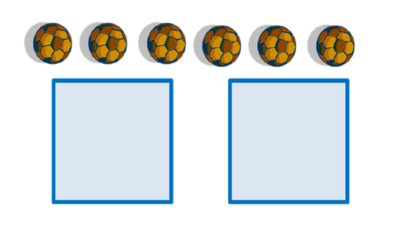
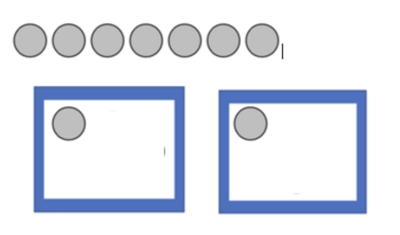
Ini ada 6 bola
- Langkah 1
- Bagikan masing-masing 1 bola ke dalam tiap kotak
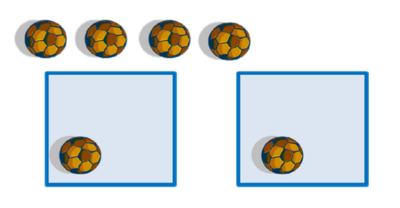
- Langkah 2
- Bagikan lagi masing-masing 1 bola dalam tiap kotak.
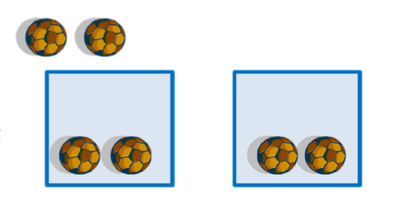
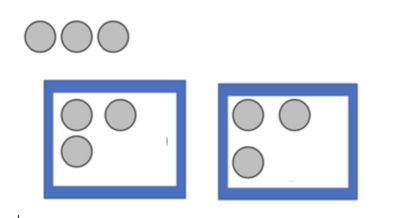
- Langkah 3
- Bagikan lagi masing-masing 1 bola dalam tiap kotak.
- Bola sudah habis dibagikan. Tiap kotak menerima 3 bola.
- Dengan demikian kita katakan bahwa 6 ÷ 2 =3
Catatan: 6 ÷ 2 = dapat diartikan sebagai berapa benda diterima oleh tiap kotak jika 6 benda dibagikan secara adil (merata) pada 2 kotak.
Atau: ada 6 benda hendak dibagikan secara adil dalam 2 kotak, berapa isi masing-masing kotak.
Pembagian bilangan dengan bilangan 1 angka, hasilnya bilangan 1 angka
Pada bagian ini akan dibagi menjadi 2 bagian, yaitu:
- 1. Pembagian bilangan dengan bilangan 1 angka tetapi hasilnya juga 1 angka dan tidak bersisa (habis :dibagi).
- 2. Pembagian bilangan dengan bilangan 1 angka tetapi hasilnya juga 1 angka dan bersisa (tidak habis :dibagi).
Bagian 1: Pembagian bilangan dengan bilangan 1 angka tetapi hasilnya juga 1 angka dan tidak bersisa (habis :dibagi)
KONKRET
Ingat kembali arti pembagian yaitu membagikan sejumlah benda dalam beberapa wadah di mana isi dalam setiap wadah harus sama.
- Misalnya kita menghitung secara konkret nilai dari enam dibagi dua.
Caranya adalah sebagai berikut:
- Langkah 1
- Bagikan masing-masing 1 bola ke dalam tiap kotak
- Langkah 2
- Bagikan lagi masing-masing 1 bola dalam tiap kotak.
- Langkah 3
- Bagikan lagi masing-masing 1 bola dalam tiap kotak.
- Bola sudah habis dibagikan. Tiap kotak menerima 3 bola.
- Jadi enam dibagi dua adalah tiga.
ABSTRAK
Bentuk abstrak dari pembagian di atas adalah
MENCONGAK
Untuk melakukan mencongak pembagian, kita akan memanfaatkan konsep perkalian.
Coba perhatikan hal berikut
- Arti 6 ÷ 2 = adalah ada 6 benda hendak dimasukan/dibagikan secara adil dalam 2 kotak, berapa isi tiap kotak?
- Arti 2 x ... = 6 adalah ada 2 kotak masing-masing harus di isi berapa benda agar jumlahnya ada 6 benda?
Kalau dipikir kedua kalimat diatas bermakna sama. Yaitu sama-sama menghitung isi kotak.
Karena kita sudah belajar perkalian, maka untuk menghitung cepat pembagian, kita memanfaatkan ilmu perkalian kita.
Dengan demikian kita bisa menghitung pembagian dengan sangat cepat.
- Jadi kalau kita mau menghitung 12:4 =
- Maka yang kita perlu pikirkan adalah 4 kali berapa hasilnya 12.
- Jawabnya adalah 3
- Dengan demikian 12:4 = 3
Agar siswa mahir dalam mencongak pembagian maka ajarkan siswa melakukan kegiatan berikut
- Pembagian 9
- Kita ingatkan dulu
- 9 x ... = 9
- 9 x ... = 18
- 9 x ... = 27
- 9 x ... = 36
- 9 x ... = 45
- 9 x ... = 54
- 9 x ... = 63
- 9 x ... = 72
- 9 x ... = 81
- 9 x ... = 90
Kemudian baru kita ajarkan
- 9 ÷ 9 =
- 18 ÷ 9 =
- 27 ÷ 9 =
- 36 ÷ 9 =
- 45 ÷ 9 =
- 54 ÷ 9 =
- 63 ÷ 9 =
- 72 ÷ 9 =
- 81 ÷ 9 =
- 90 ÷ 9 =
- Pembagian 8
- Kita ingatkan dulu
- 8 x ... = 8
- 8 x ... = 16
- 8 x ... = 24
- 8 x ... = 32
- 8 x ... = 40
- 8 x ... = 48
- 8 x ... = 56
- 8 x ... = 64
- 8 x ... = 72
- 8 x ... = 80
Kemudian baru kita ajarkan
- 8 ÷ 8 =
- 16 ÷ 8 =
- 24 ÷ 8 =
- 32 ÷ 8 =
- 40 ÷ 8 =
- 48 ÷ 8 =
- 56 ÷ 8 =
- 64 ÷ 8 =
- 72 ÷ 8 =
- 80 ÷ 8 =
- Pembagian 7
- Kita ingatkan dulu
- 7 x ... = 7
- 7 x ... = 14
- 7 x ... = 21
- 7 x ... = 28
- 7 x ... = 35
- 7 x ... = 42
- 7 x ... = 49
- 7 x ... = 56
- 7 x ... = 63
- 7 x ... = 70
Kemudian baru kita ajarkan
- 7 ÷ 7 =
- 14 ÷ 7 =
- 21 ÷ 7 =
- 28 ÷ 7 =
- 35 ÷ 7 =
- 42 ÷ 7 =
- 49 ÷ 7 =
- 56 ÷ 7 =
- 63 ÷ 7 =
- 70 ÷ 7 =
Kita ingatkan dulu 6 x ... = 6 6 x ... = 12 6 x ... = 18 6 x ... = 24 6 x ... = 30 6 x ... = 36 6 x ... = 42 6 x ... = 48 6 x ... = 54 6 x ... = 60 Kemudian kita ajarkan 6 ÷ 6 = 12 ÷ 6 = 18 ÷ 6 = 24 ÷ 6 = 30 ÷ 6 = 36 ÷ 6 = 42 ÷ 6 = 48 ÷ 6 = 54 ÷ 6 = 60 ÷ 6 =
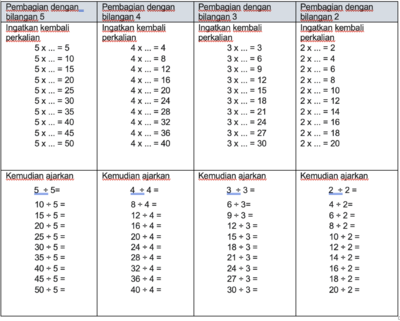
Lakukan ini untuk perkalian/pembagian 5, 4, 3, 2, dan 1 seperti pada tabel dibawah ini
Aktivitas 1a mencongak
- Siswa dilatih secara cepat mencongak pembagian dengan bilangan 1 angka seperti diajarkan diberikan di atas.
Aktivitas 1b berlatih pembagian dengan bilangan 1 angka
- Tujuan: Siswa menuliskan dengan cepat hasil pembagian dengan bilangan 1 angka
- Siswa mengerjakan dari buku Pengurangan dan Pembagian (buku 3) Latihan 10, 11a-b
Bagian 2 : Pembagian bilangan dengan bilangan 1 angka tetapi hasilnya juga 1 angka dan bersisa (tidak habis dibagi)
Disini Kita akan belajar pembagian dengan bilangan 1 angka tetapi ada sisanya.
Misalnya kita akan menghitung hasil pembagian 9 : 2
KONKRET
Terdapat 9 benda yang akan dibagikan sama banyak ke dalam 2 kotak.
Bagikan masing-masing 1 benda ke dalam tiap kotak
Bagikan kembali masing-masing 1 benda ke dalam tiap kotak
Bagikan kembali masing-masing 1 benda ke dalam tiap kotak
Bagikan kembali masing-masing 1 benda ke dalam tiap kotak
- Kita lihat bahwa tiap kotak berisi 4 benda. Tapi masih ada sisa 1.
- Kita tuliskan 9 ÷ 2 = 4 sisa 1 (dibaca Sembilan dibagi dua adalah 4 sisa 1)
Selanjutnya kita minta siswa melakukan eksplorasi dengan menggunakan kelereng dan kotak untuk melakukan pembagian 2
- 3 ÷ 2 =
- 5 ÷ 2 =
- 7 ÷ 2 =
- 9 ÷ 2 =
- 11 ÷ 2 =
- 13 ÷ 2 =
- 15 ÷ 2 =
- 17 ÷ 2 =
Kemudian minta siswa menyimpulkan bagaimana cara cepat untuk menghitung pembagian bersisa ini?
Cara cepatnya adalah dengan mencari bilangan apa yang kalau dikalikan dengan bilangan pembagi hasilnya lebih kecil dan paling dekat dengan bilangan yang dibagi.
Misalnya 17 ÷ 2 = , untuk menjawab ini kita mencari bilangan apa yang dikalikan 2 hasilnya lebih kecil dan paling dekat dengan 17.
Kita coba 6 x 2 = 12, terlalu jauh dari 17 Coba 7 x 2 = 14, sudah lebih dekat ke 17 Coba 8 x 2 = 16, Lebih dekat ke 17 Coba 9 x 2 = 18, terlalu besar, melebihi 17.
Jawabnya 17 ÷ 2 = 8, untuk mencari sisanya kita kurangkan 17 dengan 16 (bilangan terdekat dengan 17 dan bisa habis dibagi 2) yaitu 17 - 16 = 1
Jadi 17 ÷ 2 = 8 sisa 1
Kita latih berulang-ulang pembagian dengan 2 ini, kemudian pembagian dengan 10 (karena mudah mencari sisanya). Lanjutkan dengan pembagian 5. Setelah mahir baru kita berlatih untuk pembagian lainnya.
Beberapa contoh
- 46 ÷ 10 = ...
- Siswa mencari bilangan apa yang dikalikan 10 mendekati 46
- coba 3 x 10 = 30 masih jauh dari 46
- coba 4 x 10 = 40 sudah dekat 46
- coba 5 x 10 = 50 lebih dari 46
- Jawabnya 46 ÷ 10 = 4 dengan sisa 6. Sisa diperoleh dari 46 dikurangi bilangan yang lebih kecil dan paling dekat 46. Sisa = 46 - 40 = 6
- Jadi 46 ÷ 10 = 4 sisa 6
- 57 ÷ 10 =
- 36 ÷ 10 =
- 81 ÷ 10 =
- 92 ÷ 10 =
- 45 ÷ 10 =
- 68 ÷ 10 =
- dst...
Berikut pembagian dengan 5
- 17 ÷ 5 =
- 12 ÷ 5 =
- 23 ÷ 5 =
- 27 ÷ 5 =
- 36 ÷ 5 =
- 48 ÷ 5 =
- dst...
- Usahakan anak-anak mahir dalam mencongak pembagian bersisa ini.
Aktivitas 2 berlatih pembagian bersisa
- Tujuan: Siswa menuliskan dengan cepat hasil pembagian bersisa
- Siswa mengerjakan dari buku Pengurangan dan Pembagian (buku 3) Latihan 13a-c
Video ini menunjukan bagaimana anak-anak dapat mencongak pembagian dengan bilangan 1 angka.
Pembagian sebarang bilangan dengan bilangan 1 angka
Dengan menguasai pembagian bersisa maka pembagian suatu bilangan dengan bilangan 1 angka ini sangat mudah.
Mari kita lihat beberapa contoh
- a) 78 ÷ 2 =
- Bilangan 78 terdiri dari 7 puluhan dan 8 satuan
- Bagi puluhannya, 7 ÷ 2 = 3 sisa 1
- Tulis hasil baginya 3 (angka 3 ini artinya 3 puluhan)
- Sisanya 1 puluhan
- Tulis sisanya. di antara angka 7 dan 8
- Jangan lupa coret angka 7 (sebagai tanda bahwa kita sudah menyelesaikan pembagian 7 puluhan ini).
- Sekarang kita punya sisa 1 puluhan
- Kita juga punya 8 satuan.
- 1 Puluhan + 8 satuan = 18 satuan.
- Hasilnya ini bagi dengan 2.
- 18 ÷ 2 = 9
- Tulis hasilnya 9 pada nilai tempat satuan
- Jangan lupa coret tangka 8 sebagai tanda bahwa 8 satuan ini juga sudah selesai dibagi).
- Jadi 78 ÷ 2 = 39
- b) 78 ÷ 3 =
- Bilangan 78 terdiri dari 7 puluhan dan 8 satuan
- Bagi puluhannya, 7 ÷ 3 = 2 sisa 1
- Tulis hasil baginya 2 (angka 2 ini artinya 2 puluhan)
- Tulis sisanya diantara angka 7 dan 8.
- Jangan lupa coret angka 7 (sebagai tanda bahwa kita sudah menyelesaikan pembagian 7 puluhan ini).
- Sekarang kita punya sisa 1 puluhan
- Kita juga punya 8 satuan.
- Gabungkan ini menjadi 18 satuan. Lalu bagi dengan 3.
- 18 ÷ 3 = 6
- Tulis hasilnya 6 pada nilai tempat satuan
- Jangan lupa coret tangka 8 sebagai tanda bahwa 8 satuan ini juga sudah selesai dibagi).
- Jadi 78 ÷ 3 = 26
- c) 576 ÷ 3 =
- Bilangan 576 terdiri dari 5 ratusan (biru) 7 puluhan (hitam) dan 6 satuan (putih)
- Bagi ratusannya, 5 ÷ 3 = 1 sisa 2
- Tulis hasil baginya 1.
- Tulis sisanya 2 diantara angka 5 dan 7
- Coret angka 5.
- Sekarang kita punya sisa 2 ratusan
- Kita juga punya 7 puluhan
- Gabungkan ini menjadi 27 puluhan. Lalu bagi dengan 3.
- 27 ÷ 3 = 9 sisa 0.
- Tulis hasilnya 9 pada nilai tempat puluhan
- tulis sisanya 0, diantara angka 7 dan 6
- Jangan lupa coret angka 7
- Kita punya sisa 0 puluhan
- Kita juga punya 6 satuan.
- Gabungkan ini menjadi 06 satuan atau 6 satuan. Lalu bagi dengan 3.
- 6 ÷ 3 = 2
- Tulis hasilnya 2 pada nilai tempat satuan
- Jangan lupa coret angka 6
- Jadi 576 ÷ 3 = 192
- d) 165 ÷ 3 =
- Bilangan 165 terdiri dari 1 ratusan (biru) 6 puluhan (hitam) dan 5 satuan (putih)
- Bagi ratusannya, 1 ÷ 3 = 0 sisa 1
- Tulis hasil baginya 0.
- Tulis sisanya 1 diantara angka 1 dan 6.
- Jangan lupa coret angka 1.
- Sekarang kita punya sisa 1 ratusan
- Kita juga punya 6 puluhan
- Gabungkan ini menjadi 16 puluhan. Lalu bagi dengan 3.
- 16 ÷ 3 = 5 sisa 1.
- Tulis hasilnya 5 pada nilai tempat puluhan
- tulis sisanya 1, diantara angka 6 dan 5
- Jangan lupa coret angka 6.
- Kita punya sisa 1 puluhan
- Kita juga punya 5 satuan.
- Gabungkan ini menjadi 15 satuan. Lalu bagi dengan 3.
- 15 ÷ 3 = 5
- Tulis hasilnya 5 pada nilai tempat satuan
- Jangan lupa coret angka 5.
- Jadi 165 ÷ 3 = 055 atau 55
- e) 324 ÷ 3 =
- Bilangan 324 terdiri dari 3 ratusan (biru) 2 puluhan (hitam) dan 4 satuan (putih)
- Bagi ratusannya, 3 ÷ 3 = 1 sisa 0
- Tulis hasil baginya 1.
- Tulis sisanya 0. di antara angka 3 dan 2.
- Jangan lupa coret angka 3.
- Sekarang kita punya sisa 0 ratusan
- Kita juga punya 2 puluhan
- Gabungkan ini menjadi 02 puluhan atau 2 puluhan. Lalu bagi dengan 3.
- 2 ÷ 3 = 0 sisa 2.
- Tulis hasilnya 0 pada nilai tempat puluhan
- tulis sisanya 2, diantara angka 2 dan 4.
- Jangan lupa coret angka 2.
- Kita punya sisa 2 puluhan
- Kita juga punya 4 satuan.
- Gabungkan ini menjadi 24 satuan. Lalu bagi dengan 3.
- 24 ÷ 3 = 8
- Tulis hasilnya 8 pada nilai tempat satuan
- Jangan lupa coret angka 4.
- Jadi 324 ÷ 3 = 108
- f) bagaimana 1200 ÷ 4 = ?
- Untuk bilangan yang diikuti dengan banyak nol, cara pembagiannya adalah kita lakukan pembagian untuk bilangan yang bukan nol.
- Kemudian kita tambahkan nol dibelakangnya.
- Untuk 1200 ÷ 4 =
- 12 ÷ 4 = 3
- Dibelakang 12 ada dua nol. Maka hasilnya ada 3 diikuti dengan 2 nol dibelakangnya yaitu 300
- Jadi 1200 ÷ 4 = 300
- Kita bisa membuktikan juga ini dengan menggunakan cara a sampai e diatas.
Untuk beberapa contoh pembagian dengan bilangan 1 angka dapat dilihat di video berikut
Aktivitas 3 berlatih pembagian dengan bilangan 1 angka
- Tujuan: Siswa menuliskan dengan cepat hasil pembagian dengan bilangan 1 angka
- Siswa mengerjakan dari buku Pengurangan dan Pembagian (buku 3) Latihan 12 dan 14a-c
Pembagian dengan bilangan 2 angka
Konsep pembagian dengan bilangan 2 angka hampir sama seperti pembagian dengan bilangan 1 angka.
Untuk jelasnya mari kita lihat contoh berikut
- a) 5764 ÷ 11 = ...
- Langkah pertama adalah kita membuat tabel perkalian 11
Cara membuatnya adalah dengan melakukan penjumlahan berulang:
- 11
- 11 + 11 = 22
- 22 + 11 = 33
- 33 + 11 = 44
- 44 + 11 = 55
- 55 + 11 = 66
- 66 + 11 = 77
- 77 + 11 = 88
- 88 + 11 = 99
- Bagi ribuannya, 5 ÷ 11 = 0 sisa 5
- Kita boleh juga ambil ribuan dan ratusan sekaligus (hanya untuk pembagian pertama saja)
- untuk itu ubah 5 ribuan jadi 50 ratusan
- Jadi disini kita punya 57 ratusannya
- Bagi ratusannya 57 : 11 = 5 sisa 2 (gunakan tabel perkalian 11)
- Tulis hasil baginya 5 (angka 5 ini adalah mempunyai nilai tempat ratusan)
- Tulis sisanya 2. di antara angka 7 dan 6
- Jangan lupa coret angka 5 dan 7
- Sekarang kita punya sisa 2 ratusan
- Kita juga punya 6 puluhan
- Gabungkan ini menjadi 26 puluhan. Lalu bagi dengan 11.
- 26 ÷ 11 = 2 sisa 4 (gunakan tabel perkalian 11)
- Tulis hasilnya 2 pada nilai tempat puluhan
- tulis sisanya 4, diantara angka 6 dan 4
- Jangan lupa coret angka 6
- Kita punya sisa 4 puluhan
- Kita juga punya 4 satuan.
- Gabungkan ini menjadi 44 satuan. Lalu bagi dengan 11.
- 44 ÷ 11 = 4 (gunakan tabel perkalian 11).
- Tulis hasilnya 4 pada nilai tempat satuan
- Jangan lupa coret angka 4
- Jadi 5764 ÷ 11 = 524
Berikan banyak contoh pembagian dengan 11 ini. Ini bisa dilakukan tanpa membuat table perkalian 11 karena perkalian 11 ini mudah.
- b) 8940 ÷ 12 = ...
- Langkah pertama adalah kita membuat table perkalian 12
Caranya adalah dengan melakukan penjumlahan berulang
- 12
- 12 + 12 = 24
- 24 + 12 = 36
- 36 + 12 + 48
- 48 + 12 = 60
- 60 + 12 = 72
- 72 + 12 = 84
- 84 + 12 = 96
- 96 + 12 = 108
- Kita ambil 2 angka pertama 89
- Ubah 8 ribuan jadi 80 ratusan
- Jadi kita punya 80 ratusan + 9 ratusan = 89 ratusan
- Bagi ratusannya 89 : 12 = 7 sisa 5 (gunakan tabel perkalian 12)
- Tulis hasil baginya 7.
- Tulis sisanya 5. Diantara angka 9 dan 4
- Jangan lupa coret angka 8 dan 9.
- Sekarang kita punya sisa 5 ratusan
- Kita juga punya 4 puluhan
- Gabungkan ini menjadi 54 puluhan. Lalu bagi dengan 12.
- 54 ÷ 12 = 4 sisa 6 (gunakan tabel perkalian 12)
- Tulis hasilnya 4 pada nilai tempat puluhan
- tulis sisanya 6, diantara angka 4 dan 0.
- Jangan lupa coret angka 4
- Kita punya sisa 6 puluhan
- Kita juga punya 0 satuan.
- Gabungkan ini menjadi 60 satuan. Lalu bagi dengan 12.
- 60 ÷ 12 = 5 (gunakan tabel perkalian 12).
- Tulis hasilnya 5 pada nilai tempat satuan
- Jangan lupa coret angka 0.
- Jadi 8940 ÷ 12 = 745
Untuk pembagian dengan bilangan 2 angka dapat dilihat contohnya di video berikut
Pembagian dengan bilangan 3 angka atau lebih bisa dilakukan dengan cara yang sama yaitu dengan membuat tabel perkalian dulu.
Aktivitas 4 berlatih pembagian dengan bilangan 2 angka
- Tujuan: Siswa menuliskan dengan cepat hasil pembagian dengan bilangan 2 angka
- Siswa mengerjakan dari buku Pengurangan dan Pembagian (buku 3) Latihan 15 dan 16