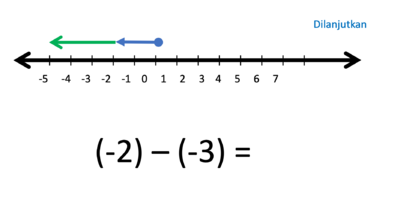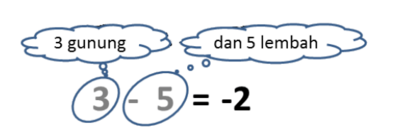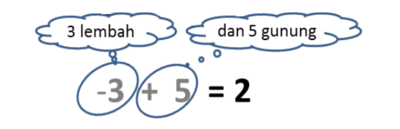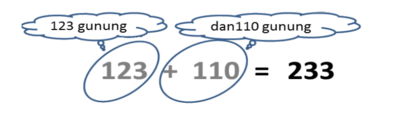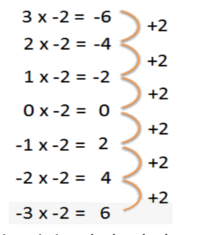Difference between revisions of "G COUNTING 5 : Whole Number"
Yohanespkc (talk | contribs) |
Yohanespkc (talk | contribs) |
||
| Line 760: | Line 760: | ||
b) 3 x (-2)=.... | : b) 3 x (-2)=.... | ||
:: 3 x (-2) artinya 3 kotak isi 2 lembah (dari definisi perkalian) | :: 3 x (-2) artinya 3 kotak isi 2 lembah (dari definisi perkalian) | ||
[[Image:Screen Shot 2022-02-11 at 15.26. | |||
[[Image:Screen Shot 2022-02-11 at 15.26.27.png|400px]] | |||
:: Hasilnya adalah 2 lembah + 2 lembah + 2 lembah = 6 lembah | :: Hasilnya adalah 2 lembah + 2 lembah + 2 lembah = 6 lembah | ||
| Line 770: | Line 771: | ||
: c) (-3) × 2 =.... | |||
: 3 x 2 artinya ada 3 kotak isinya masing-masing 2 gunung | |||
: (-3) x 2 artinya ada 3 anti kotak isinya masing-masing 2 gunung | |||
: Disini kita belajar konsep anti kotak. | |||
: Anti kotak mengubah gunung menjadi lembah | |||
: Anti kotak mengubah lembah menjadi gunung | |||
Hasilnya | :: Dalam anti kotak terdapat 2 gunung + 2 gunung + 2 gunung = 6 gunung | ||
:: Anti kotak akan merubah gunung jadi lembah | |||
:: Hasilnya adalah 6 lembah | |||
:: (-3) x 2 = -6 | |||
Cara lain | |||
: Melihat Pola | |||
[[Image:Screen Shot 2022-02-11 at 15.27.10.png|400px]] | [[Image:Screen Shot 2022-02-11 at 15.27.10.png|400px]] | ||
Yang pertama dengan menggunakan alat peraga gunung dan lembah. Kita mulai dengan 3 x 2. Seperti disampaikan di atas, ini berarti kita MENARUH 2 gunung sebanyak 3 kali. Hasilnya 6 gunung, jadi 3 x 2 = 6. Lalu 2 x 2 artinya kita menaruh 2 gunung sebanyak 2 kali. Hasilnya 4 gunung, jadi 2 x 2 = 4. Lalu 1 x 2 artinya kita menaruh 2 gunung sekali. Hasilnya 2 gunung, jadi 1 x 2 = 2. Kemudian 0 x 2, artinya kita tidak melakukan apa-apa jadi nilainya 0. Sekarang – 1 x 2 artinya kita MENGAMBIL 2 gunung sekali, jadi seperti konkret untuk 0 – 2, terlihat hasilnya 2 lembah, jadi -1 x 2 = -2. Untuk -2 x 2 artinya kita mengambil 2 gunung sebanyak 2 kali, jadi tersisa 4 lembah, jadi -2 x 2 = -4. Untuk -3 x 2 artinya kita mengambil 2 gunung sebanyak 3 kali, jadi tersisa 6 lembah, jadi -3 x 2 = -6. | Yang pertama dengan menggunakan alat peraga gunung dan lembah. Kita mulai dengan 3 x 2. Seperti disampaikan di atas, ini berarti kita MENARUH 2 gunung sebanyak 3 kali. Hasilnya 6 gunung, jadi 3 x 2 = 6. Lalu 2 x 2 artinya kita menaruh 2 gunung sebanyak 2 kali. Hasilnya 4 gunung, jadi 2 x 2 = 4. Lalu 1 x 2 artinya kita menaruh 2 gunung sekali. Hasilnya 2 gunung, jadi 1 x 2 = 2. Kemudian 0 x 2, artinya kita tidak melakukan apa-apa jadi nilainya 0. Sekarang – 1 x 2 artinya kita MENGAMBIL 2 gunung sekali, jadi seperti konkret untuk 0 – 2, terlihat hasilnya 2 lembah, jadi -1 x 2 = -2. Untuk -2 x 2 artinya kita mengambil 2 gunung sebanyak 2 kali, jadi tersisa 4 lembah, jadi -2 x 2 = -4. Untuk -3 x 2 artinya kita mengambil 2 gunung sebanyak 3 kali, jadi tersisa 6 lembah, jadi -3 x 2 = -6. | ||
| Line 800: | Line 808: | ||
Cara Komutatif | Cara Komutatif | ||
Selain menggunakan pola dari perkalian, kita juga dapat mendapatkan hasil perkalian tersebut dengan menggunakan sifat komutatif dari operasi perkalian. Jadi, sebagai contoh kita dapat memperoleh hasil (-3) × 2 dari 2 × (-3) = -6. | Selain menggunakan pola dari perkalian, kita juga dapat mendapatkan hasil perkalian tersebut dengan menggunakan sifat komutatif dari operasi perkalian. Jadi, sebagai contoh kita dapat memperoleh hasil (-3) × 2 dari 2 × (-3) = -6. | ||
Itu yang dulu dipelajari waktu perkalian. Muncul pertanyaan, dari mana asal gunung tersebut? Harus ada yang menaruh. Dapat diartikan 3 x 2 sama dengan 3 kali menaruh 2 gunung: 2 gunung, 2 gunung, 2 gunung. Jadi, terdapat 6 gunung, sehingga 3 x 2 = 6. | |||
Untuk 3 x (-2) dapat diartikan 3 kali menaruh 2 lembah, jadi terdapat 6 lembah, sehingga dapat disimpulkan 3 x (-2) = -6. | |||
Untuk perkalian bilangan bulat, kalau bilangan di belakang simbol kali adalah positif artinya gunung dan kalau negatif artinya lembah. Sekarang kalau bilangan di depan simbol kali adalah positif artinya menaruh, kalau negatif artinya mengambil. Ini akan kita lihat pada jenis perkalian berikutnya. | |||
d) (-3) × (-2) = .... | d) (-3) × (-2) = .... | ||
Revision as of 06:50, 18 February 2022
Gasing Counting Introduction
Matematika selama ini telah menjadi mata pelajaran yang ditakuti banyak siswa. Siswa kesulitan ketika mengerjakan soal-soal matematika karena lemahnya kemampuan konsep matematika mereka. Untuk itu diperlukan suatu cara agar siswa tertarik dengan matematika dan dapat belajar matematika dengan mudah.
Oleh karena itu Prof.Yohanes Surya, Ph.D di Surya Institute mengembangkan metode pembelajaran matematika yang dinamakan metode Gasing (GAmpang, aSyIk, MenyenaNGkan). Pembelajaran Matematika Gasing dibuat secara bertahap, bertingkat dan berlanjut, dari konsep yang termudah hingga tersulit. Dengan cara ini siswa lebih mudah memahami matematika dan menemukan sendiri “AHA”-nya. Lewat metode Gasing ini diharapkan jutaan anak-anak Indonesia menjadi pandai berhitung dan tidak lagi takut dengan matematika.
Modul pertama ini disusun untuk memberi bimbingan pada orangtua atau pendidik bagaimana mengajar berhitung GASING yang meliputi BAKAL KUBAGI (penjumlahan atau penamBAhan, perKALian, pengurangan atau KUrang dan pemBAGIan). Pada Modul kedua nanti kita akan belajar GASING untuk materi PEDE (PEcahan dan DEsimal). Seorang yang mampu menguasai BAKAL KUBAGI PEDE akan mampu belajar matematika dengan sangat mudah.
Ucapan terima kasih tak lupa kami sampaikan kepada semua pihak yang telah membantu terselesaikannya modul ini. Akhirnya, saran dan masukan berkaitan dengan modul ini dapat disampaikan kepada penyusun melalui situs Kandel.
Tim Penyusun
Meaning GASING
Arti Metode GASING
Metode adalah cara (langkah demi langkah) untuk mencapai suatu hasil. GASING adalah GAmpang, aSIk, dan menyenaNGkan. Jadi Metode GASING berhitung adalah langkah demi langkah pembelajaran berhitung secara gampang, asik dan menyenangkan.
Pembelajaran Berhitung Gasing dibuat berurutan dari konsep yang termudah hingga tersulit sehingga siswa dapat dengan mudah memahami matematika dan menemukan sendiri “AHA”-nya.
Beberapa hal penting dalam metode Gasing
- Konkret - Abstrak
- Setiap materi pembelajaran Gasing selalu dimulai dengan sesuatu yang kongkret, sesuatu yang mudah divisualisasikan. Hal yang konkret ini membuat siswa lebih mudah mengerti. Tanpa bisa membayangkan lebih sulit bagi siswa untuk belajar suatu mata pelajaran.
- Misalnya seorang berkata cinq + vier = enea. Sulit bagi kita mengingat atau mengerti maksudnya. Tetapi kalau ia menunjukan jari 5 sambil berkata cinq (bahasa perancis), lalu menunjukan jari 4 sambil berkata vier (bahasa Jerman) dan menunjukan hasilnya adalah sembilan jari sambil berkata enea (bahasa yunani), maka siswa bisa mengerti lebih mudah.
- Setelah belajar kongkretnya, kita mengajarkan abstraknya, misalnya 5 + 4 = 9.
- Mencongak
- Perhitungan dengan metode Gasing sebagian besar dilakukan dengan mencongak. Mencongak bukan berarti menghafal, tetapi mengerti sehingga mampu melakukan perhitungan secara mencogak.
- Misalnya 19 x 3 sama dengan 1 puluhan x 3 satuan hasilnya adalah 3 puluhan, kemudian 9 satuan dikali 3 satuan hasilnya adalah 27 satuan yang merupakan 2 puluhan dan 7 satuan. Puluhannya digabung menjadi 3 + 2 = 5. Satuannya tetap 7. Sehingga hasilnya adalah 57.
- Agar lebih mudah menghitung secara mencongak maka perhitungan BAKAL KUBAGI selalu dimulai dari kiri ke kanan bukan dari kanan ke kiri seperti yang selama ini kita ajarkan.
- Bertahap
- Belajar Gasing adalah belajar setahap demi setahap. Misalnya untuk menguasai penjumlahan 5 digit dengan 5 digit tahapan yang perlu dilakukan adalah
- menguasai arti bilangan 1-5
- menguasai penjumlahan yang hasilnya 2 sampai 5
- menguasai arti bilangan 6 - 10
- menguasai penjumlahan yang hasilnya 6 sampai 10
- dst
- Bertingkat
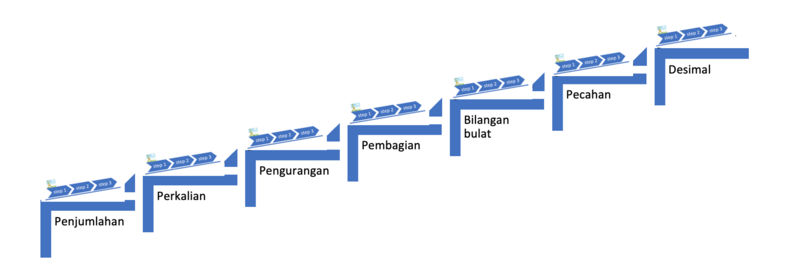
- Disamping bertahap, pembelajaran Gasing dibuat bertingkat. Tingkat pertama adalah Penjumlahan. Setelah menguasai penjumlahan, siswa baru bisa masuk ke perkalian. Kita tidak bisa mengajarkan perkalian tanpa lewat penjumlahan. Demikian juga pengurangan dapat dipelajari kalau sudah menguasai penjumlahan. Pembagian hanya dapat dikuasai setelah menguasai penjumlahan, perkalian dan pengurangan. Tingkatan-tingkatan yang akan kita pelajari dalam berhitung ini adalah
- Penjumlahan
- Perkalian
- Pengurangan
- Pembagian
- Bilangan bulat
- Pecahan
- Desimal
- Berlanjut
- Setelah menguasai Gasing berhitung, kita bisa lanjut ke soal cerita, soal teka-teki berhitung atau berbagai aplikasi seperti menghitung luas, kecepatan, perbandingan dsb.
- Titik Kritis
Dalam setiap tingkatan ada titik kritisnya. Titik kritis adalah keadaan dimana siswa sudah memahami dengan baik konsep-konsep dasar dari suatu tingkatan. Siswa yang telah mencapai titik kritis akan mampu menguasai konsep lanjutan dari tingkatan itu secara mudah.
Sebagai contoh : ‘’’titik kritis penjumlahan’’’ adalah penjumlahan yang hasilnya dibawah 20. Jadi untuk semua siswa yang sudah mampu menjumlahkan bilangan yang hasilnya kurang dari 20 sudah siap untuk melanjutkan pada konsep lanjutan penjumlahan seperti penjumlahan 2 digit, penjumlahan 3 digit dsb.
- Banyak Latihan
Siswa diberikan soal Latihan setelah siswa mampu mencongak. Jadi Latihan yang banyak adalah untuk meningkatkan kemampuan motorik siswa, bagaimana menuliskan apa yang ada diotak dalam bentuk tulisan tangan. Soal Latihan yang banyak juga untuk melatih ‘’’endurance’’’ anak. Mereka harus mengerjakan soal secara cepat misalnya 120 soal dalam waktu 3 menit, ini bermanfaat untuk melatih ‘’’konsentrasi’’’ mereka dan membiasakan bekerja secara cepat dan meningkatkan kerja otak. Latihan yang banyak dengan waktu yang cepat dapat meningkatkan kecerdasan (IQ) juga dan membuat siswa semakin mahir berhitung.
Perhatikan disini langkah demi langkah Gasing:
Kongkret → mencongak → berlatih dengan tulisan.
- Banyak memuji
Selama proses belajar pengajar harus banyak memuji anak untuk progress sekecil apapun juga. Pujian ini akan mendorong anak untuk belajar dan belajar lebih banyak. Pujian ini akan meningkatkan percaya diri siswa sehingga otak siswa akan bekerja lebih baik. Pujian akan membuat anak merasa dihargai dan ini membuat anak lebih mencintai matematika (ia merasa bahwa di ‘matematika’ lah ia dipuji dan dihargai).
Pujian bisa dilakukan secara dengan kata-kata seperti “kamu hebat sekali ya…”, “kamu makin lama makin hebat ya…” , “kamu ini luar biasa sekali”, “kamu akan jadi professor matematika yang sangat hebat…” dsb. Atau pujian ini juga bisa diberikan secara tertulis pada hasil kerja mereka. Seperti begitu mereka selesai menjawab 120 soal dalam 3 menit, kita tulis “wah luar biasa sekali Emon, kamu hebat sekali…” dsb..
- Mengajar dengan hati
Mengajar yang berhasil adalah ketika kita bisa menyamakan frekuensi irama berpikir otak kita dengan irama berpikir anak, kemudian sedikit demi sedikit kita bawa anak itu berfikir dengan frekuensi kita. Teknik ini sangat powerful. Untuk melakukan Teknik ini kita perlu mengajar dengan hati. Kita harus anggap siswa kita adalah makhluk Tuhan yang perlu kita latih sehingga pandai. Kita harus mengajar dengan hati yang tulus dan semangat ingin agar anak ini bisa pandai.
- Mengajar dengan musik/lagu
Indonesia adalah negara yang mencintai musik. Hampir tiap daerah punya lagu-lagu daerahnya masing-masing. Ketika kita mengajar matematika dengan lagu, siswa akan lebih senang dan lebih menangkap apa yang kita ajarkan. Lagu yang dikombinasikan dengan Gerakan dan matematika akan melatih otak kanan dan otak kiri secara bersama-sama dan ini akan menghasilkan efek yang luar biasa pada sang anak. Anak lebih cekatan, lebih cerdas dan lebih kreatif.
- Kecerdasan 6C
Dari penjelasan diatas dapat disimpulkan bahwa GASING itu mengembangkan kecerdasan 6C: Communication, Collaboration, Creativity, Compassion, Critical Thinking, Computational Logic
Gasing Counting: Whole Number
Titik Kritis Gasing dalam bilangan bulat ini adalah siswa mengerti konsep ambil/taruh gunung/lembah. Untuk mencapai titik kritis tersebut, Metode Gasing mengajarkan langkah demi langkah sebagai berikut:
Rahasia agar anak dapat menguasai operasi bilangan bulat adalah bakalkubagi-nya harus kuat.
Number line (Whole number concept)
Pada bagian ini kita akan belajar konsep bilangan bulat dengan memanfaatkan garis bilangan.
Ini adalah gambar garis bilangan.
- Garis bilangan adalah suatu garis yang didalamnya terdapat titik-titik dengan jarak sama antara dua titik yang berdekatan. Titik-titik ini diberi nama secara berurutan sesuai dengan pola tertentu.
- Pada gambar diatas antara satu bilangan dengan bilangan terdekatnya berjarak 1.
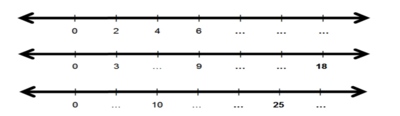
Dengan memperhatikan pola bilangan pada titik-titik dalam garis bilangan berikut ini, coba isi titik-titik yang kosong dengan bilangan bulat yang tepat.
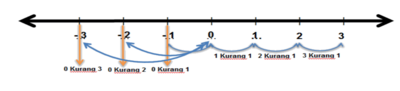
Perhatikan garis bilangan berikut:
- Mulai dari titik 3 melangkah ke kiri 1 skala tiba di titik 2. Titik 2 adalah titik tiga kurang satu"
- Mulai dari titik 3 melangkah ke kiri 2 skala tiba di titik 1. Titik 1 adalah titik tiga kurang dua"
- Mulai dari titik 3 melangkah ke kiri 3 skala tiba di titik 0. Titik 0 adalah titik tiga kurang tiga"
Selanjutnya,
- Dari 0 melangkah ke kiri 1 langkah tiba di titik yang disebut nol kurang satu
- Dari 0 melangkah ke kiri 2 langkah tiba di titik yang disebut nol kurang dua
- Dari 0 melangkah ke kiri 3 langkah tiba di titik yang disebut nol kurang tiga
Definisi
- 'nol kurang satu' disebut −1 (dibaca minus satu atau min satu atau negatif satu)
- 'nol kurang dua' disebut −2 (dibaca minus dua atau min dua atau negatif dua)
- 'nol kurang tiga' disebut −3 (dibaca minus tiga atau min tiga atau negatif tiga)
Bilangan dengan tanda -(minus) didepannya, disebut bilangan negatif.
Bilangan bulat dengan tanda -(minus) didepannya, disebut bilangan bulat negatif.
Gabungan bilangan bulat negatif, bilangan bulat positif dan 0 disebut bilangan bulat.
0 disebut bilangan bulat netral (bukan negatif bukan positif).
Addition and Subtraction using Number line
- Kita akan melakukan operasi bilangan bulat (penjumlahan dan pengurangan) dengan memanfaatkan garis bilangan.
- Beberapa hal yang perlu diperhatikan adalah:
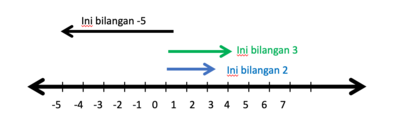
- Anak panah menunjukan bilangan
- Panjang anak panah menunjukan nilai bilangan tersebut
- Arah ke kanan untuk bilangan positif
- Arah ke kiri untuk bilangan negatif
- Operasi penjumlahan (+) artinya anak panah lama dilanjutkan anak panah baru
- Operasi pengurangan (-) artinya anak panah dilanjutkan pada arah berlawanan anak panah baru
Contoh:
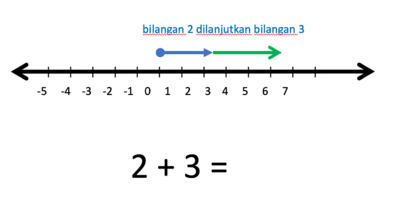
- a) 2 + 3 =....
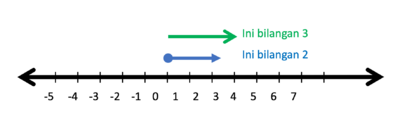
- Gambar bilangan 2 dan bilangan 3 berupa anak-anak panah yang dimulai dari titik 0.
- Operasi penjumlahan (+) artinya anak panah lama dilanjutkan anak panah baru
- Operasi pengurangan (-) artinya anak panah dilanjutkan pada arah berlawanan anak panah baru
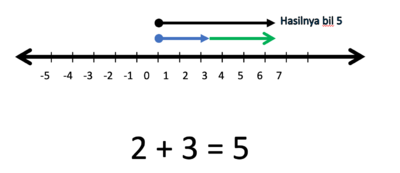
- Hasilnya adalah anak panah yang panjangnya 5 satuan, arahnya ke kanan.
- Jadi 2 + 3 = 5
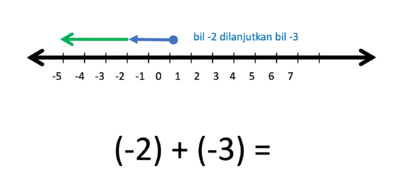
- b) (-2) + (-3) = ....
- Gambar bilangan -2 dan bilangan -3 berupa anak-anak panah yang dimulai dari titik 0.
- Operasi penjumlahan (+) artinya anak panah lama dilanjutkan anak panah baru
- Operasi pengurangan (-) artinya anak panah dilanjutkan pada arah berlawanan anak panah baru
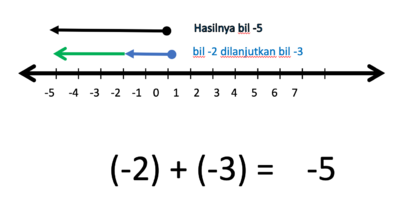
- Hasilnya adalah anak panah yang panjangnya 5 satuan, arahnya ke kiri.
- Jadi (-2) + (-3) = -5
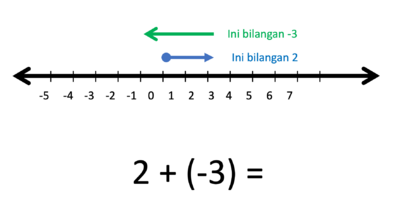
c) 2 + (-3) = ....
Gambar bilangan 2 dan bilangan -3 berupa anak-anak panah yang dimulai dari titik 0.
- Operasi penjumlahan (+) artinya anak panah lama dilanjutkan anak panah baru
- Operasi pengurangan (-) artinya anak panah dilanjutkan pada arah berlawanan anak panah baru
- Hasilnya adalah anak panah yang panjangnya 1 satuan, arahnya ke kiri.
- Jadi 2 + (-3) = -1
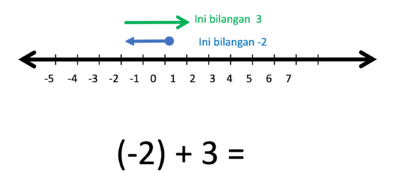
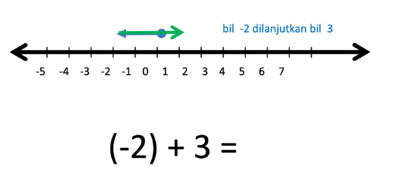
d) -2 + 3 = ....
Gambar bilangan -2 dan bilangan 3 berupa anak-anak panah yang dimulai dari titik 0.
- Operasi penjumlahan (+) artinya anak panah lama dilanjutkan anak panah baru
- Operasi pengurangan (-) artinya anak panah dilanjutkan pada arah berlawanan anak panah baru
- Hasilnya adalah anak panah yang panjangnya 1 satuan, arahnya ke kanan.
- Jadi -2 + 3 = 1
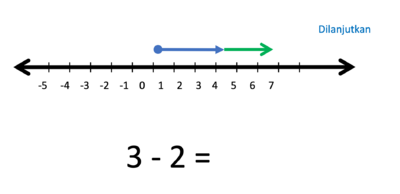
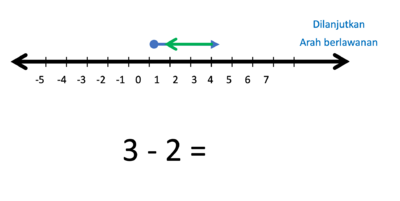
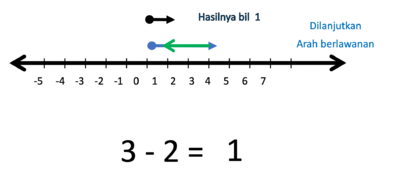
e) 3 - 2 = ....
Gambar bilangan 3 dan bilangan -2 berupa anak-anak panah yang dimulai dari titik 0.
- Operasi penjumlahan (+) artinya anak panah lama dilanjutkan anak panah baru
- Operasi pengurangan (-) artinya anak panah dilanjutkan pada arah berlawanan anak panah baru
- 3 kalau ditambahkan 2 hasilnya
- Tapi karena 3 dikurangi 2 maka anak panah 2 nya harus dibalik arah
- Hasilnya adalah anak panah yang panjangnya 1 satuan, arahnya ke kanan.
- Jadi 3 - 2 = 1
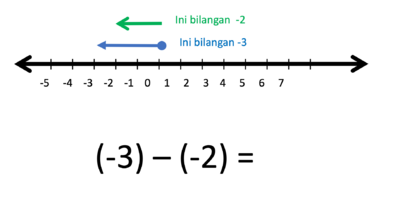
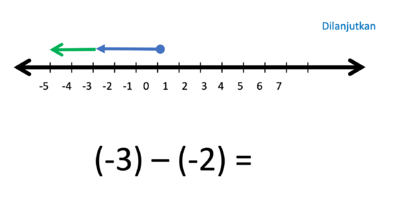
f) (-3) - (-2) = ....
Gambar bilangan -3 dan bilangan -2 berupa anak-anak panah yang dimulai dari titik 0.
- Operasi penjumlahan (+) artinya anak panah lama dilanjutkan anak panah baru
- Operasi pengurangan (-) artinya anak panah dilanjutkan pada arah berlawanan anak panah baru
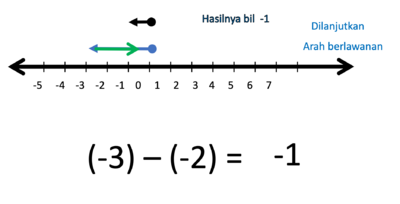
- -3 kalau ditambahkan -2 hasilnya
- Tapi karena -3 dikurangi -2 maka anak panah -2 nya harus dibalik arah
- Hasilnya adalah anak panah yang panjangnya 1 satuan, arahnya ke kiri.
- Jadi (-3) - (-2) = -1
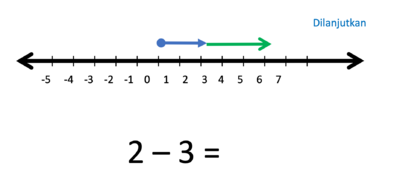
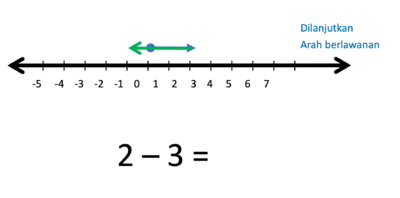
g) 2 - 3 = ....
Gambar bilangan 2 dan bilangan -3 berupa anak-anak panah yang dimulai dari titik 0.
- Operasi penjumlahan (+) artinya anak panah lama dilanjutkan anak panah baru
- Operasi pengurangan (-) artinya anak panah dilanjutkan pada arah berlawanan anak panah baru
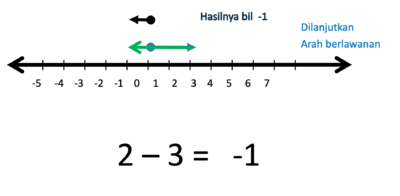
- 2 kalau ditambahkan 3 hasilnya
- Tapi karena 2 dikurangi 3 maka anak panah 3 nya harus dibalik arah
- Hasilnya adalah anak panah yang panjangnya 1 satuan, arahnya ke kiri.
- Jadi 2 - 3 = -1
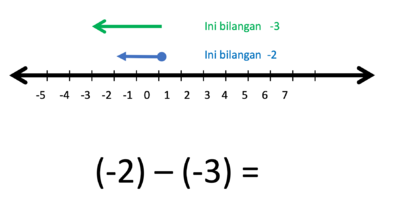
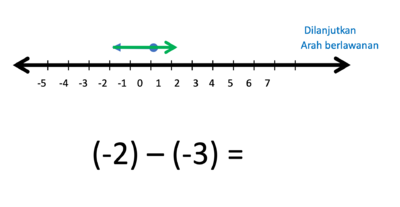
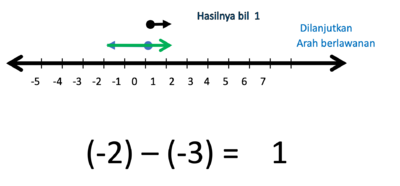
h) (-2) - (-3) = ....
Gambar bilangan -2 dan bilangan -3 berupa anak-anak panah yang dimulai dari titik 0.
- Operasi penjumlahan (+) artinya anak panah lama dilanjutkan anak panah baru
- Operasi pengurangan (-) artinya anak panah dilanjutkan pada arah berlawanan anak panah baru
- -2 kalau ditambahkan -3 hasilnya
- Tapi karena -2 dikurangi -3 maka anak panah -3 nya harus dibalik arah
- Hasilnya adalah anak panah yang panjangnya 1 satuan, arahnya ke kanan.
- Jadi (-2) - (-3) = 1
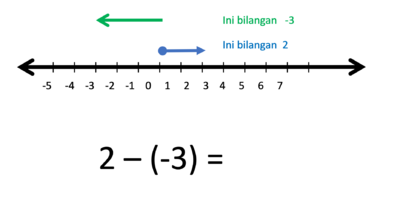
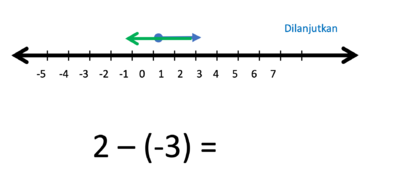
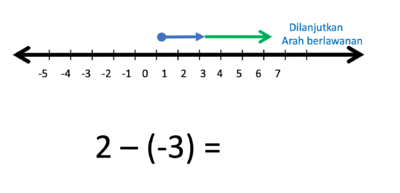
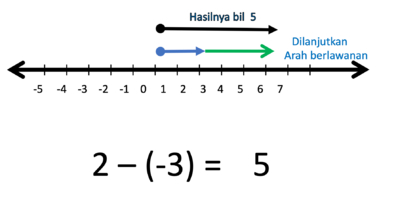
i) 2 - (-3) = ....
Gambar bilangan 2 dan bilangan -3 berupa anak-anak panah yang dimulai dari titik 0.
- Operasi penjumlahan (+) artinya anak panah lama dilanjutkan anak panah baru
- Operasi pengurangan (-) artinya anak panah dilanjutkan pada arah berlawanan anak panah baru
- 2 kalau ditambahkan -3 hasilnya
- Tapi karena 2 dikurangi -3 maka anak panah -3 nya harus dibalik arah
- Hasilnya adalah anak panah yang panjangnya 5 satuan, arahnya ke kanan.
- Jadi 2 - (-3) = 5
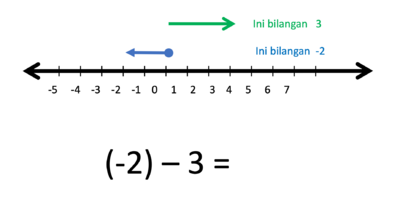
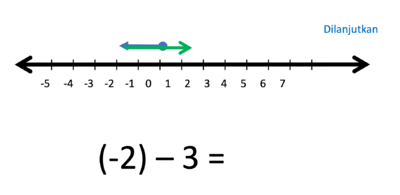
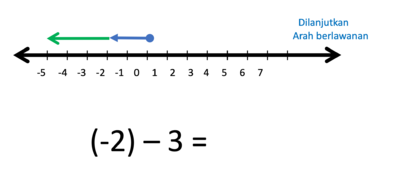
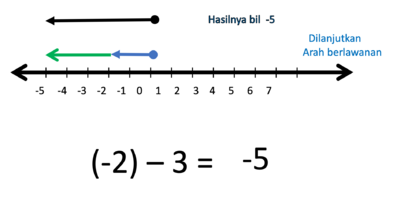
j) (-2) - 3 = ....
Gambar bilangan 2 dan bilangan -3 berupa anak-anak panah yang dimulai dari titik 0.
- Operasi penjumlahan (+) artinya anak panah lama dilanjutkan anak panah baru
- Operasi pengurangan (-) artinya anak panah dilanjutkan pada arah berlawanan anak panah baru
- (-2) kalau ditambahkan 3 hasilnya
- Tapi karena (-2) dikurangi 3 maka anak panah 3 nya harus dibalik arah
- Hasilnya adalah anak panah yang panjangnya 5 satuan, arahnya ke kiri.
- Jadi (-2) - 3 = -5
Benefit of Whole number
Misal kita sebut ketinggian di permukaan laut 0 meter, maka letak rumah, pohon dan benda-benda di atas permukaan laut dapat dinyatakan dengan suatu ketinggian 1 m, 2 m, dst. Bagaimana dengan yang di bawah permukaan laut?
Kita dapat mengatakan misalnya “kerang berada pada kedalaman 7 m di bawah permukaan air laut”. Akan tetapi ini terlalu panjang, dengan simbol bilangan negatif kita dapat mengatakan bahwa letak kerang adalah -7 m. Jadi, kita menggunakan bilangan negatif untuk yang di bawah permukaan air laut.
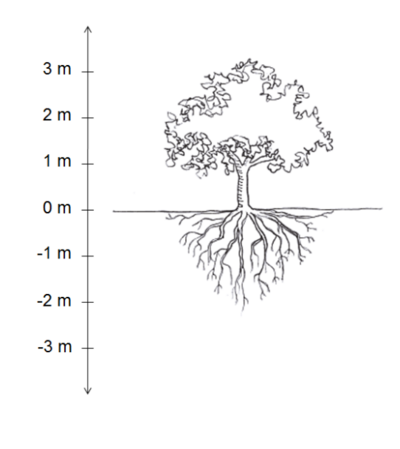
Ketinggian tepat pada permukaan tanah dianggap 0 m, di atas permukaan tanah menggunakan bilangan positif, dan di bawah permukaan tanah menggunakan bilangan negatif.
Pada Termometer, 0oC adalah suhu air membeku. Jika lebih panas dari suhu air membeku dianggap positif dan jika lebih dingin dari suhu air membeku dianggap negatif.
Valley and Hill concept
Pada bagian ini kita akan menggunakan konsep gunung dan lembah.
- Gunung melambangkan bilangan positif
- Nilai bilangan menyatakan banyak gunung
- Misal +3 menyatakan 1 gunung
- Lembah melambangkan bilangan negatif
- Nilai bilangan menyatakan banyak lembah
- Misal -1 menyatakan 1 lembah
- Tanah datar melambangkan 0
- 1 gunung + 1 lembah menjadi tanah datar yang nilainya sama dengan 0
- Tanah datar dapat dijadikan 1 gunung + 1 lembah, 2 gunung + 2 lembah, 50 gunung + 50 lembah dst.
Contoh:
Tiga gunung menyatakan bilangan 3
Tiga lembah menyatakan bilangan -3
Addition and subtraction
Pada bagian ini kita akan melakukan penjumlahan dan pengurangan bilangan bulat dengan memanfaatkan konsep gunung dan lembah.
Kita bagi operasi penjumlahan dan pengurangan ini dalam beberapa jenis.
- 1) Penjumlahan Sejenis
- a. 2 + 3 =....
- 2 diwakili oleh 2 gunung
- 3 diwakili oleh 3 gunung
- 2 gunung ditambahkan 3 gunung menjadi 5 gunung
- 2 + 3 = 5
- b. (-2) + (-3) = ....
- -2 diwakili oleh 2 lembah
- -3 diwakili oleh 3 lembah
- 2 lembah ditambahkan 3 lembah menjadi 5 lembah
- (-2) + (-3) = -5
- 2) Penjumlahan Berlainan Jenis
- a) 2 + (-3) =....
- 2 diwakili oleh 2 gunung
- -3 diwakili oleh 3 lembah
- Karena 2 gunung ditambah 2 lembah hasilnya tanah datar, maka
- 2 gunung ditambahkan 3 lembah hasilnya 1 lembah
- 2 + (-3) = -1
- b) (-2) + 3 =....
- -2 diwakili oleh 2 lembah
- 3 diwakili oleh 3 gunung
- Karena 2 lembah ditambahkan 2 gunung hasilnya tanah datar, maka
- 2 lembah ditambahkan 3 gunung hasilnya 1 gunung
- (-2) + 3 = 1.
- 3) Pengurangan Sejenis dan Cukup
- a) 3 – 2 =....
- 3 diwakili oleh 3 gunung
- 2 diwakili oleh 2 gunung
- 3 gunung diambil 2 gunung hasilnya adalah 1 gunung.
- 3 – 2 = 1.
- b) (-3) – (-2) = ....
- -3 diwakili oleh 3 lembah
- -2 diwakili oleh 2 lembah
- 3 lembah diambil 2 lembah hasilnya adalah 1 lembah.
- (-3) – (-2) = -1.
- 4) Pengurangan Sejenis dan Tidak Cukup
- a) 2 – 3 =....
- 2 diwakili oleh 2 gunung
- 3 diwakili oleh 3 gunung
- 2 gunung diambil 3 gunung.
- Ini tidak cukup
- Perlu membuat galian yang menghasilkan 1 gunung dan 1 lembah
- Total sekarang 3 gunung dan 1 lembah
- 3 gunung diambil, maka yang tersisa adalah 1 lembah.
- 2 – 3 = - 1.
- b) (-2) – (-3) = ....
- -2 diwakili oleh 2 lembah
- -3 diwakili oleh 3 lembah
- 2 lembah diambil 3 lembah.
- Ini tidak cukup
- Perlu membuat galian yang menghasilkan 1 gunung dan 1 lembah
- Total sekarang 3 lembah dan 1 gunung
- 3 lembah diambil, maka yang tersisa adalah 1 gunung.
- (-2) – (-3) = 1.
- 5) Pengurangan Berlainan Jenis
- a) 2 – (-3) =....
- -2 diwakili oleh 2 lembah
- -3 diwakili oleh 3 lembah
- 2 gunung diambil 3 lembah.
- Ini tidak bisa
- Perlu membuat galian yang menghasilkan 3 gunung dan 3 lembah
- Total sekarang 3 lembah dan 5 gunung
- 3 lembah diambil, maka yang tersisa adalah 5 gunung.
- 2 – (-3) = 5.
- b) (-2) – 3 = ....
- -2 diwakili oleh 2 lembah
- 3 diwakili oleh 3 gunung
- 2 lembah diambil 3 gunung.
- Ini tidak bisa
- Perlu membuat galian yang menghasilkan 3 gunung dan 3 lembah
- Total sekarang 5 lembah dan 3 gunung
- 3 gunung diambil, maka yang tersisa adalah 5 lembah.
- (-2) – 3 = - 5.
Cara cepat penjumlahan dan pengurangan
- Lingkari angka 3 dan angka +5.
- Disini kita punya 3 gunung dan 5 gunung
- Hasilnya 3 gunung + 5 gunung = 8 gunung.
- 3 + 5 = 8
- Lingkari angka 3 dan angka -5.
- Disini kita punya 3 gunung dan 5 lembah
- Disini lebih banyak lembah, sehingga hasilnya adalah lembah.
- Banyak lembah = bilangan lebih besar - bilangan lebih kecil = 5 - 3 = 2
- Hasilnya 2 lembah.
- 3 - 5 = -2
- Lingkari angka -3 dan angka +5.
- Disini kita punya 3 lembah dan 5 gunung.
- Disini lebih banyak gunung, sehingga hasilnya adalah gunung.
- Banyak lembah = bilangan lebih besar - bilangan lebih kecil = 5 - 3 = 2
- Hasilnya 2 gunung
- -3 + 5 = 2
- Lingkari angka -3 dan angka -5.
- Disini kita punya 3 lembah dan 5 lembah
- Hasilnya ada 3 lembah + 5 lembah = 8 lembah
- -3 - 5 = - 8
- Lingkari angka 123 dan angka +110.
- Disini kita punya 123 gunung dan 110 gunung
- Hasilnya ada 123 gunung + 110 gunung = 233 gunung.
- 123 + 110 = 233
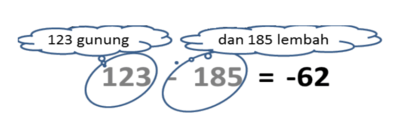
- Lingkari angka 123 dan angka -185.
- Disini kita punya 123 gunung dan 185 lembah.
- Disini lebih banyak lembah, sehingga hasilnya adalah lembah.
- Banyak lembah = bilangan lebih besar - bilangan lebih kecil = 185 - 123 = 62
- Hasilnya 62 lembah
- 123 - 185 = -62
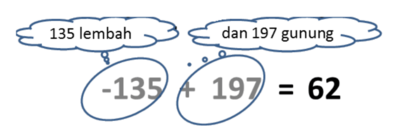
- Lingkari angka -135 dan angka +197.
- Disini kita punya 135 lembah dan 197 gunung.
- Disini lebih banyak gunung, sehingga hasilnya adalah gunung.
- Banyak gunung = bilangan lebih besar - bilangan lebih kecil = 197 - 135 = 62
- Hasilnya 62 gunung
- -135 + 197 = 62
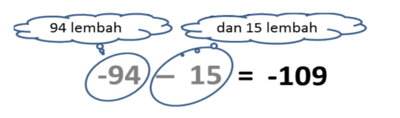
- Lingkari angka -94 dan angka -15.
- Disini kita punya 94 lembah dan 15 lembah
- Hasilnya ada 94 lembah + 15 lembah = 109 lembah
- -94 - 15 = - 109
Multiplication
Dalam bab ini kita akan melakukan perkalian bilangan bulat dengan memanfaatkan konsep gunung dan lembah.
Kita bahas 4 jenis perkalian
- a) 3 x 2 =....
- 3 x 2 artinya 3 kotak isi 2 gunung (dari definisi perkalian)
- Hasilnya adalah 2 gunung + 2 gunung + 2 gunung = 6 gunung
- 3 x 2 = 6
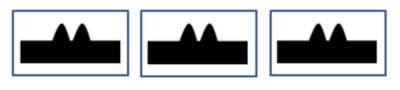
- b) 3 x (-2)=....
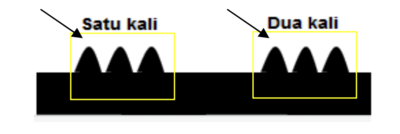
- 3 x (-2) artinya 3 kotak isi 2 lembah (dari definisi perkalian)
- Hasilnya adalah 2 lembah + 2 lembah + 2 lembah = 6 lembah
- 3 x (-2) = -6
- c) (-3) × 2 =....
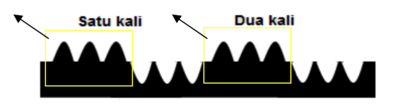
- 3 x 2 artinya ada 3 kotak isinya masing-masing 2 gunung
- (-3) x 2 artinya ada 3 anti kotak isinya masing-masing 2 gunung
- Disini kita belajar konsep anti kotak.
- Anti kotak mengubah gunung menjadi lembah
- Anti kotak mengubah lembah menjadi gunung
- Dalam anti kotak terdapat 2 gunung + 2 gunung + 2 gunung = 6 gunung
- Anti kotak akan merubah gunung jadi lembah
- Hasilnya adalah 6 lembah
- (-3) x 2 = -6
Cara lain
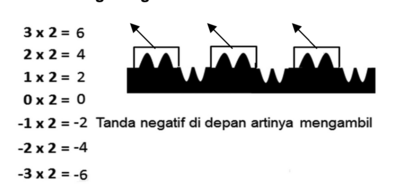
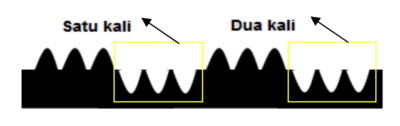
- Melihat Pola
Yang pertama dengan menggunakan alat peraga gunung dan lembah. Kita mulai dengan 3 x 2. Seperti disampaikan di atas, ini berarti kita MENARUH 2 gunung sebanyak 3 kali. Hasilnya 6 gunung, jadi 3 x 2 = 6. Lalu 2 x 2 artinya kita menaruh 2 gunung sebanyak 2 kali. Hasilnya 4 gunung, jadi 2 x 2 = 4. Lalu 1 x 2 artinya kita menaruh 2 gunung sekali. Hasilnya 2 gunung, jadi 1 x 2 = 2. Kemudian 0 x 2, artinya kita tidak melakukan apa-apa jadi nilainya 0. Sekarang – 1 x 2 artinya kita MENGAMBIL 2 gunung sekali, jadi seperti konkret untuk 0 – 2, terlihat hasilnya 2 lembah, jadi -1 x 2 = -2. Untuk -2 x 2 artinya kita mengambil 2 gunung sebanyak 2 kali, jadi tersisa 4 lembah, jadi -2 x 2 = -4. Untuk -3 x 2 artinya kita mengambil 2 gunung sebanyak 3 kali, jadi tersisa 6 lembah, jadi -3 x 2 = -6.
Cara Pola
[[[Image:Screen Shot 2022-02-11 at 15.26.41.png|200px]]
Mulai dari 3 x 2 = 6. Perhatikan hasil perkalian pada baris berikutnya berkurang 2. Sehingga kita peroleh hasil dari (-3) × 2 sama dengan -6.
Cara Komutatif
Selain menggunakan pola dari perkalian, kita juga dapat mendapatkan hasil perkalian tersebut dengan menggunakan sifat komutatif dari operasi perkalian. Jadi, sebagai contoh kita dapat memperoleh hasil (-3) × 2 dari 2 × (-3) = -6.
Itu yang dulu dipelajari waktu perkalian. Muncul pertanyaan, dari mana asal gunung tersebut? Harus ada yang menaruh. Dapat diartikan 3 x 2 sama dengan 3 kali menaruh 2 gunung: 2 gunung, 2 gunung, 2 gunung. Jadi, terdapat 6 gunung, sehingga 3 x 2 = 6. Untuk 3 x (-2) dapat diartikan 3 kali menaruh 2 lembah, jadi terdapat 6 lembah, sehingga dapat disimpulkan 3 x (-2) = -6. Untuk perkalian bilangan bulat, kalau bilangan di belakang simbol kali adalah positif artinya gunung dan kalau negatif artinya lembah. Sekarang kalau bilangan di depan simbol kali adalah positif artinya menaruh, kalau negatif artinya mengambil. Ini akan kita lihat pada jenis perkalian berikutnya.
d) (-3) × (-2) = ....
Cara Konkret Gunung dan Lembah Dengan menggunakan konkret gunung dan lembah, -3 x -2 artinya mengambil 2 lembah sebanyak 3 kali, sehingga tersisa 6 gunung. Jadi, -3 x -2 = 6.
Cara Pola
Dengan menggunakan pola perkalian kita juga dapat memperoleh hasil dari perkalian tersebut:
Sehingga kita peroleh hasil dari (-3) × (-2) sama dengan 6.
Dengan demikian dapat disimpulkan, bahwa:
Ini tidak perlu dihafal, siswa dapat membayangkan konkret gunung dan lembahnya.
Division
7. Operasi Pembagian Operasi pembagian pada bilangan bulat dapat dikaitkan dengan operasi perkalian bilangan bulat.
Contoh:
a) 6÷3=...dapatdiarahkandengan...×3=6 2 x 3 = 6 (dua kali taruh 3 gunung hasilnya 6 gunung) 2 = 6 ÷ 3 (kedua sisi dibagi 3) Jadi, 6 ÷ 3 arti konkretnya berapa kali taruh/ambil 3 gunung untuk mendapatkan 6 gunung.
Jawabannya adalah 2 kali taruh, jadi 6 ÷ 3 = +2 = 2.
b) (-6) ÷ (-3) = ... dapat diarahkan dengan ... × (-3) = (-6) 2 x -3 = -6 (dua kali taruh 3 lembah hasilnya 6 lembah) 2 = -6 ÷ -3 (kedua sisi dibagi -3) Jadi, -6 ÷ -3 arti konkretnya berapa kali taruh/ambil 3 lembah untuk mendapatkan 6 lembah.
Jawabannya adalah 2 kali taruh, jadi (-6) ÷ (-3) = +2 = 2.
c) (-6)÷3=...dapatdiarahkandengan...×3=(-6) -2 x 3 = -6 (dua kali ambil 3 gunung hasilnya 6 lembah) -2 = -6 ÷ 3 (kedua sisi dibagi 3) Jadi, -6 ÷ 3 arti konkretnya berapa kali taruh/ambil 3 gunung untuk mendapatkan 6 lembah.
Jawabannya adalah 2 kali ambil, jadi (-6) ÷ 3 = -2.
d) 6÷(-3)=...dapatdiarahkandengan...×(-3)=6 -2 x -3 = 6 (dua kali ambil 3 lembah hasilnya 6 gunung) -2 = 6 ÷ -3 (kedua sisi dibagi -3) Jadi, 6 ÷ -3 arti konkretnya berapa kali taruh/ambil 3 lembah untuk mendapatkan 6 gunung.
Jawabannya adalah 2 kali ambil, jadi 6 ÷ (-3) = -2.
Ingat taruh tandanya positif dan ambil tandanya negatif. Juga, Menaruh gunung, hasilnya gunung. Menaruh lembah hasilnya lembah. Mengambil gunung, menghasilkan lembah. Mengambil lembah, hasilnya adalah gunung.
Kesimpulan: