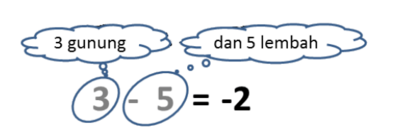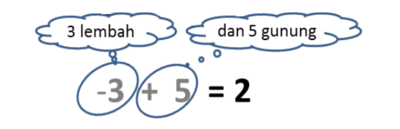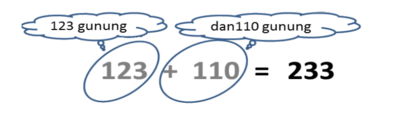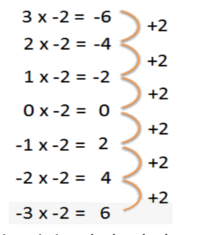GABER Bilangan Bulat
Gasing Berhitung: Bilangan Bulat
Mengapa kita harus belajar bilangan bulat?
Aplikasi bilangan bulat sering kita jumpai dalam kehidupan sehari-hari. Ada banyak fenomena/peristiwa yang terjadi dalam kehidupan sehari-hari yang berkiatan dengan konsep bilangan bulat, diantaranya adalah :
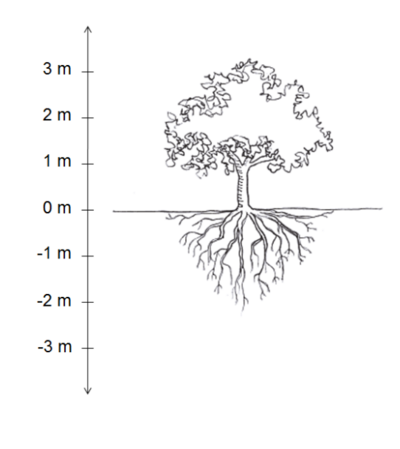
1. Ketinggian dan Kedalaman Misal kita sebut ketinggian di permukaan laut 0 meter, maka letak rumah, pohon dan benda-benda di atas permukaan laut dapat dinyatakan dengan suatu ketinggian 1 m, 2 m, dst. Bagaimana dengan yang di bawah permukaan laut?
Kita dapat mengatakan misalnya “kerang berada pada kedalaman 7 m di bawah permukaan air laut”. Akan tetapi ini terlalu panjang, dengan simbol bilangan negatif kita dapat mengatakan bahwa letak kerang adalah -7 m. Jadi, kita menggunakan bilangan negatif untuk benda yang berada di bawah permukaan air laut.
Ketinggian tepat pada permukaan tanah dianggap 0 m, di atas permukaan tanah menggunakan bilangan positif, dan di bawah permukaan tanah menggunakan bilangan negatif.
2. Suhu/Temperatur:
Pada Termometer, 0oC adalah suhu es mencair. Jika lebih panas dari suhu es mencair maka suhunya dinyatakan dengan bilangan positif dan jika lebih dingin dari suhu es mencair dinyatakan dengan bilangan negatif.
Apakah yang dimaksud dengan bilangan postif dan negatif??? Dapatkan jawabannya dalam uraian berikut ini.
Titik Kritis Gasing Bilangan Bulat
Titik Kritis Gasing dalam bilangan bulat ini adalah siswa mengerti konsep ambil/gabung gunung/lembah. Untuk mencapai titik kritis tersebut, Metode Gasing mengajarkan langkah demi langkah sebagai berikut:
Rahasia agar anak dapat menguasai operasi bilangan bulat adalah bakalkubagi(tambah, kali, kurang dan bagi)-nya harus kuat.
Konsep Bilangan Bulat dengan Garis Bilangan
Pada bagian ini kita akan belajar konsep bilangan bulat dengan memanfaatkan Garis Bilangan.
Ini adalah gambar garis bilangan.
- Garis bilangan adalah suatu garis yang didalamnya terdapat titik-titik dengan jarak sama antara dua titik yang berdekatan. Titik-titik ini diberi nama secara berurutan sesuai dengan pola tertentu.
- Pada gambar diatas antara satu bilangan dengan bilangan terdekatnya berjarak 1.
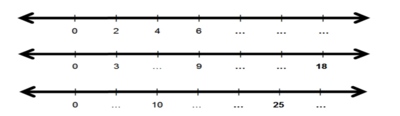
Dengan memperhatikan pola bilangan pada titik-titik dalam garis bilangan berikut ini, coba isi titik-titik yang kosong dengan bilangan bulat yang tepat.
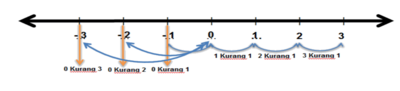
Perhatikan garis bilangan berikut:
- Mulai dari titik 3 melangkah ke kiri 1 skala tiba di titik 2. Titik 2 adalah titik tiga kurang satu"
- Mulai dari titik 3 melangkah ke kiri 2 skala tiba di titik 1. Titik 1 adalah titik tiga kurang dua"
- Mulai dari titik 3 melangkah ke kiri 3 skala tiba di titik 0. Titik 0 adalah titik tiga kurang tiga"
Selanjutnya,
- Dari 0 melangkah ke kiri 1 langkah tiba di titik yang disebut nol kurang satu
- Dari 0 melangkah ke kiri 2 langkah tiba di titik yang disebut nol kurang dua
- Dari 0 melangkah ke kiri 3 langkah tiba di titik yang disebut nol kurang tiga
Definisi
- 'nol kurang satu' disebut −1 (dibaca minus satu atau min satu atau negatif satu)
- 'nol kurang dua' disebut −2 (dibaca minus dua atau min dua atau negatif dua)
- 'nol kurang tiga' disebut −3 (dibaca minus tiga atau min tiga atau negatif tiga)
Bilangan dengan tanda -(minus) didepannya, disebut bilangan negatif.
Bilangan bulat dengan tanda -(minus) didepannya, disebut bilangan bulat negatif.
Gabungan bilangan bulat negatif, bilangan bulat positif dan 0 disebut bilangan bulat.
0 disebut bilangan bulat netral (bukan negatif bukan positif).
Operasi Bilangan Bulat (Penjumlahan dan Pengurangan) dengan menggunakan Garis Bilangan
- Kita akan melakukan operasi bilangan bulat (penjumlahan dan pengurangan) dengan memanfaatkan garis bilangan.
- Beberapa hal yang perlu diperhatikan adalah:
- Anak panah menunjukan bilangan
- Panjang anak panah menunjukan nilai bilangan tersebut
- Arah ke kanan untuk bilangan positif
- Arah ke kiri untuk bilangan negatif
- Operasi penjumlahan (+) artinya anak panah pertama dilanjutkan anak panah berikutnya
- Operasi pengurangan (-) artinya anak panah pertama dilanjutkan pada arah berlawanan anak panah berikutnya.
Contoh:
- a) 2 + 3 =....
- Gambar bilangan 2 dan bilangan 3 berupa anak-anak panah yang dimulai dari titik 0.
- Operasi penjumlahan (+) artinya anak panah pertama dilanjutkan anak panah berikutnya
- Hasilnya adalah anak panah yang panjangnya 5 satuan, arahnya ke kanan yang bernilai 5 (positif 5).
- Jadi 2 + 3 = 5
- b) (-2) + (-3) = ....
- Gambar bilangan -2 dan bilangan -3 berupa anak-anak panah yang dimulai dari titik 0.
- Operasi penjumlahan (+) artinya anak panah pertama dilanjutkan anak panah berikutnya
- Hasilnya adalah anak panah yang panjangnya 5 satuan, arahnya ke kiri yang bernilai -5.
- Jadi (-2) + (-3) = -5
c) 2 + (-3) = ....
Gambar bilangan 2 dan bilangan -3 berupa anak-anak panah yang dimulai dari titik 0.
- Operasi penjumlahan (+) artinya anak panah pertama dilanjutkan anak panah berikutnya
- Hasilnya adalah anak panah yang panjangnya 1 satuan, arahnya ke kiri yang bernilai -1.
- Jadi 2 + (-3) = -1
d) -2 + 3 = ....
Gambar bilangan -2 dan bilangan 3 berupa anak-anak panah yang dimulai dari titik 0.
- Operasi penjumlahan (+) artinya anak panah pertama dilanjutkan anak panah berikutnya
- Hasilnya adalah anak panah yang panjangnya 1 satuan, arahnya ke kanan yang bernilai 1.
- Jadi -2 + 3 = 1
e) 3 - 2 = ....
Gambar bilangan 3 dan bilangan 2 berupa anak-anak panah yang dimulai dari titik 0.
- Operasi pengurangan (-) artinya anak panah pertama dilanjutkan dengan anak panah berikutnya yang arahnya berlawanan.
- 3 kalau ditambahkan 2 hasilnya
- Tapi karena 3 dikurangi 2 maka anak panah 2 nya harus dibalik arah
- Hasilnya adalah anak panah yang panjangnya 1 satuan, arahnya ke kanan yang bernilai 1.
- Jadi 3 - 2 = 1
f) (-3) - (-2) = ....
Gambar bilangan -3 dan bilangan -2 berupa anak-anak panah yang dimulai dari titik 0.
- Operasi pengurangan (-) artinya anak panah pertama dilanjutkan dengan anak panah berikutnya yang arahnya berlawanan.
- -3 kalau ditambahkan -2 hasilnya
- Tapi karena -3 dikurangi -2 maka anak panah -2 nya harus dibalik arah
- Hasilnya adalah anak panah yang panjangnya 1 satuan, arahnya ke kiri yang bernilai -1.
- Jadi (-3) - (-2) = -1
g) 2 - 3 = ....
Gambar bilangan 2 dan bilangan 3 berupa anak-anak panah yang dimulai dari titik 0.
- Operasi pengurangan (-) artinya anak panah pertama dilanjutkan dengan anak panah berikutnya yang arahnya berlawanan.
- 2 kalau ditambahkan 3 hasilnya
- Tapi karena 2 dikurangi 3 maka anak panah 3 nya harus dibalik arah
- Hasilnya adalah anak panah yang panjangnya 1 satuan, arahnya ke kiri yang bernilai -1.
- Jadi 2 - 3 = -1
h) (-2) - (-3) = ....
Gambar bilangan -2 dan bilangan -3 berupa anak-anak panah yang dimulai dari titik 0.
- Operasi pengurangan (-) artinya anak panah pertama dilanjutkan dengan anak panah berikutnya yang arahnya berlawanan.
- -2 kalau ditambahkan -3 hasilnya
- Tapi karena -2 dikurangi -3 maka anak panah -3 nya harus dibalik arah
- Hasilnya adalah anak panah yang panjangnya 1 satuan, arahnya ke kanan yang bernilai 1.
- Jadi (-2) - (-3) = 1
i) 2 - (-3) = ....
Gambar bilangan 2 dan bilangan -3 berupa anak-anak panah yang dimulai dari titik 0.
- Operasi pengurangan (-) artinya anak panah pertama dilanjutkan dengan anak panah berikutnya yang arahnya berlawanan.
- 2 kalau ditambahkan -3 hasilnya
- Tapi karena 2 dikurangi -3 maka anak panah -3 nya harus dibalik arah
- Hasilnya adalah anak panah yang panjangnya 5 satuan, arahnya ke kanan yang bernilai 5.
- Jadi 2 - (-3) = 5
j) (-2) - 3 = ....
Gambar bilangan -2 dan bilangan 3 berupa anak-anak panah yang dimulai dari titik 0.
- Operasi pengurangan (-) artinya anak panah pertama dilanjutkan dengan anak panah berikutnya yang arahnya berlawanan.
- (-2) kalau ditambahkan 3 hasilnya
- Tapi karena (-2) dikurangi 3 maka anak panah 3 nya harus dibalik arah
- Hasilnya adalah anak panah yang panjangnya 5 satuan, arahnya ke kiri yang nilainya -5.
- Jadi (-2) - 3 = -5
Konsep Gunung dan Lembah
Pada bagian ini kita akan menggunakan konsep Gunung dan Lembah.
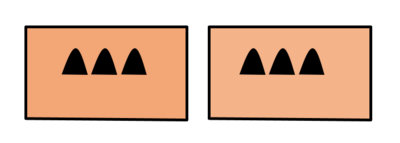
- Gunung melambangkan bilangan positif
- Nilai bilangan menyatakan banyak gunung
- Misal 1 gunung melambangkan +1 atau 1.
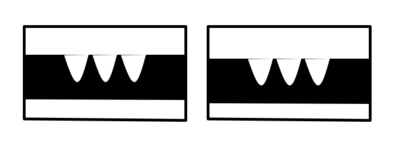
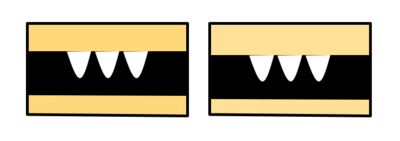
- Lembah melambangkan bilangan negatif
- Nilai bilangan menyatakan banyak lembah
- Misal 1 lembah melambangkan bilangan -1
- Tanah datar melambangkan 0
- 1 gunung + 1 lembah menjadi tanah datar yang nilainya sama dengan 0
- Tanah datar dapat dibentuk dari 1 gunung + 1 lembah, 2 gunung + 2 lembah, 50 gunung + 50 lembah dst.
Contoh:
Tiga gunung menyatakan bilangan 3
Tiga lembah menyatakan bilangan -3
Penjumlahan dan Pengurangan
Pada bagian ini kita akan melakukan penjumlahan dan pengurangan bilangan bulat dengan memanfaatkan konsep Gunung dan Lembah.
Kita bagi operasi penjumlahan dan pengurangan ini dalam beberapa jenis.
- 1) Penjumlahan Sejenis
Disini kita akan menjumlahkan bilangan positif dengan bilangan positif atau bilangan negatif dengan bilangan negatif.
- a. 2 + 3 =....
- 2 diwakili oleh 2 gunung
- 3 diwakili oleh 3 gunung
- 2 gunung ditambahkan 3 gunung menjadi 5 gunung
- 2 + 3 = 5
- b. (-2) + (-3) = ....
- -2 diwakili oleh 2 lembah
- -3 diwakili oleh 3 lembah
- 2 lembah ditambahkan 3 lembah menjadi 5 lembah
- (-2) + (-3) = -5
- 2) Penjumlahan Berlainan Jenis
Disini kita akan melakukan penjumlahan bilangan negatif dan bilangan positif.
- a) 2 + (-3) =....
- 2 diwakili oleh 2 gunung
- -3 diwakili oleh 3 lembah
- Karena 2 gunung ditambah 2 lembah hasilnya tanah datar, maka
- 2 gunung ditambahkan 3 lembah hasilnya 1 lembah
- 2 + (-3) = -1
- b) (-2) + 3 =....
- -2 diwakili oleh 2 lembah
- 3 diwakili oleh 3 gunung
- Karena 2 lembah ditambahkan 2 gunung hasilnya tanah datar, maka
- 2 lembah ditambahkan 3 gunung hasilnya 1 gunung
- (-2) + 3 = 1.
- 3) Pengurangan Sejenis dan Cukup
Disini kita melakukan operasi pengurangan, dan bilangan yang dikurangi lebih besar dari bilangan pengurang.
- a) 3 – 2 =....
- 3 diwakili oleh 3 gunung
- 2 diwakili oleh 2 gunung
- 3 gunung diambil 2 gunung hasilnya adalah 1 gunung.
- 3 – 2 = 1.
- b) (-3) – (-2) = ....
- -3 diwakili oleh 3 lembah
- -2 diwakili oleh 2 lembah
- 3 lembah diambil 2 lembah hasilnya adalah 1 lembah.
- (-3) – (-2) = -1.
- 4) Pengurangan Sejenis dan Tidak Cukup
Disini kita melakukan operasi pengurangan, dan bilangan yang dikurangi lebih kecil dari bilangan pengurang.
- a) 2 – 3 =....
- 2 diwakili oleh 2 gunung
- 3 diwakili oleh 3 gunung
- 2 gunung diambil 3 gunung.
- Ini tidak cukup
- Perlu membuat galian yang menghasilkan 1 gunung dan 1 lembah
- Total sekarang 3 gunung dan 1 lembah
- 3 gunung diambil, maka yang tersisa adalah 1 lembah.
- 2 – 3 = - 1.
- b) (-2) – (-3) = ....
- -2 diwakili oleh 2 lembah
- -3 diwakili oleh 3 lembah
- 2 lembah diambil 3 lembah.
- Ini tidak cukup
- Perlu membuat galian yang menghasilkan 1 gunung dan 1 lembah
- Total sekarang 3 lembah dan 1 gunung
- 3 lembah diambil, maka yang tersisa adalah 1 gunung.
- (-2) – (-3) = 1.
- 5) Pengurangan Berlainan Jenis
Disini kita akan melakukan operasi pengurangan bilangan positif dan negatif atau sebaliknya.
- a) 2 – (-3) =....
- -2 diwakili oleh 2 lembah
- -3 diwakili oleh 3 lembah
- 2 gunung diambil 3 lembah.
- Ini tidak bisa
- Perlu membuat galian yang menghasilkan 3 gunung dan 3 lembah
- Total sekarang 3 lembah dan 5 gunung
- 3 lembah diambil, maka yang tersisa adalah 5 gunung.
- 2 – (-3) = 5.
- b) (-2) – 3 = ....
- -2 diwakili oleh 2 lembah
- 3 diwakili oleh 3 gunung
- 2 lembah diambil 3 gunung.
- Ini tidak bisa
- Perlu membuat galian yang menghasilkan 3 gunung dan 3 lembah
- Total sekarang 5 lembah dan 3 gunung
- 3 gunung diambil, maka yang tersisa adalah 5 lembah.
- (-2) – 3 = - 5.
Cara cepat penjumlahan dan pengurangan
a) Soal memakai tanda kurung
- Penjumlahan
i) (-5) + 9 = Bayangkan ada 5 lembah dan 9 gunung. Yang lebih banyak adalah gunung. Hasilnya adalah berupa gunung. Banyaknya gunung 9 - 5 = 4. Jadi (-5) + 9 = 4
ii) (-5) + (-9) = Bayangkan ada 5 lembah dan 9 lembah. Disini lembahnya akan bertambah banyak. Hasilnya adalah berupa lembah Banyaknya lembah 5 + 9 = 14. Jadi (-5) + (-9) = -14
iii) 5 + (-9) = Bayangkan ada 5 gunung dan 9 lembah. Yang lebih banyak adalah lembah. Hasilnya adalah berupa lembah. Banyaknya lembah 9 - 5 = 4. Jadi 5 + (-9) = -4
- Pengurangan
iv) (-5) - 9 = Bayangkan ada 5 lembah hendak diambil 9 gunung. Yang kita lakukan adalah buat 9 gunung dan 9 lembah. 9 Gunungnya diambil. Tersisa 5 lembah dan 9 lembah Banyaknya lembah 5 + 9 = 14. Jadi (-5) - 9 = 14
v) (-5) -(- 9) = Bayangkan ada 5 lembah hendak diambil 9 lembah. Yang kita lakukan adalah buat 4 gunung dan 4 lembah. 9 lembahnya diambil. Tersisa 4 Gunung Jadi (-5) - (-9) = 4
vi) (-9) -(- 5) = Bayangkan ada 9 lembah hendak diambil 5 lembah. Hasilnya 4 lembah. Jadi (-9) - (-5) = -4
b) Soal tidak memakai tanda kurung
- Lingkari angka 3 dan angka +5.
- Disini kita punya 3 gunung dan 5 gunung
- Hasilnya 3 gunung + 5 gunung = 8 gunung.
- 3 + 5 = 8
- Lingkari angka 3 dan angka -5.
- Disini kita punya 3 gunung dan 5 lembah
- Disini lebih banyak lembah, sehingga hasilnya adalah lembah.
- Banyak lembah = bilangan lebih besar - bilangan lebih kecil = 5 - 3 = 2
- Hasilnya 2 lembah.
- 3 - 5 = -2
- Mengapa 3 dikurang 5 dapat dianggap sebagai 3 ditambah (-5)?
Perhatikan berikut ini:
- 3 - 5 = 3 gunung kurang 5 gunung
- = 3 gunung tambah 5 gunung tambah 5 lembah kurang 5 gunung
- = 3 gunung tambah 5 lembah
- = 3 + (-5)
- Lingkari angka -3 dan angka +5.
- Disini kita punya 3 lembah dan 5 gunung.
- Disini lebih banyak gunung, sehingga hasilnya adalah gunung.
- Banyak lembah = bilangan lebih besar - bilangan lebih kecil = 5 - 3 = 2
- Hasilnya 2 gunung
- -3 + 5 = 2
- Lingkari angka -3 dan angka -5.
- Disini kita punya 3 lembah dan 5 lembah
- Hasilnya ada 3 lembah + 5 lembah = 8 lembah
- -3 - 5 = - 8
- Lingkari angka 123 dan angka +110.
- Disini kita punya 123 gunung dan 110 gunung
- Hasilnya ada 123 gunung + 110 gunung = 233 gunung.
- 123 + 110 = 233
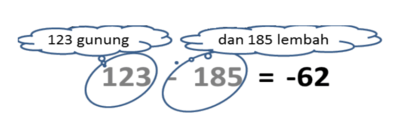
- Lingkari angka 123 dan angka -185.
- Disini kita punya 123 gunung dan 185 lembah.
- Disini lebih banyak lembah, sehingga hasilnya adalah lembah.
- Banyak lembah = bilangan lebih besar - bilangan lebih kecil = 185 - 123 = 62
- Hasilnya 62 lembah
- 123 - 185 = -62
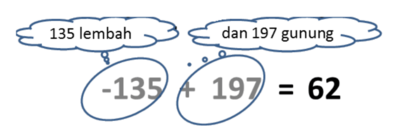
- Lingkari angka -135 dan angka +197.
- Disini kita punya 135 lembah dan 197 gunung.
- Disini lebih banyak gunung, sehingga hasilnya adalah gunung.
- Banyak gunung = bilangan lebih besar - bilangan lebih kecil = 197 - 135 = 62
- Hasilnya 62 gunung
- -135 + 197 = 62
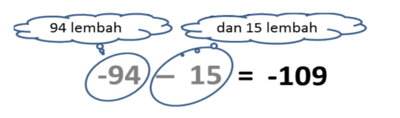
- Lingkari angka -94 dan angka -15.
- Disini kita punya 94 lembah dan 15 lembah
- Hasilnya ada 94 lembah + 15 lembah = 109 lembah
- -94 - 15 = - 109
Aktivitas 1 berlatih penjumlahan dan pengurangan bilangan bulat
- Tujuan: Siswa menuliskan dengan cepat hasil penjumlahan dan pengurangan bilangan bulat
- Siswa mengerjakan dari buku Pengurangan dan Pembagian (buku 3) Latihan 18a-c
Perkalian Bilangan Bulat
Dalam bab ini kita akan melakukan perkalian bilangan bulat dengan memanfaatkan konsep Gunung dan Lembah.
Kita bahas 4 jenis perkalian
- a) 3 x 2 =....
- 3 x 2 artinya 3 kotak isi 2 gunung (dari definisi perkalian)
- Hasilnya adalah 2 gunung + 2 gunung + 2 gunung = 6 gunung
- 3 x 2 = 6
- b) 3 x (-2)=....
- 3 x (-2) artinya 3 kotak isi 2 lembah (dari definisi perkalian)
- Hasilnya adalah 2 lembah + 2 lembah + 2 lembah = 6 lembah
- 3 x (-2) = -6
- c) (-3) × 2 =....
- 3 x 2 artinya ada 3 kotak isinya masing-masing 2 gunung
- (-3) x 2 artinya ada 3 anti kotak isinya masing-masing 2 gunung
- Disini kita belajar konsep anti kotak.
- Anti kotak mengubah gunung menjadi lembah dan sebaliknya mengubah lembah menjadi gunung
- Dalam anti kotak terdapat 2 gunung + 2 gunung + 2 gunung = 6 gunung
- Anti kotak akan mengubah gunung jadi lembah
- Hasilnya adalah 6 lembah
- (-3) x 2 = -6
Cara lain (bukan cara Gasing)
- Sifat komutatif perkalian
- karena 2 x 3 = 3 x 2
- maka 2 x (-3) = -3 x 2
- Melihat Pola (bukan cara Gasing)
- Error creating thumbnail: Unable to save thumbnail to destination
- Mulai dari 3 x 2 = 6.
- Perhatikan hasil perkalian pada baris berikutnya berkurang 2.
- Dengan demikian kita bisa peroleh (-3) × 2 = -6.
d) (-3) × (-2) = ....
- 3 x (-2) artinya ada 3 kotak isinya masing-masing 2 lembah
- (-3) x (-2) artinya ada 3 anti kotak isinya masing-masing 2 lembah
- Disini kita belajar konsep anti kotak.
- Anti kotak mengubah gunung menjadi lembah dan sebaliknya mengubah lembah menjadi gunung
- Dalam anti kotak terdapat 2 lembah + 2 lembah + 2 lembah = 6 lembah
- Anti kotak akan merubah lembah jadi gunung
- Hasilnya adalah 6 gunung
- (-3) x (-2) = 6
Cara lain
- Melihat pola (bukan cara Gasing)
- Mulai dari 3 x (-2) = -6.
- Perhatikan hasil perkalian pada baris berikutnya bertambah 2.
- Dengan demikian kita bisa peroleh (-3) × (-2) = 6.
Kesimpulan
- Untuk perkalian bilangan bulat berlaku
Aktivitas 2 berlatih perkalian bilangan bulat
- Tujuan: Siswa menuliskan dengan cepat hasil perkalian bilangan bulat
- Siswa mengerjakan dari buku Pengurangan dan Pembagian (buku 3) Latihan 19
Pembagian Bilangan Bulat
Kita akan melakukan operasi pembagian dengan menggunakan konsep gunung dan lembah.
Contoh:
- a) 6 ÷ 2 =...
- Artinya 6 gunung hendak dibagikan ke dalam 2 kotak, masing-masing kotak menerima berapa gunung?
- Jawabnya adalah 3 gunung
- jadi 6 : 2 = 3
- b) (-6) ÷ 2 =...
- Artinya 6 lembah hendak dibagikan ke dalam 2 kotak, masing-masing kotak menerima berapa lembah?
- Jawabnya adalah 3 lembah
- jadi (-6) : 2 = -3
- c) 6 ÷ (-2) =...
- Artinya 6 gunung hendak dibagikan ke dalam 2 anti kotak, masing-masing anti kotak menerima berapa gunung?
- Jawabnya adalah 3 gunung
- Namun anti kotak akan mengubah gunung jadi lembah. Sehingga hasilnya 3 lembah
- jadi 6 : (-2) = -3
- d) -6 ÷ (-2) =...
- Artinya 6 lembah hendak dibagikan ke dalam 2 anti kotak, masing-masing anti kotak menerima berapa lembah?
- Jawabnya adalah 3 lembah
- Namun anti kotak akan mengubah lembah jadi gunung. Sehingga hasilnya 3 gunung
- jadi -6 : (-2) = 3
Aktivitas 2 berlatih pembagian bilangan bulat
- Tujuan: Siswa menuliskan dengan cepat hasil pembagian bilangan bulat
- Siswa mengerjakan dari buku Pengurangan dan Pembagian (buku 3) Latihan 20