读《哥德尔、艾舍尔、巴赫：集异璧之大成》有感

Final Project

对人类的认知过程的认知 ——读《哥德尔、艾舍尔、巴赫：集异璧之大成》有感

本书目录

• 【一】形式系统
• 【二】讨论形式系统的意义
• 【三】递归可枚举集、递归集概念
• 【四】维持意义的标准：一致性、完全性
• 【五】递归现象
• 【六】意义的层级、可理解性
• 【七】命题演算
• 【八】某命题演算系统
• 【九】对命题演算系统编码
• 【十】层次现象
• 【十一】从不同层次理解大脑
• 【十二】思维是可理解的
• 【十三】递归集在程序领域中的意义
• 【十四】哥德尔不完备定理
• 【十五】思维现象：跳出系统
• 【十六】思维现象：自指、重复
• 【十七】是否存在“银弹”
• 【十八】AI目前的进展
• 【十九】AI可能的突破点
• 【二十】思维现象：怪圈

关于此书

• 本书是人工智能领域影响深远的一本奇书，书中大量的篇幅在解释哥德尔不完备性定理，并将其与其他领域的例子对照，包括艾舍尔的画以及巴赫的音乐。企图通过这种方式来对人类的认知进行深入的理解，为人工智能领域提供理论基础和探索的思路。

• 作者：Douglas R. Hofstadter（侯世达）
  • 侯世达是一位跨学科的通才，但是他将自己的研究领域定义为认知科学。他对计算机程序准确而创新的描述，以及对我们大脑中“秘密软件的结构”的描绘，开启了一代人对人工智能的探索。
• 简介：
  • 集异璧－GEB，是数学家哥德尔、版画家艾舍尔、音乐家巴赫三个名字的前缀。《哥德尔、艾舍尔、巴赫书：集异璧之大成》是在英语世界中有极高评价的科普著作，曾获得普利策文学奖。它通过对哥德尔的数理逻辑，艾舍尔的版画和巴赫的音乐三者的综合阐述，引人入胜地介绍了数理逻辑学、可计算理论、人工智能学、语言学、遗传学、音乐、绘画的理论等方面，构思精巧、含义深刻、视野广阔、富于哲学韵味。
  • 中译本前后费时十余年，译者都是数学和哲学的专家，还得到原作者的直接参与，译文严谨通达，特别是在原作者的帮助下，把西方的文化典故和说法，尽可能转换为中国文化的典故和说法，使这部译本甚至可看作是一部新的创作，也是中外翻译史上的一个创举。
• 评价：
  • "Every few decades an unknown author brings out a book of such depth, clarity, range, wit, beauty and originality that it is recognized at once as a major literary event. This is such a work" ——Martin Gardner, Scientific American
  • "In some ways, Godel, Escher, Bach is an entire humanistic education between the covers of a single book. So, for my next visit to a desert island, give me sun, sand, water and GEB, and I'll live happily ever after." ——John L. Casti, Nature
  • 被称为人工智能的《圣经》
  • 曾获得“普利策非小说奖”

形式系统

key point：

• 形式系统（Formal System）为包含字母、字的集合及由关系组成的有限集合。
• 公理：一个形式系统中所认可的真理。
• 定理：由形式系统中的公理以及该形式系统所定义的一系列规则所推出的一个陈述。
• 判定过程：一个能够在有限时间内检验一个定理是否成立的测试。
• 常用的形式系统有：语言、数理规则和逻辑。其中由于数学的研究对象是形式系统中唯一天生的逻辑自洽系统，因此数学也被一些人称为：形式科学。而语言大类中，部分为逻辑自洽的形式系统，如计算编程用的各类程序语言等。
• 用箭头以及偏序关系老描述的系统也属于一种形式系统。而所有的数据结构都可以用偏序集来表示，因此，我们可以认为这个世界本身就是由无数的形式系统所组成的，只是我们在日常生活中并没有察觉。

假如将现实世界视为一个形式系统，并假定物质的可分性是有尽头的。那么我们将组成物质的最小的粒子定义为“单子”，物理定律就是这个形式系统的规则，而这个系统唯一的公理就是这个系统初始状态下的所有粒子的分布状态。那么这个形式系统的定理就是某一时刻整个宇宙中的粒子分布状态。从广义的意义上来看，我们的世界都可以利用形式系统来表述，即用一组规则以及一套符号系统就能将整个世界都表述出来，并进行计算。数学是这类形式系统中最典型的例子。人们用一系列规则，用数字、英文字母还有一套符号来描述想要解决的问题。但形式系统与我们想要描述的问题应该如何对应？这就是“同构”的意义。

怪圈

• 当我们向上（或向下）穿过某一种层次系统中的一些层次时，会以外的发现我们回到了开始的地方。即一种“缠结的层次结构”。
• eg1：无穷升高的卡农——巴赫《音乐的奉献》
• eg2：视觉化的悖论——艾舍尔的画
• “怪圈”的圈
  • 圈可以是艾舍尔的画作中不符合现实逻辑的一个闭环，也可以是巴赫的无穷升高最后回到原来去掉的一个音阶。这些圈都有一个共同特点——运用了自指。
  • 递归就是一种自指的过程，在过程中不断地用同一套方式生成新的“东西”，这里的东西可以是画中的某个元素，也可以是形式系统中的一个定理。
  • 对于一个递归系统，首先要有一套递归的模式，这套模式能够利用系统中已有的公理来不断地生成新的定理。而如果一个系统所包含的定理是有限的，那么这个系统中递归处的定理越来越多，它的可预测性也就越来越小。
  • 对于复杂到一定程度的递归系统，就可能具有强有力的足够打破原本这个递归系统的规定的模式。那么这个递归系统就可以作用与自我本身，进行自我的扩展、改进、推广、加固。
  • “怪圈”的圈，其实就是一个“反馈环”

Error creating thumbnail: Unable to save thumbnail to destination

• “怪圈”的怪
  • 我们之所以会觉得“怪”，是因为我们是人。对于一台计算机而言，艾舍尔的画作对于它而言就是一个储存着每个像素点的颜色信息的矩阵，它并不能领悟到其中的含义。而如果让计算机跑一个存在怪圈的代码，在没有给它停止的指令之前它就不会停下。而如果让一个人来做同样的计算，过一段时间不管是谁都会发现这个怪圈的存在，并理解这个问题不能停下这一性质。所以，从某种意义上而言，怪圈的“怪”其实就是智能的本质。
  • 如右图，在这个递归规则中出现了一个怪圈，因此，我们可以利用这个规则生成无限数量的表达式。
  • 由于所有的数据结构都可以近似用偏序集来表示，并且包含怪圈的数据结构也能够用偏序集表示。因此，我们可以在计算机上实现这样的怪圈，而这样的怪圈也是创造出人工智能的必不可少的条件之一，是人工智能的基础。
• 哥德尔不完备性定理——“每个数学系统都存在永远无法被证明的语句”
  • 哥德尔对这个定理的证明思路正是想要构造一个“怪圈”，他的主要策略是把关于某个公理系统的语句映射到一个特定的系统内的语句，即映射到一个关于数字的语句。这个映射使公理系统能够有效地谈论自身。

层次

• 现实生活中我们一般用尺度来区分层级，例如从一个人到组成这个人的器官到组成这个器官的一个细胞，再到分子、原子等尺度。因此，我们可以用一个树状图的形式来表示这样的层级关系。如果用单一的一个点表示一个层级，有向箭头表示层级之间的包含关系，那么我们在现实生活中能够遇到的尺度上区分的层级都是一个树状图的形式，在这个图中不会出现回圈。也即是说，低层次的层级不能包含高层次的层级。
• 但是，如果我们利用其他的方式来划分层级，我们就能在层级的树状图中创造这样的回圈。例如，虚拟与现实也是一种划分层级的方式。许多电影中都利用了这样的技巧，将虚拟与现实的层级相混淆。《盗梦空间》就利用现实与梦境以及梦中之梦的层级划分，来构成了一个回圈。电影中的主角能够通过现实进入梦境以及梦境中的梦境，而主角对深层梦境产生的影响能够一层一层的向现实传递，最终改变现实。现实相对于梦境应该为高层次的层级，因为现实包含了梦境，而梦境无法影响到现实。但是电影中的设定让梦境也能够影响现实，因此就形成了“怪圈”，才有了精彩的电影剧情。其他的例子还有很多，例如现实中的小说家在小说中构思了一个漫画家，而小说中漫画家在漫画中构思了一个和现实生活相同的小说家。这些电影都巧妙的混淆了层级，让层级的树状图中形成“怪圈”。
• 艾舍尔就是一位非常擅长创造“怪圈”的画家，他的画中经常会出现这样的层次混淆。在下面这幅画中，一个男孩在看一幅画，画中的建筑也延伸出来，而男孩则被包含在了建筑之中。艾舍尔利用人们的视觉效果将画中的世界与画中的画的这两个层次混淆在了一起，构造出了一个“怪圈”。
• 而艾舍尔在画的中央并没有画出内容，在中央的这个位置会出现奇怪的扭曲。类似于数学中的“奇点”。几个层级在中心这个点的位置相交，如果画出中心点的内容则会将整幅画的不合理之处暴露出来。那么这样的点是否是“怪圈”中的一个普遍现象呢？至少在艾舍尔的画作中，总会出现那么几个不正常的点。也就是在利用人们视觉效果的时候，为了将几个层级混淆在一起时所改变的关键的那一部分。

完备性与一致性

• 对于一个形式系统而言，若果说它具有一致性，则由这个形式系统规定的公理所产生的任何陈述都属于这个形式系统的一个定理；如果说一个形式系统具有完备性，则所有的定理都可以由这个形式系统所规定的公理产生。此处的所有定理指的是在这个形式系统所处于的整个体系中的所有定理。
  • eg：例如在整个复数体系之中，如果一个形式系统只规定了实数域上的运算方式，那么这个形式系统就不能处理根号负一这样的情况。因此，这个系统不具有完备性，但它具有一致性。然而当我们将这个形式系统夸大到复数领域，他就具有了可以解释根号负一这样的“定理”。
• 类比唱片机（借用书中的例子）
  • 我们知道，对于任何一个物体，都存在一个共振频率。当这个物体以该频率震动时就会发生共振，从而损坏该物体。由这个性质，我们可以推出：没有一个唱片机能够完美的重现任何唱片上所刻画的声音频率。也就是说，如果一个唱片机能够重现所有声音频率；但是对于任何一个唱片机，都无法重现与他的共振频率相同的那一种声音。因此，这里就形成了一个“怪圈”。
  • 哥德尔不完备性定理说的就是这么一回事。通过这一例子可以对其有个初步理解。

哥德尔不完备性定理

定理内容

• 哥德尔不完备性定理包含两条定理：（1）任何自洽的形式系统，只要蕴涵皮亚诺算术公理，就可以在其中构造在体系中不能被证明的真命题，因此通过推理演绎不能得到所有真命题（即体系是不完备的）。（2）任何逻辑自洽的形式系统，只要蕴涵皮亚诺算术公理，它就不能用于证明其本身的自洽性。
  • 哥德尔不完备定理破坏了希尔伯特计划的哲学企图。大卫·希尔伯特提出，像实分析那样较为复杂的体系的兼容性，可以用较为简单的体系中的手段来证明。最终，全部数学的兼容性都可以归结为基本算术的兼容性。但哥德尔的第二条定理证明了基本算术的兼容性不能在自身内部证明，因此当然就不能用来证明比它更强的系统的兼容性了。
  • 哥德尔定理说明了一个形式系统中若满足定理中所提出的条件，则存在不可被证明的真命题。

定理证明

• 正如前文在怪圈一节中所指出的，哥德尔不完备性定理的证明的重要思想就是创造一个“怪圈”。而想要创造这样的怪圈就必须包含自指，但也正如前文所提到的，包含自指就很容易陷入无穷的递归当中，也就是“怪圈”。但哥德尔用一套巧妙的方法解决了这个问题。下面是一种不太严谨的简单的说明方式。
  • 每个公式或命题都可以被赋予一个哥德尔数。例如，将一个形式系统中的所有符号（包括数字符号）都用从1开始的自然数编码。那么一个形式系统就可以用一串数字进行表示。
  • 定义一个公式（*），其中的*为一个自由变量。我们将这个自由变量成为一个命题形式。当*被一个数代替时，（*）就是一个可以被证明或被证伪的一个特定命题。而对于（*）而言，其本身也是一个命题形式，也对应一个哥德尔数。
  • 我们定义：当且仅当把命题形式*的哥德尔数 (*)代入*中所得的命题 ( (*))是不可证明的，我们成（*）为不可自证的命题形式。
  • 构造一个命题形式 (*)，表示*是某个不可自证命题形式的哥德尔数。 对于（*）不可自证这一表述，我们用=（*）来代替。考虑=（（*））这一个命题，他相当于在问“这个不可自证的命题是否为不可自证的”。这样就成功的构造了一个怪圈。如果*是可证明的，于是 ( (*))为真，根据 的定义， = (*)就是某个不可自证命题形式的哥德尔数。于是*是不可自证的，根据不可自证的定义， ( (*))是不可证明的。这一矛盾说明*是不可证明的。如果*是可证伪的，则根据*的定义， = (*)就不是不可自证命题形式的哥德尔数。这意味着*不是不可自证的。根据不可自证的定义，我们断定 ( (*))是可以证明的，推出矛盾。这说明*的否定也是不可证明的。

再看哥德尔定理

哥德尔定理（它同样适用于其他理论），虽然是描述数学对象，但在根本上体现的是我们的思维的逻辑原则，即哥德尔定理最终是描述我们的思维逻辑的，即回到了我们的第五重境界上--------有这样的笑话：某个人轻轻咬一下身体的任何地方就会出现血迹，去医院检查而找不到原因，最后发现只是自己牙龈出血------或者类似于这样的例子：你发现你看任何物体都是模糊的，那么，你是应该怀疑这个世界正在消失呢，还是检查一下你的眼镜是不是脏了----我是说：当我们认为数学对象或物理系统具有哥德尔现象时，是否仅仅是意味着我们的思维逻辑存在着哥德尔逻辑。

回到哥德尔原理之所以可以用在我们所有的可设想的系统中，是因为，我们的思维产生这样的可设想系统和产生哥德尔定理的认识所依赖的逻辑是一样的：哥德尔定理的深刻性就在于我们通过形式系统的不完备性，对我们的思维的逻辑有了一个成像，尽管，我们出于谨慎和保守，认为哥德尔定理只适用于数学系统，但数学系统本身就是我们思维的创建，同时，在“万物皆像”的背景下，整个世界都是我们思维的创建。哥德尔定理在本质上描述的是我们的思维的内在逻辑结构。

哥德尔定理对形式系统有一个要求，那就是这个系统要足够强大。我们之所以要求形式系统必须足够强大，其本质原因就在于：形式系统展开后必须延伸到足够远，以至于可以产生差异非常大的结论--------而自我言说之所以容易产生矛盾，是因为，我们在形式系统中选择了一个特定的方向，即对自己进行谈论，那么，谈论的对象是一样的，但如果谈论的内容（结论）不同，我们就可以认为产生了矛盾，例如“这句话是错的”--------它可以沿着两个方向进行相似性的展开（推理），一个方向是，如果这句话是对的，那么，这意味着，这句话（自己）是错的；另一个方向是，如果这句话是错的，那么，这意味着，这句话（自己）是对的---------这就导致了矛盾----------这个矛盾你可以理解为：两个平等的方向上，得到了对自己不同的描述结果（一个是对的，一个是错的）--------即不可判定。

最广义的哥德尔原理：对于你设想或建构出来的任何一个足够强大的确定性系统，都必然存在要么不完备要么矛盾的问题。

人工智能与哥德尔不完备性定理

人工智能的提出

1956年，在美国青年学者约翰·麦卡锡的倡议下，一批数学家、信息学家、心理学家、神经生物学家和计算机科学家召开了人工智能历史上著名的“达特茅斯”会议，该会议上将这一新的学科正式命名为人工智能（Artificial Intelligence, AI），并将该学科的目标定位为设计具有真正智能的机器。在过去的几十年中，人工智能领域取得了一系列的成就，譬如：1956年，塞缪尔设计出一个跳棋程序，该程序能从棋谱中进行学习，也能从实践中总结经验，并于1962年打败了美国一个州的跳棋冠军；1959年，美籍华裔逻辑学家王浩设计的程序在IBM 704机器上仅用8.4分钟就证明了《数学原理》中的全部370条逻辑定理；上个世纪八十到九十年代，用于医疗诊断和其他各种用途的专家系统被大量商业化；1997年5月，IBM计算机“深蓝”成功地打败了国际象棋世界冠军卡斯帕罗夫；2005年，斯坦福大学设计的机器人车辆成功地在沙漠中完成自主导航驾驶131英里。

而人工智能的智能是否能称为真正意义上的“智能”？机器是否能够达到人类的智能水平？目前，许多人提出过对人工智能的无法成为真正的“智能”。甚至被称为“现代电子计算机之父”的约翰·冯·诺依曼就明确地表示“计算机决不会具有智能”。而他们反驳人工智能的理论基础之一就是哥德尔不完备性定理。

人的认知与机器的区别

人的认知过程其实可以视为我们人类不断接受外部信息，并对其进行计算的过程。而人工智能是一种基于计算机执行算法的过程。所谓的计算，实际上可以视为对信息的处理，即一种信息熵的流动。

结论

人的智能是一种高层次所具有的现象，意识和认知的核心是“怪圈”。我们对于认知还处于非常初步的阶段。

Curriculum Content

Week 3

Theme: 复杂系统: 从生物、数学、 物理、到社会

• 科学研究的三个焦点：
  • 第一：范式所揭示的事物之本质；
  • 第二：虽普遍但较少的事实判定（边界条件）；
  • 第三：与实证数据相匹配的范式
• 偏序集可用来趋近系统的各类结构，各类系统可以用偏序关系来表示，但是并不一定就是偏序集
• 通用算子的概念：
  • 所有命名空间都可以通过代数运算符生成
  • 所有命名空间应该共享一个通用的“时钟”
  • 命名空间应该是可扩展的
  • 名称空间身份验证应该是可扩展的和分布式的

Week 4

Theme: Story Telling

• 单子(Monad)：
  • 本周的课程中，老师从单子Monad的概念引入，通过单子的反差对应形成Composition。复合构图又分为水平复合构图(Horizontal Composition)以及垂直符合构图(Vertical Composition)。
• 几种箭头：
  • 1）比较两个对象的箭头——函数(Function)
  • 2）比较两个系统的箭头——函字(Functor)
  • 3）比较两个比较的方法——自然转换(Natural Transformation)
  • Summery：箭头也可以理解成函数间的映射，比较的层级越高，这个映射就越抽象，压缩性越高。
• 范畴论(Category Theory)
  • 可用来将我们已知的知识进行整理，简化。
  • Wikipedia可以作为这个过程的载体，作为一个词典。
  • 所有类型的事物都可以用箭头来表示，箭头提供了一个认知事物的统一的符号

Week 5

Theme: Historical Data, Writing, Accounting, and Causal Reasoning

• 文字的发明与记账的需求：
  • 卢卡·帕乔利Luca Pacioli在一本数学教科书（Accounting Balancing Equation）中发表：Asset = Liability + Equity
  • Assets = Liability + Equity and H = T + V：内在的统一性，金融与物理学之间的相通性。它们提供了一种分解保守资源总量的方法，因此允许迭代分支，从而实现连续复制。这种平衡和循环系统建立的思想是相同的，在生物或经济等复杂系统中同样适用。
• 记账方式的变革，给范式转移创造机会
• 最小的信息的单元：箭头
  • 1）基于箭头和标签可以实现逻辑推演，进行函数与多项式的运算
  • 2）利用箭头作为算元与算符可建立代数体系
• 解密：问题要可被描述，可建模，规则要有一致性，通用性。并且在一定的空间与时间的限制条件下，可以被解决。

Week 6

Theme：知识表达

• 所有的数据结构都是偏序集
• 函子是一种可以穿透多层次系统的数据映射机制，可表函子可将系统映射到一个集合范畴
• 两个问题之间同伦性
  • 可通过将系统拆分和整合，将两个看似不同的问题相互转换
  • 两个问题等价，可以与数学中最基础的“等于”类比，等价相当于更加抽象层次的等于。两个问题等价，就能使用同一套方法（系统）来解决。
• 系统工程
  • 系统工程中的难点在于跨领域的知识管理、模型复杂度高、定调过早导致机会被屏蔽。
  • 通过将系统的拆分和整合将一个复杂的系统的各个部分转化为已知的，已解决的一种方案，套用这种方案的格式来解决每一个小问题，再组装成一个复杂系统。
• 判断一个程序能否终止？
  • 将一个复杂的程序抽象成一个晶格化的点阵，将程序中复杂的对象都抽象成点。通过近似估计等方法计算点与点之间的距离，来判断程序需是否能够停止。

Week 7

（大作业报告）

Week 8

Theme：信息控制论(Cybernetics):控制与通信

Error creating thumbnail: Unable to save thumbnail to destination

• 利用如图所示的一组规则，递归的使用，可以获得无限数量的表达式
• Cybernetics：控制论与实际机器的关系是相似的，它的主题是“所有可能的机器”。控制论提供的是一个框架，并不是指单一的在机械系统不同部分之中进行控制的学科。在这个框架上，所有独立的机器都可以被订购、关联和理解，无论这个机器是人类创造的还是大自然中本身就有的。
• 所有的系统都可以被近似为偏序集
• 系统设计方法论的充分与必要条件
  • Soundness（可靠性）：所有可证明的真理都是真理，并且所有的真理都是可证明的
  • Precision（精确性）：命名空间的精确程度
  • Termination（可中止性）：该系统有一个判定过程，即可以在有限时间内得到一个系统的评估结果
• 控制类型：
  • 范畴理论的一个独特之处在于，它提供了一个元数学框架来反思自身。这可以在lambda演算和三种类型的函数中找到，即函子(表示其尾部或内容的头标签)、函数(允许某些中间替换操作的间接方法)、自然转换(一种指向自身的函数)被定义。
  • 这个数学框架只使用这三种类型的函数(函数是根类型)来表示一切。
  • 这种类型检查机制为检查和验证结构的所有变体以及任何名称空间中的值的完整性和完整性注入了一种通用的原则，因此它提供了最简洁但又最全面的抽象。
  • 这种通用机制已经被计算机器操作，提供了自动化和可扩展的类型推理，因此，它正在成为我们现代文明的基础层。
  • 我们社会不平等的根源就来源于这种机制的不正确或有偏见的执行。
    
• 系统的控制和通信；必须重新发现范畴理论和自然界其他拓扑结构中已经存在的规则和属性。
  • 系统的控制和通信不仅需要原始的内容，还需要一种结构来管理系统中实体之间隐式关系的解释。
  • 这一直是最大障碍，在大多数其他类型的数学框架中都没有解决，直到范畴理论的出现。
  • 目前，基于类型的解释框架可以在数学的许多领域找到，部分由于逻辑学、Lambda微积分和范畴理论的启示。
  • 所有这些隐式结构都是同构映射，也被称为“Curry-Howard-Lambeck对应”。
  • 正是由于这种一致性，以及这种一致性的普遍性，人们开始认为，所有的科学和数学原理只能被发现，而不能被发明，因为它们在人们发明之前就已经存在了。
  • 这与控制论有关，因为在控制和通信领域，许多思想和技术必须已经在数学和计算科学中发现和发展，因此控制论的技术和知识，

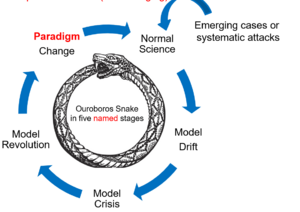
• 库恩理论的本质：（递归和对称性破缺recursion and symmetry-breaking）

Week 10

Theme：Artificial Intelligence and its Social Impacts

• 同学们讨论分享
• 现代技术与科技的发展以及知识体系的迅速扩大，不断地挑战着人类和人类社会的认知能力。我们需要一套有效的认知方式，来利用当代技术以及认知科学内容。而以维基等工具以及hyperlink、偏序集等理论知识为基础，我们可以建立起一套让一个团体（科学团体、大学生甚至是所有科研工作者）快速的对当下我们拥有的知识进行认知。
• 人工智能正在塑造集体意识的基础
  • 人工智能规定了一种用于计算操作和验证抽象规范的算法，将所有的数据类型转换为偏序集来进行枚举和求值。其中，对于不是偏序集的系统仍然能够用偏序集的方式来进行表示。
  • 控制论这个学科的完善以及通信技术的发展提高了治理的密度和准确性
  • 因此，可以利用这些工具可以创造一种通用的跨学科的认知方式

Book Report

关于实践

• 范式作为包含符号概括、模型、价值、方法的学术共同体的团体承诺的集合，同时表现为科学共同体共同仿效的研究实例（范例）。“范式作为共有的范例”这一洞见，反映了实践领域的重要问题。
• 《科学革命的结构》一书第五章详细探讨了规则与范式的关系，概括如下：范式作为规则系统，同时表现为共有的范例。科研工作者往往是从具体的范例中把握范式并指导常规科研实践，而非抽象地学习和服从规则，这是因为：首先，从范式中充分地总结出全部规则并得到科学共同体的普遍认可是难以实现的，因为范式的内涵十分丰富而难以抽象概括；其次，以人的有限性，即使能全部认识这些规则，也难以全面地遵从。常规科学工作者往往是在对范式的模拟中展开研究的，即面对新的问题时寻找其与熟悉的范例的相似之处，“照葫芦画瓢”，就像学生学习教材上例题后利用相似性去解答其他问题，这是不难实现的。
• 中国古代学问以实践为根本指向，以“即器存道”为基本方式，对其合理性和必要性深有醒觉。之所以要在具体的实践案例中学习如何实践，一方面因为实践原则十分丰富而难以抽象把握，另一方面因为只有具体实例才能感化内心，引发心灵深处的共鸣，实现知行合一。
• 无论是常规科学实践，还是人伦日用实践，都依靠即器存道。库恩在指明范式作为范例指导实践地同时，也强调当范式尚未确立或受到挑战时，其中规则的抽象概括和争论是必要的。同样地，在一般实践问题出现争执时，实践原则的抽象讨论也是必要的。因此，强调“即器存道”并非彻底否定“离器言道”。

不可通约性

• “不可通约性”无疑是本书的一个重要洞见。世界存在很多不可通约的不同体系，不仅具体观点不同，而且检验和比较不同观点的价值标准也不同，甚至就连一些最基本的认识（如概念的定义、对世界的观察）也大相径庭。
• 无论是认知世界的方式还是实践的取向都不只有一种模式，不同模式各有其合理性。站在一定的立场中去看待异己可能觉得其完全不可理喻，但在是非和善恶的判断中仍应当持谨慎态度。
• 其次是相对主义的问题。多元性是否一定导致相对主义，即认为不同取向（认知模式或行为方式）之间一律平等，不存在绝对的真理或普遍性的善——库恩对这一问题处理得很好。简而言之，没有绝对的体系，但有在体系之外的绝对的检验标准，例如科学范式的解题能力，或实践取向是否肯定生命。因此，多元性并不一定导致相对主义，多元性和普遍性可以也应当实现平衡。