Difference between revisions of "对科学革命、范式、科学共同体的再思考:以固体力学为例"
| (249 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
[[File:固体力学发展史.png|thumb|900px|right|发展史思维导图]] | |||
== | =对科学革命、范式、科学共同体的再思考= | ||
[[File:The Structure of Scientific Revolutions.pdf|400px|thumb|right|The Structure of Scientific Revolutions]] | |||
《科学革命的结构》([[wikipedia:The Structure of Scientific Revolutions|The Structure of Scientific Revolutions]]),1962年出版;于1970年再版;英文简写为SSR),是美国科学史家与科学哲学家托马斯·库恩([[wikipedia:Thomas Samuel Kuhn|Thomas Samuel Kuhn]])的著作。这本书的出版是历史,哲学和科学知识社会学的一个里程碑事件;在学术界内外,引发了连续广泛的评估和反响。库恩挑战当时对“常态科学”历程的主流观点。常态科学的历程被认为是由公认事实和理论“累积而发展”,而他认为:相对于常态科学这样累积连续概念的期间中,另外有一段被革新科学所中断的模式。在科学革新历程中发现的“异常现象”导出了新的范式,然后以此范例质疑旧数据的新问题,超过之前范式单纯的“解谜”,改变研究规则并指导新研究的“地图”。 | |||
托马斯·库恩在其著作《科学革命的结构》(以下简称《结构》)中系统地、独创性地对科学演进的过程进行了总结,并提出了影响深远的“范式”概念。《结构》将“范式”定义为:“某些实际科学实践的公认范例——包括定律、理论、应用和仪器”<ref name="Kuhn">{{:Book/科学革命的结构}}</ref>,而这种“公认范例”可以为特定的连贯的科学研究的传统提供模型。于是,科学演进的过程可以概括为:由建立在特定范式之上的“解谜”的常规科学,到出现既有范式无法解释或应对的反常,再到随反常现象而来的“显著的专业不安全感”从而引发危机,最终通过范式转换的方式完成科学革命,旧范式全部或部分地被一个与其完全不能并立的崭新范式所取代。这一概括以及背后的细节对科学工作者更好地认识科学发展以及在科学中自我定位起到了重要的参考和指导作用。 | |||
本文将结合'''《超越学科的认知基础》'''的课程,探讨以下三方面的内容:科学革命的过程与前后的科学知觉转变、新时期学科交叉环境下的科学范式、人在科学中扮演的角色以及行为准则。以上三条内容是基于《结构》中重要的概念:科学革命、范式、科学共同体的再思考。前两者聚焦于科学发展的历程,而后者聚焦于科学工作者在科学发展中的作用以及受到的影响。本文旨在从科学自身的发展和科学的参与者这两方面提出新的思考。 | |||
{{#ev:youtube|https://www.youtube.com/watch?v=L70T4pQv7P8|500px}} | |||
该视频简介了《科学革命的结构》与作者托马斯·库恩。 | |||
==科学革命与科学知觉的转换 & 态射([[wikipedia:Morphism | Morphism]])== | |||
科学演进的过程中伴随着'''科学知觉的转换''' <ref extends="Kuhn">p.94-113</ref>,尤其体现为科学共同体集体或其中有卓越贡献的个人的思维方式的变化,并且常规科学与渐进式的思维演变、'''科学革命'''与思维的跳跃往往有着良好的对应关系,如:《结构》中提到的天文学范式转变、王训教授讲座中提到的赵忠贤院士将铁基超导体的临界温度提升至超过麦克米兰极限,都是思维跳跃带来科学突破的范例。而另一方面,科学的演进,尤其是范式转换,也可以带来包括思维方式在内的科学知觉的转变,并且这种转变几乎内化为新范式的一部分。库恩强调:“科学接受一个新范式之后,将产生视觉的、知觉的及其他心理的转变,已至会以与以前不一样的方式来看这个世界,也可以说,生活于或工作于一个新的世界中<ref extends="Kuhn">p.94-113</ref>。例如《结构》中提到的:化学范式转变后,新范式下的化学家“在一个不同的世界里工作” <ref extends="Kuhn"> p.94-113</ref>,足以体现科学知觉发生的颠覆性变化。 | |||
对于今天的人类是否面对着新一轮的颠覆性科学革命,学界普遍的观点是:目前人类正处于第二次工业革命和石油世纪的最后阶段<ref>黄欣荣.大数据时代的思维变革[J].重庆理工大学学报(社会科学),2014,28(05):13-18.</ref>。而这是一个令人难以接受的严峻事实,因为这一现实将迫使人类迅速过渡到一个全新的能源体制和工业模式,而新的工业革命和经济革命必然以科学革命作为先导。而纵观当下世界,信息时代的全球信息的联通与共享、以及可再生能源发展初见成效,不难预见新的通讯技术与能源系统结合之际,即将来临的科学革命的基本样貌。 | |||
回顾自然科学发展的历史,其科学方法论从宏观来说主要由'''整体论'''和'''还原论'''这两种方法论体系构成,而整体论又随着西方科学的进步,特别是分析、还原科学的兴起而走向衰落<ref>钱学森,于景元,戴汝为.一个科学新领域——开放的复杂巨系统及其方法论[J].自然杂志,1990(01):3-10+64.</ref>。随着牛顿力学的巨大成功,还原论被近代科学视为一种万能的科学方法论用于刻画世界,并且取得了辉煌的成就。直到二十世纪90年代,基于超越还原论的'''复杂性科学'''逐渐兴起,沉寂千年的整体论也随着复杂性科学而逐渐复兴。在这场变革中,大数据技术和互联网技术以及背后蕴含的全新思维方式,发挥着相当重要的作用。《大数据时代》的作者舍恩伯格认为:“大数据开启了一次重大的时代转型,而大数据时代的变革首先是思维变革,继而影响商业变革和管理变革”<ref>《大数据时代:生活、工作与思维的大变革》舍恩伯格著,周涛译,浙江:浙江人民出版社,2012,第5页</ref>。同时他也指出了这种思维转变的核心特点:放弃对因果关系的渴求,而取而代之关注相关关系,即只需知道“是什么”而不去关注“为什么”。这恰恰颠覆了千百年来人类的思维惯性,具体还体现在:不关注随机样本,而是关注全体数据;不要求精确性,而是追求混杂性等等。由于大数据技术处理了所涉及问题的全部数据,这就使得整体论中全面、完整把握对象的思想有了完整的体现和科学的表述,而另一方面,对一个个具体数据的处理也部分应用了还原论中的方法。这也与过去科学中追求统一化、标准化的科学逻辑不同,人们无需再将问题在理论层面进行简化,把复杂、多样的东西首先通过还原论还原到一个基点,从而更加有助于科学工作者接近事实的真相。从科学方法论以及科学知觉转变的角度来说,即将到来的科学革命甚至要比以往任何科学革命来得更加彻底、有更深远的影响。 | |||
[[File:F.png|thumb|right|Function visualization]] | |||
[[File:Functor.png|thumb|right|Functor visualization]] | |||
[[File:Natural transformation.png|thumb|right|Natural transformation visualization]] | |||
[[wikipedia:en:Category theory|范畴论]]: 范畴代表着其他数学概念的抽象表示。 许多数学领域都可以被归化为范畴论中的范畴。因此,范畴论使用抽象来使陈述和证明复杂而微妙的数学结果以更简单的方式呈现。 | |||
[[wikipedia:Morphism | 态射]]:在数学尤其是范畴论中,态射是一种保持结构的映射,它从一个数学结构到另一个相同类型的数学结构。态射的概念在当代数学中多次出现。在集合论中,态射是函数;在线性代数中,线性变换;在群论中,群同态;在拓扑学中,连续函数等等。 | |||
该视频简介了抽象代数与范畴论中的基本概念,对于理解下文具有直接帮助。 | |||
{{#ev:youtube|https://www.youtube.com/watch?v=XPF5fe1WdKY|500px}} | |||
'''函数([[wikipedia:function|function]])定义:''' | |||
In [[wikipedia:mathematics|数学]]中,从 ''X''集合到 ''Y''集合的函数是''Y ''集合中的元素与''X''集合中的任一元素的对应关系。集合''X''称为 函数的[[wikipedia:domain of a function|定义域]] ,集合 ''Y'' 称为函数的[[wikipedia:codomain|值域]]。 | |||
'''函子([[wikipedia:functor|functor]])定义:''' | |||
Let ''C'' and ''D'' be [[wikipedia:category (mathematics)|categories]]. A '''functor''' ''F'' from ''C'' to ''D'' is a mapping that: | |||
* associates each object <math>X</math> in ''C'' to an object <math>F(X)</math> in ''D'', | |||
* associates each morphism <math>f \colon X \to Y</math> in ''C'' to a morphism <math>F(f) \colon F(X) \to F(Y)</math> in ''D'' such that the following two conditions hold: | |||
** <math>F(\mathrm{id}_{X}) = \mathrm{id}_{F(X)}\,\!</math> for every object <math>X</math> in ''C'', | |||
** <math>F(g \circ f) = F(g) \circ F(f)</math> for all morphisms <math>f \colon X \to Y\,\!</math> and <math>g \colon Y\to Z</math> in ''C''. | |||
'''自然转换([[wikipedia:natural transformation|natural transformation]])定义:''' | |||
If <math> F</math> and <math> G</math> are [[wikipedia:functor|functor]]s between the categories <math> C</math> and <math> D </math>, then a '''natural transformation''' <math> \eta</math> from | |||
<math> F</math> to <math> G</math> is a family of morphisms that satisfies two requirements. | |||
# The natural transformation must associate, to every object <math> X</math> in <math> C</math>, a [[morphism]] <math>\eta_X : F(X) \to G(X)</math> between objects of <math> D </math>. The morphism <math> \eta_X</math> is called the '''component''' of <math> \eta</math> at <math> X </math>. | |||
# Components must be such that for every morphism <math> f :X \to Y</math> in <math> C</math> we have: | |||
:::<math>\eta_Y \circ F(f) = G(f) \circ \eta_X</math> | |||
If both <math> F</math> and <math> G</math> are [[wikipedia:contravariant functor|contravariant]], the vertical arrows in this diagram are reversed. If <math> \eta</math> is a natural transformation from <math> F</math> to <math> G </math>, we also write <math> \eta : F \to G</math> or <math> \eta : F \implies G </math>. This is also expressed by saying the family of morphisms <math> \eta_X: F(X) \to G(X)</math> is '''natural''' in <math> X </math>. | |||
If, for every object <math> X</math> in <math> C </math>, the morphism <math> \eta_X</math> is an [[wikipedia:isomorphism|isomorphism]] in <math> D </math>, then <math> \eta</math> is said to be a '''natural isomorphism''' (or sometimes '''natural equivalence''' or '''isomorphism of functors'''). Two functors <math> F </math> and <math> G</math> are called ''naturally isomorphic'' or simply ''isomorphic'' if there exists a natural isomorphism from <math> F</math> to <math> G</math>. | |||
An '''infranatural transformation''' <math> \eta</math> from <math> F</math> to <math> G</math> is simply a family of morphisms <math>\eta_X : F(X) \to G(X) </math>, for all <math> X</math> in <math> C</math>. Thus a natural transformation is an infranatural transformation for which <math> \eta_Y \circ F(f) = G(f) \circ \eta_X</math> for every morphism <math> f : X \to Y </math>. The '''naturalizer''' of <math> \eta </math>, nat<math> (\eta) </math>, is the largest [[subcategory]] of <math> C</math> containing all the objects of <math> C</math> on which <math> \eta</math> restricts to a natural transformation. | |||
==学科交叉与范式 & 超链接 == | |||
[[File:2013-11-26-11 01 24-RosvallBergstromPNAS2008Full.pdf-Adobe-Reader.png|thumb|left|学科交叉网络-1]] | |||
[[File:2013-11-26-11 01 05-RosvallBergstromPNAS2008Full.pdf-Adobe-Reader.png|thumb|right|学科交叉网络-2]] | |||
上世纪后半叶起,新兴科学越发呈现出'''多学科交叉、综合'''的特点,这一定程度上也源于常规科学遇到的瓶颈。进入21世纪,交叉学科的迅猛发展正在为科学创新注入新的活力,也体现出科学向综合性发展的趋势。上至生物信息学、计算化学等已经初具规模的新型学科,下至迅速转化交叉学科科研成果的工程应用,如智能硬件、纳米材料等等,学科交叉带来的创造力可见一斑。在2020年听过的[[wikipedia: Andrew Yao|姚期智]]教授的一次讲座中,他由自己从物理学研究转向当时新兴的计算机科学研究的个人经历,说明了多学科知识储备对于学术研究的重要作用。物理方面深厚的专业基础,使他在进入量子计算的全新领域时可以游刃有余,不会过多地理论学习所困扰。而其引领的量子计算领域,相比传统计算在效率方面有巨大的飞跃,充分体现出学科交叉的强大能量。姚先生的经历也启示着未来从事科研的科学工作者,广泛涉猎各学科的知识,从而在学科交叉点发现更多创新的基点。而[[wikipedia:Andrew Yao|姚期智]]院士的讲座中曾介绍一代大师[[wikipedia:Alan Turing|阿兰·图灵]]的介绍,亦体现出学科交叉与多学科知识储备的重要性。图灵先生青年时期接受的宽口径自然科学教育使得他可以在人工智能和数理生物学等多学科领域取得颠覆性的成就。 | |||
交叉学科的'''范式''',相较于传统学科的范式,或许具有更多的进步性特征。由于它承载于众多学科的底层逻辑之上,而每个学科发生的反常,都会对交叉学科产生直接影响。因此,交叉学科更容易通过各种反常情形发现完善范式的方向。而另一方面,由于各学科的相互牵制,在一定程度上,交叉学科的范式转换更难完成。如果仅有底层学科其中之一的理论飞跃,则难以使交叉学科的范式产生革命性的发展。交叉学科范式转换应该是底层学科范式联动转换,全面进步的结果。 | |||
库恩的理论在学科交叉的情景下有很大的不适用性,[[于舒昂]]同学在[[于舒昂 感悟]]一节中指出了库恩理论的一些时代局限性。库恩的理论阐述了:“一个科学工作者只能属于一个特定的科学共同体”,但这在如今学科交叉广泛存在的科学界是不切实际的。 | |||
[[wikipedia: paradigm|Paradigm]]: 在科学和哲学中, 范式 (Paradigm,/ˈpærədaɪm/) 是一组不同的概念或思维模式,包括理论、研究方法、假设和标准,这些标准构成了一个领域的贡献。 | |||
==“人”的科学与科学共同体 & 命名空间([[wikipedia:namespace|Namespace]])== | |||
[[File:Opensource.jpg|thumb|left|开源-词云]] | |||
[[File:OpensourceTree.png|thumb|right|开源-软件树]] | |||
科学归根结底是'''“人”的科学''',它是人类文明的产物。库恩在《结构》中也提及了很多关于人与科学关系的内容:“在范式确立前的科学模式中,科学团体缺乏共同的研究信念,不同研究者的工作要从奠基做起,选取的方法与支撑理论个人色彩强烈,科学工作者的著作多与其他学派的成员进行对话”<ref extends="Kuhn">第9-22页</ref>;又如:“科学的改宗往往会受到很多非科学因素的影响,而其本质是社会中的人的影响”。《结构》中还界定了“'''科学共同体'''”的概念:“一个科学共同体由同一个科学专业领域的工作者组成,他们受到近似的教育和专业训练,研究过相似的界定该科学学科界限的文献”<ref extends="Kuhn">第9-22页</ref>。从而,常规科学和科学革命都在科学共同体的活动的基础上展开,范式的概念也紧紧依附于科学共同体,库恩称其为:科学共同体“团体承诺的集合”、“共有的范例”。 | |||
朱邦芬教授的讲座中提到了一些学术共同体对其成员科学研究产生影响的例子,如:黄昆先生从黄方程的建立,极化激元概念的提出,到多声子跃迁理论的开创,其中反映出一个好的研究群体对其中个体成员发现和提出好的研究问题的启示作用;以及学术共同体的传承中,导师或前辈对后来者的影响集中体现在思维风格,而非简单的知识传授。又以居里夫人为例,说明了个人的品格对其学术成就的影响。同时指出:“创造知识方面的缺陷往往源自学习知识时的一些问题,也受限于人格的养成。”由此,可以更加深刻地认识通识教育的意义,通识教育所培养的独立思考和判断的能力,对于未来的科学研究具有重要的影响。如爱因斯坦所说:“青年人在离开学校时,是作为一个和谐的人,而不是作为一个专家。” | 朱邦芬教授的讲座中提到了一些学术共同体对其成员科学研究产生影响的例子,如:黄昆先生从黄方程的建立,极化激元概念的提出,到多声子跃迁理论的开创,其中反映出一个好的研究群体对其中个体成员发现和提出好的研究问题的启示作用;以及学术共同体的传承中,导师或前辈对后来者的影响集中体现在思维风格,而非简单的知识传授。又以居里夫人为例,说明了个人的品格对其学术成就的影响。同时指出:“创造知识方面的缺陷往往源自学习知识时的一些问题,也受限于人格的养成。”由此,可以更加深刻地认识通识教育的意义,通识教育所培养的独立思考和判断的能力,对于未来的科学研究具有重要的影响。如爱因斯坦所说:“青年人在离开学校时,是作为一个和谐的人,而不是作为一个专家。” | ||
现代科学的两大基石:形式逻辑推理和实验检验均基于求真的要求并保证结论趋近于真实,因此,人作为科学的主体,必须有可以凭借的事物以限制所从事的科学的严谨与规范,于是,在不同的科学共同体中形成了相应的学术规范与判断准则。在严格的规范框架下,对自然运行的个体观察才可以呈现给他人,并被他人独立判断其有效性之后转换为科学共同体的学术共识。因此,良好的学术环境应该具有这一特点:驱使科学工作者维护科研诚信并重视自己及团队的学术声誉。 | 现代科学的两大基石:形式逻辑推理和实验检验均基于求真的要求并保证结论趋近于真实,因此,人作为科学的主体,必须有可以凭借的事物以限制所从事的科学的严谨与规范,于是,在不同的科学共同体中形成了相应的学术规范与判断准则。在严格的规范框架下,对自然运行的个体观察才可以呈现给他人,并被他人独立判断其有效性之后转换为科学共同体的学术共识。因此,良好的学术环境应该具有这一特点:驱使科学工作者维护科研诚信并重视自己及团队的学术声誉。 | ||
[[wikipedia: namespace| 命名空间]]: 在计算中,命名空间(namespace)是一组符号(名称),用于识别和引用各种类型的对象。命名空间确保给定的所有对象都有唯一的名称,以便容易识别它们。 | |||
命名空间的结构通常为层次结构,以允许在不同上下文中重用名称。作为一个类比,考虑一个命名系统,其中每个人都有一个名字,以及与他们的亲戚共享的姓氏。如果家庭成员的名字只在每个家庭中是唯一的,那么每个人都可以通过名字和姓氏的组合来唯一地识别;只有一个无名氏,虽然可能有很多叫Jane的人。在Doe家族的名称空间中,仅仅“Jane”就足以明确地指定这个人,而在“全局”的命名空间中,必须使用全名才有可能确认到个体。 | |||
== | =学科演进的例子:固体力学= | ||
===“胡克定律”=== | 该视频简介了固体力学的发展史、基本假设及基本概念。 | ||
{{#ev:youtube|https:/https://www.youtube.com/watch?v=d9AbPLAwKaI|1200px|center}} | |||
==弹性力学([[wikipedia:Elasticity (physics)|Elastic mechanics/Elasticity]])== | |||
===[[wikipedia:Hooke's law|“胡克定律”]]=== | |||
[[File:Hook Law.png|thumb|left|应力应变关系]] | |||
弹性理论范式形成初期的工作是通过实践、探索弹性力学的基本规律。1678年,英国科学家胡克([[wikipedia:en:Robert Hooke|Robert Hooke]])在他的著名论文《恢复原形的或弹簧的势能》中用拉丁文“Ut tension sic vis” 首次阐述了“任何弹簧的力与它的伸长按同一比例增加,即力与变形成正比关系”的规律。 胡克提出该定律的过程颇有趣味,他于1676年发表了一句拉丁字谜,谜面是:ceiiinosssttuv。两年后他公布了谜底是:ut tensio sic vis,意思是“力如伸长那样变化”紧接着,1680年,法国科学家马略特([[wikipedia:en:Edme Mariotte|Edme Mariotte]])又独立地发现了这一定律,二人分别对自己的发现进行了大量的实验验证。在随后的三百多年中,弹性力学的几乎一切工作都在胡克定律的基础上展开: | |||
:<math>F_s = kx</math> | |||
值得一提的是,早在胡克之前,我国东汉时期的学者郑玄既提出过类似的规律。他在注释《考工记·弓人》中“量其力,有三均”这句话时,记录了以下文字:“假令弓力胜三石,引之中三尺,驰其弦,以绳缓擐之,一石,则张一尺”。这里的文字展示了古代中国人测量弓弩的刚度时所发现的“力与伸长成正比”的定律。然而,长久以来,这一规律仅仅作为生产生活中检验、制造的经验规则,并没有被人们深入地探究及验证,没有成为真正意义上的科学。 | 值得一提的是,早在胡克之前,我国东汉时期的学者郑玄既提出过类似的规律。他在注释《考工记·弓人》中“量其力,有三均”这句话时,记录了以下文字:“假令弓力胜三石,引之中三尺,驰其弦,以绳缓擐之,一石,则张一尺”。这里的文字展示了古代中国人测量弓弩的刚度时所发现的“力与伸长成正比”的定律。然而,长久以来,这一规律仅仅作为生产生活中检验、制造的经验规则,并没有被人们深入地探究及验证,没有成为真正意义上的科学。 | ||
即使十七世纪的胡克定律,也存在着一定的瑕疵。例如:1691年,在莱布尼兹([[wikipedia:en:Gottfried Wilhelm Leibniz|Gottfried Wilhelm Leibniz]])和惠根斯([[wikipedia:en:Christiaan Huyghens|Christiaan Huyghens]])的通信中,惠根斯透露其在重复胡克的实验时,仅当弹簧轻微伸长时,实验结果才与理论一致。事实上,最初的胡克定律未能注意到这种简单线性关系的适用范围问题,对于大变形或者塑性变形等各种几何非线性和材料非线性情况,力与变形便不再是正比关系。反常的出现,使得弹性理论范式不断被完善、发展。 | |||
===柯西和纳维的奠基性工作=== | ===柯西和纳维的奠基性工作=== | ||
自胡克之后,越来越多的科学家开始尝试建立研究弹性体问题的通用理论架构。这一阶段,人们还是主要使用粗糙的、不完备的理论来处理简单构建的力学问题,其中欧拉([[wikipedia:Leonhard Euler|Leonhard Euler]])、伯努利([[wikipedia:Daniel Bernoulli|Daniel Bernoulli]])等人的工作取得了一定的突破,尤其在关于梁、板的理论方面。同时,数学工具的发展,使得建立弹性力学数学理论的条件已大体具备。十九世纪20年代,纳维([[wikipedia:Navier|Navier]])和柯西([[wikipedia:Cauchy|Cauchy]])的工作,完整地建立了弹性力学范式的数学理论大厦。 | |||
柯西在1822~ | 1821年,纳维向法国科学院提交了他的论文《弹性固体的平衡定理与运动的研究报告》,在弹性体的分子理论上有了更进一步的成就,在纳维推导出的各向同性弹性体的平衡微分方程中,利用他提出的假设来求物体的弹性仅需一个常数即可。随后,柯西综合了纳维的推导并研究了各项异性的弹性体,并指出:在最普遍的情况下,要决定物体的弹性需要15个常数。柯西更大的贡献在于他借鉴水力学中平面上压力的概念,引入了应变和应力,以代替个别质点间分子力的研讨。柯西本人利用这套理论研究过矩形杆件的变形,也为后来圣维南([[wikipedia:Adhémar Jean Claude Barré de Saint-Venant|Adhémar Jean Claude Barré de Saint-Venant]])推导出完整的棱柱杆扭转理论建立了基础。 | ||
柯西在1822~1828年发表的几篇论文中,明确了如应力([[wikipedia:Stress (mechanics)|Stress]]),应变([[wikipedia:Strain (mechanics)|Strain]]),应力分量,应变分量等一系列概念,建立了弹性力学的几何方程、平衡方程、各向同性以及各向异性材料的广义胡克定律,从而打开了弹性力学向纵深发展的突破口。 | |||
=== 线性各向同性弹性力学大发展 === | === 线性各向同性弹性力学大发展 === | ||
19世纪中叶,圣维南运用弹性力学的基本方程和他自创的半逆解法([[https://www.researchgate.net/publication/259458856_The_Semi-Inverse_Method_in_solid_mechanics_Theoretical_underpinnings_and_novel_applications| semi-inverse method]]),奠定了柱体扭转理论研究的基础,也标志着线性各向同性弹性理论大发展时期的到来。利用半逆解法,只需假定位移和力的一些特征,就可以推断出这些量的其余特征使其能满足所有的弹性方程,并且运用该方法得到的理论结果与实验结果密切吻合,因此他本人断言:“凡是学过基本材料力学近似解的工程师都能用这个方法得出有实用价值的精确解来”。圣维南为弹性理论范式的完善做出了卓越的贡献,以至于在托德亨特([[wikipedia:Issac Todhunter|Todhunter]])与皮尔逊([[wikipedia:Karl Pearson|Karl Pearson]])合著的《弹性力学史》的扉页上,都写有“为了纪念近代最先进的弹性学家圣维南,编者谨以编著此书的劳力奉献给他”的献词。 | |||
这一时期的标志性特征还有:发展了许多有效的近似计算、数值计算方法,例如著名的“瑞利- | 在随后的几十年中,1881年,德国科学家赫兹([[wikipedia:Heinrich Rudolf Hertz|Heinrich Rudolf Hertz]])解决了两弹性体局部接触时弹性体内的应力分布问题,1898年,基尔施([[wikipedia:Ernst Gustav Kirsch|Kirsch]])发现了应力集中现象……诸多理论突破解释了过去一些反常的实验现象,同时,新的理论也广泛地运用于解决工程问题,弹性力学得到了工程界的重视,在提高机械、结构等零件设计水平方面起了重要作用。 | ||
这一时期的标志性特征还有:发展了许多有效的近似计算、数值计算方法,例如著名的“瑞利-里兹法”。这一方法于1877年,由英国科学家瑞利([[wikipedia:John William Strutt|John William Strutt]])在《声学理论》中首先使用,随后又被瑞士科学家里兹([[wikipedia:Walther Ritz|Ritz]])于1908年作为一种有效方法提出,它不光大大提高了弹性理论解决实际工程问题的能力,同时也推动了物理等其他相关学科中近似计算的蓬勃发展。 | |||
===弹性理论的全新机遇=== | ===弹性理论的全新机遇=== | ||
20世纪后,弹性力学的经典理论仍在不断完善,同时也被科学家作为探讨许多复杂问题的有效工具,出现了相关联的边缘范式和交叉范式。例如:考虑温度影响的热弹性力学,研究固体同气体、液体相互作用的气动弹性力学、水弹性力学,以及适用范围更广的各向异性和非均匀体的理论,非线性弹性力学等等。不同学科的紧密配合与联系正在为弹性力学的发展注入新的活力,这些新领域的发展,亦将直接促进相关工程技术的进步。 | 20世纪后,弹性力学的经典理论仍在不断完善,同时也被科学家作为探讨许多复杂问题的有效工具,出现了相关联的边缘范式和交叉范式。例如:考虑温度影响的热弹性力学,研究固体同气体、液体相互作用的气动弹性力学、水弹性力学,以及适用范围更广的各向异性和非均匀体的理论,非线性弹性力学等等。不同学科的紧密配合与联系正在为弹性力学的发展注入新的活力,这些新领域的发展,亦将直接促进相关工程技术的进步。 | ||
==塑性力学([[wikipedia:Plasticity (physics)|Plastic mechanics/Plasticity]])== | |||
[[File:Deformation.png|thumb|Deformation theory]] | |||
塑性力学的本质是一种用来描述材料的塑性行为的理论。一旦材料发生塑性行为,材料的应力应变关系不再是线弹性的,这个时候就需要新的数学描述,这套基于材料塑性行为发展而来的理论就是塑性力学,其与弹性最大的区别就是存在不可恢复的塑性变形。 | |||
:<math>\sigma = C:\epsilon-\epsilon_p</math> | |||
上式表明,如果我们知道了应变和塑性应变,我们就可以知道这一点的应力,而在弹性力学中我们仅仅需要知道应变就可以知道一点的应力。于是乎,一种标准的用来描述这种情形的框架被提了出来,这套框架明确回答了:塑性会在何时发生的问题('''屈服函数'''),塑性发生时塑性应变的变化('''流动法则'''),塑性变形时材料强化的问题('''强化法则''')以及其他补充的条件。 | |||
===数学描述=== | |||
====变形理论==== | |||
塑性力学有若干种数学描述,其中一种是变形理论(如胡克定律):柯西应力张量(d-1阶)是应变张量的函数。虽然当一小部分物质受到不断增加的载荷(如应变载荷)时,这种描述是准确的,但这一理论不能解释不可逆性。韧性材料可以承受较大的塑性变形而不断裂。然而,当应变足够大时,即使是韧性金属也会断裂,这是材料加工硬化的结果,使其变得脆性。热处理如退火可以恢复工件的延展性,从而可以继续成形。 | |||
====流塑性理论==== | |||
流动塑性是一种固体力学理论,用于描述材料的塑性行为。 流动塑性理论的特点是假设存在流动规则,可用于确定材料的塑性变形量。在流动塑性理论中,假定物体的总应变可加(或乘)分解为弹性部分和塑性部分。应变的弹性部分可以从线性弹性或超弹性本构模型中计算出来。然而,确定应变的塑性部分需要流动规律和硬化模型。 | |||
===屈服准则=== | |||
[[File:Stress strain ductile.png|thumb|right|Stress strain]] | |||
如果应力超过一个临界值,材料将发生塑性或不可逆变形。这个临界应力可以是拉伸的,也可以是压缩的。Tresca准则和Huber–von Mises准则通常用于确定材料是否屈服。然而,这些标准已被证明不适用于大量的材料,其他几个屈服标准也在广泛使用。 | |||
====Tresca准则==== | |||
Tresca准则基于这样一个概念:当材料发生剪切变形时,它会发生剪切破坏,当考虑金属时,这是一个相对好的假设。给定主应力状态,我们可以使用[[wikipedia:Mohr's circle|莫尔圆]]来求解材料将经历的最大剪应力,并得出结论,材料将会屈服如果: | |||
: <math>\sigma_1 - \sigma_3 \ge \sigma_0</math> | |||
这里''σ''<sub>1</sub>是最大正应力, ''σ''<sub>3</sub> 是最小正应力, ''σ''<sub>0</sub> 是材料在单轴载荷下失效的应力。 [[wikipedia:yield surface|屈服面]]可以被构造用于提供这个概念的视觉表示。在屈服面内部,变形是弹性的。从表面上看,变形是塑性的。材料在其屈服面之外不可能有应力状态。 | |||
[[File:固力3.png|thumb|right|固体理论变形理论|600px]] | |||
====Huber–von Mises准则==== | |||
Huber-von Mises准则<ref>{{cite journal |last=von Mises |first=R. |year=1913 |title=Mechanik der festen Körper im plastisch-deformablen Zustand |journal=Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen |series=Mathematisch-Physikalische Klasse |volume=1913 |issue=1 |pages=582–592 |url=http://www.digizeitschriften.de/dms/resolveppn/?PID=GDZPPN002503697 }}</ref> 基于Tresca准则并考虑了流体静应力不会导致材料失效的假设。 [[wikipedia:Tytus Maksymilian Huber|M. T. Huber]] 是第一个提出'''剪切能'''判据的人。<ref>{{cite journal |last=Huber |first=M. T. |title=Właściwa praca odkształcenia jako miara wytezenia materiału |journal=Czasopismo Techniczne |location=Lwów |year=1904 |volume=22 }}翻译为 {{cite journal |title=Specific Work of Strain as a Measure of Material Effort |journal=Archives of Mechanics |volume=56 |pages=173–190 |year=2004 |url=http://am.ippt.pan.pl/am/article/viewFile/v56p173/pdf }}</ref><ref>See {{cite book |first=S. P. |last=Timoshenko |title=History of Strength of Materials |location=New York |publisher=McGraw-Hill |year=1953 |page=369 |url=https://books.google.com/books?id=tkScQmyhsb8C&pg=PA369 |isbn=9780486611877 }}</ref> | |||
Von Mises求出了单轴加载下的[[wikipedia:effective stress|有效应力]],减去静水应力,并指出,所有大于导致材料在单轴加载下失效的有效应力都会导致塑性变形。 | |||
: <math>\sigma_v^2 = \tfrac{1}{2}[(\sigma_{11} - \sigma_{22})^2 + (\sigma_{22} - \sigma_{33})^2 + (\sigma_{11} - \sigma_{33})^2 + 6(\sigma_{23}^2 + \sigma_{31}^2 + \sigma_{12}^2)]</math> | |||
同样,可以使用上面的方程构建屈服面的可视化表示,该方程的形状为椭圆。在表面内部,材料发生弹性变形。到达表面意味着材料经历塑性变形。 | |||
{{#ev:youtube|https://www.youtube.com/watch?v=xkbQnBAOFEg|500px}} | |||
该视频简介了若干种屈服理论。 | |||
==固体力学的现代发展 == | |||
[[File:固力1.png|thumb|right|固体力学在航天中的应用]] | |||
经过几百年的迅速发展,固体力学的知识体系和研究方法都已经逐渐丰富,弹性理论和塑性理论两大范式的发展为固体力学奠定了坚实的基础。但随着现代工业的迅速发展,后工业时期出现了很多的工程问题和新的需求是已有的范式无法解决的,这也催生了固体力学更多新范式的产生。其中具有代表性的就是断裂力学和复合材料力学两大范式。 | |||
===断裂力学=== | |||
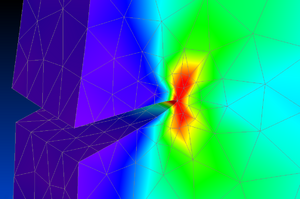
[[File:Color Contour.png|right|thumb|fracture mechanics]] | |||
随着大工业 技术的发展,航空、船舶、容器和管道中部件的断裂频繁发生,传统的强度理论和已有的范式已难于满足现代结构和材料的设计要求以达到安全经济的目的<ref> 余寿文. 断裂力学的历史发展与思考[C]. 中国力学学会力学史与方法论专业委员会.第七届全国力学史与方法论学术研讨会力学与实践专刊.中国力学学会力学史与方法论专业委员会:中国力学学会,2015:106-110. </ref>。断裂力学就在这样的背景下诞生。断裂力学是固体力学在现代发展的一个重要范式,研究含裂纹型缺陷的物体的强度和裂纹扩展的规律。断裂力学的研究内容包括:用力学的理论与方法探求描述主导裂纹起裂与扩展的力学参量;确定材料抵抗裂纹扩展能力的指标和上述二者的联系——断裂准则<ref> 余寿文. 断裂力学的历史发展与思考[C]. 中国力学学会力学史与方法论专业委员会.第七届全国力学史与方法论学术研讨会力学与实践专刊.中国力学学会力学史与方法论专业委员会:中国力学学会,2015:106-110. </ref>。 | |||
断裂力学有三个经典的研究内容,即:线弹性断裂力学、弹塑性断裂力学和断裂动力学<ref>康颖安.断裂力学的发展与研究现状[J].湖南工程学院学报(自然科学版),2006(01):39-42.</ref>。 | |||
断裂力学范式理论的建立和完善主要由以下科学家及其研究成果完成:1920年,[[wikipedia:Alan Arnold Griffith|格里菲斯]]发表了他那篇著名的论文:''The phenomenon of rupture and flow in solids''。该文次年刊登在皇家学会的''Philosophical Transactions''杂志上<ref>Griffith, Alan Arnold. "VI. The phenomena of rupture and flow in solids." Philosophical transactions of the royal society of london. Series A, containing papers of a mathematical or physical character 221.582-593 (1921): 163-198.</ref>。他认为,材料内部有很多显微裂纹,并从能量平衡出发得出了裂纹扩展的判据,一举奠定了断裂力学的基石;紧接着1921年,格里菲斯在研究玻璃断裂问题时提出了能量释放率准则,更完善了断裂力学的基础。[[wikipedia:George Rankine Irwin|欧文]]在1955年和1957年分别提出了裂纹尖端应力应变场实用公式和应力强度因子的断裂准则,和格里菲斯的成果共同组成了线弹性断裂力学的主体。1960年[[wikipedia:Grigory Barenblatt|Barenblatt]]建立了内聚区断裂模型,威尔斯提出了裂纹张开位移作为韧性断裂的控制参量,1965年威尔斯得出弹塑性条件的断裂准则,也成为了弹塑性断裂力学的重要突破。断裂动力学的发展则主要是70年代初Sith和洛依伯研究的外载随时间变化而裂纹是稳定情况的渐进应力场和位移场,以及瑞斯等人先后导出的裂纹以等速传播情况的渐进应力场和位移场。 | |||
断裂力学的范式变化主要经历了从研究含有裂纹型缺陷的固体力学问题及其工程应用到研究缺陷的成因和演化以及如何用数学物理的语言定量描述两个阶段。但是一些前沿工程应用上出现的问题,诸如诸如能源 (油气) 中的油气压裂、页岩气开采、智能制造的传感致动机构的失效、交通运输(如高铁、航空)中的断裂疲劳问题、保健康复中的器件失效与可靠性问题,地震与地质和自然界破裂运动等等据需要进一步的发展。 | |||
===复合材料力学=== | |||
[[File:Composite-materials-technology.jpg|thumb|left]] | |||
工程上固体材料的应用,除了需要考虑含裂纹缺陷型材料的性质,寻找一种具有优良力学性质的复合材料也是突破口之一,这也催发了现代固体力学里面另一个重要范式的发展——复合材料力学。在固体力学的研究中,现代固体力学面临的最活跃和变化多端的就是对固体材料的多样性力学行为认识<ref>余寿文. 现代固体力学研究范畴的讨论——固体力学史与方法论的注记之二[C]. 中国力学学会力学史与方法论专业委员会.第三届全国力学史与方法论学术研讨会论文集.中国力学学会力学史与方法论专业委员会:中国力学学会力学史与方法论专业委员会,2007:32-38.</ref>。复合材料力学的研究进展与复合材料的广泛应用紧密相关,成为了我们研发复合材料和研究某种复合材料的性质和应用情况的重要依据。 | |||
复合材料力学主要致力于从微观和宏观两个方面研究复合材料的力学性质,近代复合材料最重要的有两类:一类是纤维增强复合材料,主要是长纤维铺层复合材料,如玻璃钢;另一类是粒子增强复合材料,如建筑工程中广泛应用的混凝土等<ref>严锐.复合材料力学综述[J].工程与建设,2017,31(02):159-161</ref>。 | |||
复合材料力学的范式发展和断裂力学有着显著的不同,其并没有明显的发展脉络和理论成果的发展时间等,但其具有较强的横向发展的特征。随着现代技术和实际需求的不断更替,复合材料力学中,诸如陶瓷纳米复合材料力学问题,碳纳米管聚合物复合材料力学问题,纤维增强树脂基复合材料力学问题等,都是这一范式的重要组成部分。 | |||
随着科技的不断进步,固体力学在近现代都有了很大程度的范式发展。断裂力学是包含了众多固体材料裂纹缺陷以及从而解决其引发工程问题的固体力学范式,而复合材料力学则是推动了复合材料学的重要理论范式。随着解决新问题的需求的变化,现代固体力学的范式逐渐面面临了危机,而逐渐发展起来的计算力学、损伤力学、生物力学等新的范式,都仍然需要更多科学家们的努力。 | |||
===待解决的问题——不可通约性([[Incommensurability]])=== | |||
====[[wikipedia:Multiscale modeling|多尺度 (multi-scale) 模拟]]==== | |||
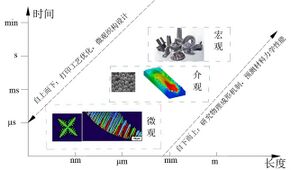
[[File:Scale.png|thumb|right|Multi-scale phenomenona]] | |||
现在有关断裂,疲劳以及裂纹问题的高阶固体力学发展已经不局限于'''宏观''' (macro-scale) 层面了,或者说宏观固体力学发展已经相对成熟,突破不大。然而从材料微观 (micro-scale) 的细小缺陷开始进行模拟的'''微观力学''' (micro-mechanics) 是发展的一个方向。微观力学结合宏观力学的材料力学模拟就称为多尺度(multi-scale)固体力学,这是将来一个热点问题。 | |||
[[File:多尺度.jpg|thumb|left|多尺度力学]] | |||
很多我们直觉的想法一旦到了微观领域都改变了,比如'''尺寸效应'''。为了得到相应的微观模型参数,实验是不可少的。右图就是在某型号钢材微观拉长实验中,孔洞在拉长之后的变形情况。而材料种类有很多,由此学科诞生的各种实验确定模型参数的工作量是巨大的 (有点偏材料学了)。任何宏观系统的表现形态,都是微观粒子个体行为集成的宏观表现:即宏观系统如何(How)表现,为什么(Why)如此表现,其根本是宏观系统的每一个粒子处于(What)什么微观状态(由'''量子力学'''的原理,我们无法考察每个微观粒子如何(How)运动,但对于粒子的关键特征,如什么(What,实际是量子化的Which)能量状态,我们可以用What来刻画)。这一部分可与[[于舒昂 Final Project|量子力学]]的学科范式产生紧密的联系。 | |||
多尺度力学方法需要以材料的微观结构信息为基础,目前能够从微观尺度上对材料进行力学分析的方法有'''第一性原理'''、'''分子动力学''' ([[wikipedia: Molecular dynamics|Molecular dynamics]], MD)、晶体塑性力学方法等。其中,MD方法是基于原子间相互作用的微观模拟方法,以其能够给出微观结构的动态演化信息从而能够分析大量微观机制而被广泛应用。尽管 MD 方法在时空尺度上存在一定的局限性,但大量研究表明,MD 的模拟结果能够清晰地阐明材料的变形和破坏机制,为跨尺度力学分析奠定重要的物理基础。晶体塑性力学是基于晶体位错滑移理论的一种连续介质力学方法,其可以从底层微结构信息出发,分析材料的宏观力学行为。近年来,以晶体塑性理论为基础的多尺度力学模型随着计算机模拟技术的发展,在结构完整性分析中得到越来越广泛的应用。理机制分析指导结构件的力学性能优化。 | |||
现如今,研究各类固体材料力学行为的宏微观理论计算方法越来越丰富,然而,不同尺度下的计算方法所得到的材料力学性质会有一定的差异,如何发展宏微观下多尺度统一的力学方法是一个非常具有挑战性的课题。另一方面,数据技术驱动的人工智能方法发展迅速,这为人们提供了一种全新的'''数据驱动'''的(data-driven)力学研究方法。基于微观模拟或试验得到的微观物理信息数据库,采用[[wikipedia: deep learning|深度学习]]的方法进行数据训练,更高效地开发新的力学模型,对于实际工程应用中的结构完整性问题给出快速可靠的分析结果。 | |||
====[[wikipedia:Nonlinear system|非线性]]耦合 (nonlinear coupled)==== | |||
[[File:Fig.png|thumb|right|Why is a special form of What]] | |||
在固体力学理论已经成熟的情况下,如何高效实现这些理论也是一个热点。比如非线性耦合问题就出现在很多高级固体力学模型中,具体体现为在实现过程中要求解很多相互耦合的高阶非线性问题。这些求解过程在基于有限元的计算力学很多都是无法实现的或者计算时间太长 (每个高斯积分点都要求解)。因此如何把强耦合 (strongly coupled) 的问题化简为非耦合 (Decoupled) 或者弱耦合 (weakly-coupled) 的问题,使得实现过程相对简单,也是一个热点问题。 | |||
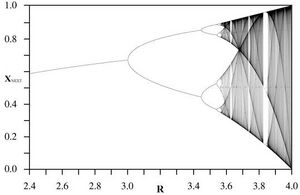
[[File:Chaos.jpg|thumb|left|非线性动力学实例:logistic chaos]] | |||
非线性力学是非线性科学的一个重要分支,它曾经也将持续对非线性科学的发展起积极的推动作用,多体问题、Stokes波、Riemann问题都是典型的例子,上世纪60年代发现的孤立子和混沌也有其力学背景,这两个事件是非线性科学形成的里程碑。非线性力学,尤其是固体力学,侧重于研究固体物质机械运动中的非线性现象。 | |||
'''非线性'''问题,即'''叠加原理'''不再适用的一大类问题,基于这一原因,原来适用于数学物理中的各类线性方程的方法如:分离变量、积分变换、Green函数等统统失效。目前已发展出摄动法、速度图法、李群变换(包括相似性解)、反演散射法等一系列针对非线性问题的有效解法,但都不具有普适性,只对非线性问题中的少数特例起作用。目前,非线性计算稳定性、谱方法、自由边界问题、有限自由度系统等问题,是非线性问题中亟待解决的若干难点。 | |||
非线性问题解法的发展离不开计算技术的发展,'''符号计算'''([[wikipedia:symbolic computation|symbolic computation]])和'''并行计算'''([[wikipedia:parallel computing |parallel computing]])将成为非线性问题计算的新范式,而'''符号计算'''下的非线性问题系统的描述,其本身就是一个'''偏序集'''。由于符号计算消除了有限步之内的数值误差,使其计算过程具有自反性,反对称性与传递性。'''并行计算'''下的非线性系统,其描述也是'''对称破缺'''的,非线性系统本身引起的非对称性,和剖分并行在处理方法上引入的对称性,为我们认识并解决非线性问题提供了新的视角和方法。 | |||
==结论== | |||
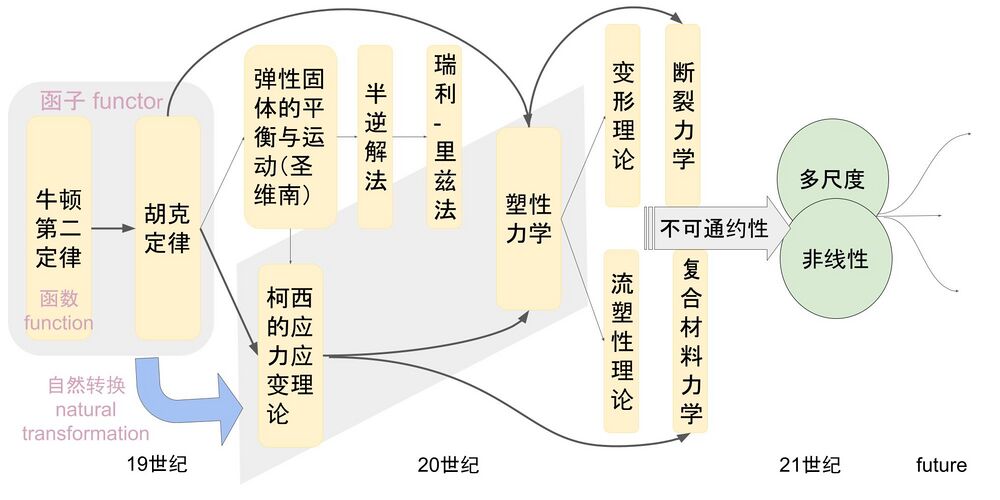
固体力学发展近四百年的历史中范式转换的过程,可以用'''范畴论'''中的'''态射'''进行刻画,(一个范式内:问题→解决方案的关系是'''函数''';从A范式到B范式之间的映射是'''函子''';而AB范式转换→BC范式转换两过程的比较是'''自然转换'''),整个范式转换的过程构成了'''偏序集'''的数据结构,它是没有回圈的。在每个范式的'''科学共同体'''中,科学家的语言构成了该范式的'''命名空间''',随着范式的转化,'''命名空间'''也会有所改变。由于每隔一段时间在学科发展中出现的反常,固体力学的发展会在不同范式之间出现'''对称破缺''',即所谓的'''不可通约性'''。当固体力学问题与其他学科发生交叉时,不同范式之间发生'''超链接'''。不可通约性在目前固体力学的前沿发展中主要体现在以下两个待解决的问题中——即'''多尺度'''问题和'''非线性'''问题,由上文所述,'''多尺度'''本身就具备良好的'''偏序'''结构(尺度上的传递性有序结构),而'''非线性'''系统是'''对称破缺'''的(物理系统所满足的规律具有某种对称性,但是系统本身不具有这种对称性),对这两个问题的认识将决定未来固体力学学科范式的发展走向。 | |||
[[File:Figend.jpg|1000px|thumb|center|结语]] | |||
=References= | |||
<references/> | |||
[[Category:TDCF2021]] | |||
{{#set: | |||
Has Topic={{PAGENAME}} | |||
|Author=李欣荣 | |||
}} | |||
Latest revision as of 06:24, 9 February 2022
对科学革命、范式、科学共同体的再思考
《科学革命的结构》(The Structure of Scientific Revolutions),1962年出版;于1970年再版;英文简写为SSR),是美国科学史家与科学哲学家托马斯·库恩(Thomas Samuel Kuhn)的著作。这本书的出版是历史,哲学和科学知识社会学的一个里程碑事件;在学术界内外,引发了连续广泛的评估和反响。库恩挑战当时对“常态科学”历程的主流观点。常态科学的历程被认为是由公认事实和理论“累积而发展”,而他认为:相对于常态科学这样累积连续概念的期间中,另外有一段被革新科学所中断的模式。在科学革新历程中发现的“异常现象”导出了新的范式,然后以此范例质疑旧数据的新问题,超过之前范式单纯的“解谜”,改变研究规则并指导新研究的“地图”。
托马斯·库恩在其著作《科学革命的结构》(以下简称《结构》)中系统地、独创性地对科学演进的过程进行了总结,并提出了影响深远的“范式”概念。《结构》将“范式”定义为:“某些实际科学实践的公认范例——包括定律、理论、应用和仪器”[1],而这种“公认范例”可以为特定的连贯的科学研究的传统提供模型。于是,科学演进的过程可以概括为:由建立在特定范式之上的“解谜”的常规科学,到出现既有范式无法解释或应对的反常,再到随反常现象而来的“显著的专业不安全感”从而引发危机,最终通过范式转换的方式完成科学革命,旧范式全部或部分地被一个与其完全不能并立的崭新范式所取代。这一概括以及背后的细节对科学工作者更好地认识科学发展以及在科学中自我定位起到了重要的参考和指导作用。
本文将结合《超越学科的认知基础》的课程,探讨以下三方面的内容:科学革命的过程与前后的科学知觉转变、新时期学科交叉环境下的科学范式、人在科学中扮演的角色以及行为准则。以上三条内容是基于《结构》中重要的概念:科学革命、范式、科学共同体的再思考。前两者聚焦于科学发展的历程,而后者聚焦于科学工作者在科学发展中的作用以及受到的影响。本文旨在从科学自身的发展和科学的参与者这两方面提出新的思考。 {{#ev:youtube|https://www.youtube.com/watch?v=L70T4pQv7P8%7C500px}} 该视频简介了《科学革命的结构》与作者托马斯·库恩。
科学革命与科学知觉的转换 & 态射( Morphism)
科学演进的过程中伴随着科学知觉的转换 Cite error: Invalid <ref> tag; invalid names, e.g. too many,尤其体现为科学共同体集体或其中有卓越贡献的个人的思维方式的变化,并且常规科学与渐进式的思维演变、科学革命与思维的跳跃往往有着良好的对应关系,如:《结构》中提到的天文学范式转变、王训教授讲座中提到的赵忠贤院士将铁基超导体的临界温度提升至超过麦克米兰极限,都是思维跳跃带来科学突破的范例。而另一方面,科学的演进,尤其是范式转换,也可以带来包括思维方式在内的科学知觉的转变,并且这种转变几乎内化为新范式的一部分。库恩强调:“科学接受一个新范式之后,将产生视觉的、知觉的及其他心理的转变,已至会以与以前不一样的方式来看这个世界,也可以说,生活于或工作于一个新的世界中Cite error: Invalid <ref> tag; invalid names, e.g. too many。例如《结构》中提到的:化学范式转变后,新范式下的化学家“在一个不同的世界里工作” Cite error: Invalid <ref> tag; invalid names, e.g. too many,足以体现科学知觉发生的颠覆性变化。
对于今天的人类是否面对着新一轮的颠覆性科学革命,学界普遍的观点是:目前人类正处于第二次工业革命和石油世纪的最后阶段[2]。而这是一个令人难以接受的严峻事实,因为这一现实将迫使人类迅速过渡到一个全新的能源体制和工业模式,而新的工业革命和经济革命必然以科学革命作为先导。而纵观当下世界,信息时代的全球信息的联通与共享、以及可再生能源发展初见成效,不难预见新的通讯技术与能源系统结合之际,即将来临的科学革命的基本样貌。
回顾自然科学发展的历史,其科学方法论从宏观来说主要由整体论和还原论这两种方法论体系构成,而整体论又随着西方科学的进步,特别是分析、还原科学的兴起而走向衰落[3]。随着牛顿力学的巨大成功,还原论被近代科学视为一种万能的科学方法论用于刻画世界,并且取得了辉煌的成就。直到二十世纪90年代,基于超越还原论的复杂性科学逐渐兴起,沉寂千年的整体论也随着复杂性科学而逐渐复兴。在这场变革中,大数据技术和互联网技术以及背后蕴含的全新思维方式,发挥着相当重要的作用。《大数据时代》的作者舍恩伯格认为:“大数据开启了一次重大的时代转型,而大数据时代的变革首先是思维变革,继而影响商业变革和管理变革”[4]。同时他也指出了这种思维转变的核心特点:放弃对因果关系的渴求,而取而代之关注相关关系,即只需知道“是什么”而不去关注“为什么”。这恰恰颠覆了千百年来人类的思维惯性,具体还体现在:不关注随机样本,而是关注全体数据;不要求精确性,而是追求混杂性等等。由于大数据技术处理了所涉及问题的全部数据,这就使得整体论中全面、完整把握对象的思想有了完整的体现和科学的表述,而另一方面,对一个个具体数据的处理也部分应用了还原论中的方法。这也与过去科学中追求统一化、标准化的科学逻辑不同,人们无需再将问题在理论层面进行简化,把复杂、多样的东西首先通过还原论还原到一个基点,从而更加有助于科学工作者接近事实的真相。从科学方法论以及科学知觉转变的角度来说,即将到来的科学革命甚至要比以往任何科学革命来得更加彻底、有更深远的影响。
范畴论: 范畴代表着其他数学概念的抽象表示。 许多数学领域都可以被归化为范畴论中的范畴。因此,范畴论使用抽象来使陈述和证明复杂而微妙的数学结果以更简单的方式呈现。
态射:在数学尤其是范畴论中,态射是一种保持结构的映射,它从一个数学结构到另一个相同类型的数学结构。态射的概念在当代数学中多次出现。在集合论中,态射是函数;在线性代数中,线性变换;在群论中,群同态;在拓扑学中,连续函数等等。
该视频简介了抽象代数与范畴论中的基本概念,对于理解下文具有直接帮助。 {{#ev:youtube|https://www.youtube.com/watch?v=XPF5fe1WdKY%7C500px}}
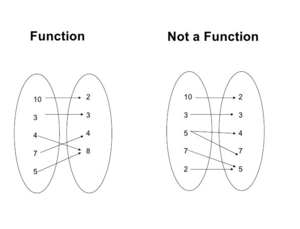
函数(function)定义:
In 数学中,从 X集合到 Y集合的函数是Y 集合中的元素与X集合中的任一元素的对应关系。集合X称为 函数的定义域 ,集合 Y 称为函数的值域。
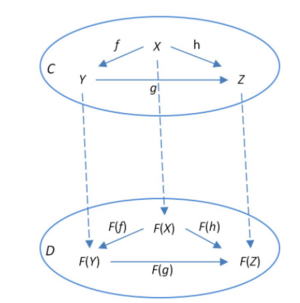
函子(functor)定义:
Let C and D be categories. A functor F from C to D is a mapping that:
- associates each object in C to an object in D,
- associates each morphism in C to a morphism in D such that the following two conditions hold:
- for every object in C,
- for all morphisms and in C.
自然转换(natural transformation)定义:
If and are functors between the categories and , then a natural transformation from to is a family of morphisms that satisfies two requirements.
- The natural transformation must associate, to every object in , a morphism between objects of . The morphism is called the component of at .
- Components must be such that for every morphism in we have:
If both and are contravariant, the vertical arrows in this diagram are reversed. If is a natural transformation from to , we also write or . This is also expressed by saying the family of morphisms is natural in .
If, for every object in , the morphism is an isomorphism in , then is said to be a natural isomorphism (or sometimes natural equivalence or isomorphism of functors). Two functors and are called naturally isomorphic or simply isomorphic if there exists a natural isomorphism from to .
An infranatural transformation from to is simply a family of morphisms , for all in . Thus a natural transformation is an infranatural transformation for which for every morphism . The naturalizer of , nat, is the largest subcategory of containing all the objects of on which restricts to a natural transformation.
学科交叉与范式 & 超链接
上世纪后半叶起,新兴科学越发呈现出多学科交叉、综合的特点,这一定程度上也源于常规科学遇到的瓶颈。进入21世纪,交叉学科的迅猛发展正在为科学创新注入新的活力,也体现出科学向综合性发展的趋势。上至生物信息学、计算化学等已经初具规模的新型学科,下至迅速转化交叉学科科研成果的工程应用,如智能硬件、纳米材料等等,学科交叉带来的创造力可见一斑。在2020年听过的姚期智教授的一次讲座中,他由自己从物理学研究转向当时新兴的计算机科学研究的个人经历,说明了多学科知识储备对于学术研究的重要作用。物理方面深厚的专业基础,使他在进入量子计算的全新领域时可以游刃有余,不会过多地理论学习所困扰。而其引领的量子计算领域,相比传统计算在效率方面有巨大的飞跃,充分体现出学科交叉的强大能量。姚先生的经历也启示着未来从事科研的科学工作者,广泛涉猎各学科的知识,从而在学科交叉点发现更多创新的基点。而姚期智院士的讲座中曾介绍一代大师阿兰·图灵的介绍,亦体现出学科交叉与多学科知识储备的重要性。图灵先生青年时期接受的宽口径自然科学教育使得他可以在人工智能和数理生物学等多学科领域取得颠覆性的成就。
交叉学科的范式,相较于传统学科的范式,或许具有更多的进步性特征。由于它承载于众多学科的底层逻辑之上,而每个学科发生的反常,都会对交叉学科产生直接影响。因此,交叉学科更容易通过各种反常情形发现完善范式的方向。而另一方面,由于各学科的相互牵制,在一定程度上,交叉学科的范式转换更难完成。如果仅有底层学科其中之一的理论飞跃,则难以使交叉学科的范式产生革命性的发展。交叉学科范式转换应该是底层学科范式联动转换,全面进步的结果。
库恩的理论在学科交叉的情景下有很大的不适用性,于舒昂同学在于舒昂 感悟一节中指出了库恩理论的一些时代局限性。库恩的理论阐述了:“一个科学工作者只能属于一个特定的科学共同体”,但这在如今学科交叉广泛存在的科学界是不切实际的。
Paradigm: 在科学和哲学中, 范式 (Paradigm,/ˈpærədaɪm/) 是一组不同的概念或思维模式,包括理论、研究方法、假设和标准,这些标准构成了一个领域的贡献。
“人”的科学与科学共同体 & 命名空间(Namespace)
科学归根结底是“人”的科学,它是人类文明的产物。库恩在《结构》中也提及了很多关于人与科学关系的内容:“在范式确立前的科学模式中,科学团体缺乏共同的研究信念,不同研究者的工作要从奠基做起,选取的方法与支撑理论个人色彩强烈,科学工作者的著作多与其他学派的成员进行对话”Cite error: Invalid <ref> tag; invalid names, e.g. too many;又如:“科学的改宗往往会受到很多非科学因素的影响,而其本质是社会中的人的影响”。《结构》中还界定了“科学共同体”的概念:“一个科学共同体由同一个科学专业领域的工作者组成,他们受到近似的教育和专业训练,研究过相似的界定该科学学科界限的文献”Cite error: Invalid <ref> tag; invalid names, e.g. too many。从而,常规科学和科学革命都在科学共同体的活动的基础上展开,范式的概念也紧紧依附于科学共同体,库恩称其为:科学共同体“团体承诺的集合”、“共有的范例”。
朱邦芬教授的讲座中提到了一些学术共同体对其成员科学研究产生影响的例子,如:黄昆先生从黄方程的建立,极化激元概念的提出,到多声子跃迁理论的开创,其中反映出一个好的研究群体对其中个体成员发现和提出好的研究问题的启示作用;以及学术共同体的传承中,导师或前辈对后来者的影响集中体现在思维风格,而非简单的知识传授。又以居里夫人为例,说明了个人的品格对其学术成就的影响。同时指出:“创造知识方面的缺陷往往源自学习知识时的一些问题,也受限于人格的养成。”由此,可以更加深刻地认识通识教育的意义,通识教育所培养的独立思考和判断的能力,对于未来的科学研究具有重要的影响。如爱因斯坦所说:“青年人在离开学校时,是作为一个和谐的人,而不是作为一个专家。”
现代科学的两大基石:形式逻辑推理和实验检验均基于求真的要求并保证结论趋近于真实,因此,人作为科学的主体,必须有可以凭借的事物以限制所从事的科学的严谨与规范,于是,在不同的科学共同体中形成了相应的学术规范与判断准则。在严格的规范框架下,对自然运行的个体观察才可以呈现给他人,并被他人独立判断其有效性之后转换为科学共同体的学术共识。因此,良好的学术环境应该具有这一特点:驱使科学工作者维护科研诚信并重视自己及团队的学术声誉。
命名空间: 在计算中,命名空间(namespace)是一组符号(名称),用于识别和引用各种类型的对象。命名空间确保给定的所有对象都有唯一的名称,以便容易识别它们。 命名空间的结构通常为层次结构,以允许在不同上下文中重用名称。作为一个类比,考虑一个命名系统,其中每个人都有一个名字,以及与他们的亲戚共享的姓氏。如果家庭成员的名字只在每个家庭中是唯一的,那么每个人都可以通过名字和姓氏的组合来唯一地识别;只有一个无名氏,虽然可能有很多叫Jane的人。在Doe家族的名称空间中,仅仅“Jane”就足以明确地指定这个人,而在“全局”的命名空间中,必须使用全名才有可能确认到个体。
学科演进的例子:固体力学
该视频简介了固体力学的发展史、基本假设及基本概念。 {{#ev:youtube|https:/https://www.youtube.com/watch?v=d9AbPLAwKaI%7C1200px%7Ccenter}}
弹性力学(Elastic mechanics/Elasticity)
“胡克定律”
弹性理论范式形成初期的工作是通过实践、探索弹性力学的基本规律。1678年,英国科学家胡克(Robert Hooke)在他的著名论文《恢复原形的或弹簧的势能》中用拉丁文“Ut tension sic vis” 首次阐述了“任何弹簧的力与它的伸长按同一比例增加,即力与变形成正比关系”的规律。 胡克提出该定律的过程颇有趣味,他于1676年发表了一句拉丁字谜,谜面是:ceiiinosssttuv。两年后他公布了谜底是:ut tensio sic vis,意思是“力如伸长那样变化”紧接着,1680年,法国科学家马略特(Edme Mariotte)又独立地发现了这一定律,二人分别对自己的发现进行了大量的实验验证。在随后的三百多年中,弹性力学的几乎一切工作都在胡克定律的基础上展开:
值得一提的是,早在胡克之前,我国东汉时期的学者郑玄既提出过类似的规律。他在注释《考工记·弓人》中“量其力,有三均”这句话时,记录了以下文字:“假令弓力胜三石,引之中三尺,驰其弦,以绳缓擐之,一石,则张一尺”。这里的文字展示了古代中国人测量弓弩的刚度时所发现的“力与伸长成正比”的定律。然而,长久以来,这一规律仅仅作为生产生活中检验、制造的经验规则,并没有被人们深入地探究及验证,没有成为真正意义上的科学。
即使十七世纪的胡克定律,也存在着一定的瑕疵。例如:1691年,在莱布尼兹(Gottfried Wilhelm Leibniz)和惠根斯(Christiaan Huyghens)的通信中,惠根斯透露其在重复胡克的实验时,仅当弹簧轻微伸长时,实验结果才与理论一致。事实上,最初的胡克定律未能注意到这种简单线性关系的适用范围问题,对于大变形或者塑性变形等各种几何非线性和材料非线性情况,力与变形便不再是正比关系。反常的出现,使得弹性理论范式不断被完善、发展。
柯西和纳维的奠基性工作
自胡克之后,越来越多的科学家开始尝试建立研究弹性体问题的通用理论架构。这一阶段,人们还是主要使用粗糙的、不完备的理论来处理简单构建的力学问题,其中欧拉(Leonhard Euler)、伯努利(Daniel Bernoulli)等人的工作取得了一定的突破,尤其在关于梁、板的理论方面。同时,数学工具的发展,使得建立弹性力学数学理论的条件已大体具备。十九世纪20年代,纳维(Navier)和柯西(Cauchy)的工作,完整地建立了弹性力学范式的数学理论大厦。
1821年,纳维向法国科学院提交了他的论文《弹性固体的平衡定理与运动的研究报告》,在弹性体的分子理论上有了更进一步的成就,在纳维推导出的各向同性弹性体的平衡微分方程中,利用他提出的假设来求物体的弹性仅需一个常数即可。随后,柯西综合了纳维的推导并研究了各项异性的弹性体,并指出:在最普遍的情况下,要决定物体的弹性需要15个常数。柯西更大的贡献在于他借鉴水力学中平面上压力的概念,引入了应变和应力,以代替个别质点间分子力的研讨。柯西本人利用这套理论研究过矩形杆件的变形,也为后来圣维南(Adhémar Jean Claude Barré de Saint-Venant)推导出完整的棱柱杆扭转理论建立了基础。
柯西在1822~1828年发表的几篇论文中,明确了如应力(Stress),应变(Strain),应力分量,应变分量等一系列概念,建立了弹性力学的几何方程、平衡方程、各向同性以及各向异性材料的广义胡克定律,从而打开了弹性力学向纵深发展的突破口。
线性各向同性弹性力学大发展
19世纪中叶,圣维南运用弹性力学的基本方程和他自创的半逆解法([semi-inverse method]),奠定了柱体扭转理论研究的基础,也标志着线性各向同性弹性理论大发展时期的到来。利用半逆解法,只需假定位移和力的一些特征,就可以推断出这些量的其余特征使其能满足所有的弹性方程,并且运用该方法得到的理论结果与实验结果密切吻合,因此他本人断言:“凡是学过基本材料力学近似解的工程师都能用这个方法得出有实用价值的精确解来”。圣维南为弹性理论范式的完善做出了卓越的贡献,以至于在托德亨特(Todhunter)与皮尔逊(Karl Pearson)合著的《弹性力学史》的扉页上,都写有“为了纪念近代最先进的弹性学家圣维南,编者谨以编著此书的劳力奉献给他”的献词。
在随后的几十年中,1881年,德国科学家赫兹(Heinrich Rudolf Hertz)解决了两弹性体局部接触时弹性体内的应力分布问题,1898年,基尔施(Kirsch)发现了应力集中现象……诸多理论突破解释了过去一些反常的实验现象,同时,新的理论也广泛地运用于解决工程问题,弹性力学得到了工程界的重视,在提高机械、结构等零件设计水平方面起了重要作用。
这一时期的标志性特征还有:发展了许多有效的近似计算、数值计算方法,例如著名的“瑞利-里兹法”。这一方法于1877年,由英国科学家瑞利(John William Strutt)在《声学理论》中首先使用,随后又被瑞士科学家里兹(Ritz)于1908年作为一种有效方法提出,它不光大大提高了弹性理论解决实际工程问题的能力,同时也推动了物理等其他相关学科中近似计算的蓬勃发展。
弹性理论的全新机遇
20世纪后,弹性力学的经典理论仍在不断完善,同时也被科学家作为探讨许多复杂问题的有效工具,出现了相关联的边缘范式和交叉范式。例如:考虑温度影响的热弹性力学,研究固体同气体、液体相互作用的气动弹性力学、水弹性力学,以及适用范围更广的各向异性和非均匀体的理论,非线性弹性力学等等。不同学科的紧密配合与联系正在为弹性力学的发展注入新的活力,这些新领域的发展,亦将直接促进相关工程技术的进步。
塑性力学(Plastic mechanics/Plasticity)
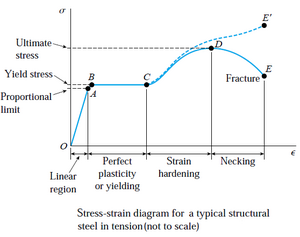
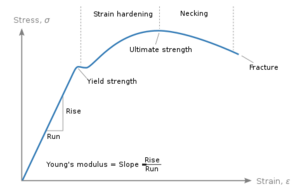
塑性力学的本质是一种用来描述材料的塑性行为的理论。一旦材料发生塑性行为,材料的应力应变关系不再是线弹性的,这个时候就需要新的数学描述,这套基于材料塑性行为发展而来的理论就是塑性力学,其与弹性最大的区别就是存在不可恢复的塑性变形。
上式表明,如果我们知道了应变和塑性应变,我们就可以知道这一点的应力,而在弹性力学中我们仅仅需要知道应变就可以知道一点的应力。于是乎,一种标准的用来描述这种情形的框架被提了出来,这套框架明确回答了:塑性会在何时发生的问题(屈服函数),塑性发生时塑性应变的变化(流动法则),塑性变形时材料强化的问题(强化法则)以及其他补充的条件。
数学描述
变形理论
塑性力学有若干种数学描述,其中一种是变形理论(如胡克定律):柯西应力张量(d-1阶)是应变张量的函数。虽然当一小部分物质受到不断增加的载荷(如应变载荷)时,这种描述是准确的,但这一理论不能解释不可逆性。韧性材料可以承受较大的塑性变形而不断裂。然而,当应变足够大时,即使是韧性金属也会断裂,这是材料加工硬化的结果,使其变得脆性。热处理如退火可以恢复工件的延展性,从而可以继续成形。
流塑性理论
流动塑性是一种固体力学理论,用于描述材料的塑性行为。 流动塑性理论的特点是假设存在流动规则,可用于确定材料的塑性变形量。在流动塑性理论中,假定物体的总应变可加(或乘)分解为弹性部分和塑性部分。应变的弹性部分可以从线性弹性或超弹性本构模型中计算出来。然而,确定应变的塑性部分需要流动规律和硬化模型。
屈服准则
如果应力超过一个临界值,材料将发生塑性或不可逆变形。这个临界应力可以是拉伸的,也可以是压缩的。Tresca准则和Huber–von Mises准则通常用于确定材料是否屈服。然而,这些标准已被证明不适用于大量的材料,其他几个屈服标准也在广泛使用。
Tresca准则
Tresca准则基于这样一个概念:当材料发生剪切变形时,它会发生剪切破坏,当考虑金属时,这是一个相对好的假设。给定主应力状态,我们可以使用莫尔圆来求解材料将经历的最大剪应力,并得出结论,材料将会屈服如果:
这里σ1是最大正应力, σ3 是最小正应力, σ0 是材料在单轴载荷下失效的应力。 屈服面可以被构造用于提供这个概念的视觉表示。在屈服面内部,变形是弹性的。从表面上看,变形是塑性的。材料在其屈服面之外不可能有应力状态。
Huber–von Mises准则
Huber-von Mises准则[5] 基于Tresca准则并考虑了流体静应力不会导致材料失效的假设。 M. T. Huber 是第一个提出剪切能判据的人。[6][7] Von Mises求出了单轴加载下的有效应力,减去静水应力,并指出,所有大于导致材料在单轴加载下失效的有效应力都会导致塑性变形。
同样,可以使用上面的方程构建屈服面的可视化表示,该方程的形状为椭圆。在表面内部,材料发生弹性变形。到达表面意味着材料经历塑性变形。 {{#ev:youtube|https://www.youtube.com/watch?v=xkbQnBAOFEg%7C500px}} 该视频简介了若干种屈服理论。
固体力学的现代发展
经过几百年的迅速发展,固体力学的知识体系和研究方法都已经逐渐丰富,弹性理论和塑性理论两大范式的发展为固体力学奠定了坚实的基础。但随着现代工业的迅速发展,后工业时期出现了很多的工程问题和新的需求是已有的范式无法解决的,这也催生了固体力学更多新范式的产生。其中具有代表性的就是断裂力学和复合材料力学两大范式。
断裂力学
随着大工业 技术的发展,航空、船舶、容器和管道中部件的断裂频繁发生,传统的强度理论和已有的范式已难于满足现代结构和材料的设计要求以达到安全经济的目的[8]。断裂力学就在这样的背景下诞生。断裂力学是固体力学在现代发展的一个重要范式,研究含裂纹型缺陷的物体的强度和裂纹扩展的规律。断裂力学的研究内容包括:用力学的理论与方法探求描述主导裂纹起裂与扩展的力学参量;确定材料抵抗裂纹扩展能力的指标和上述二者的联系——断裂准则[9]。
断裂力学有三个经典的研究内容,即:线弹性断裂力学、弹塑性断裂力学和断裂动力学[10]。 断裂力学范式理论的建立和完善主要由以下科学家及其研究成果完成:1920年,格里菲斯发表了他那篇著名的论文:The phenomenon of rupture and flow in solids。该文次年刊登在皇家学会的Philosophical Transactions杂志上[11]。他认为,材料内部有很多显微裂纹,并从能量平衡出发得出了裂纹扩展的判据,一举奠定了断裂力学的基石;紧接着1921年,格里菲斯在研究玻璃断裂问题时提出了能量释放率准则,更完善了断裂力学的基础。欧文在1955年和1957年分别提出了裂纹尖端应力应变场实用公式和应力强度因子的断裂准则,和格里菲斯的成果共同组成了线弹性断裂力学的主体。1960年Barenblatt建立了内聚区断裂模型,威尔斯提出了裂纹张开位移作为韧性断裂的控制参量,1965年威尔斯得出弹塑性条件的断裂准则,也成为了弹塑性断裂力学的重要突破。断裂动力学的发展则主要是70年代初Sith和洛依伯研究的外载随时间变化而裂纹是稳定情况的渐进应力场和位移场,以及瑞斯等人先后导出的裂纹以等速传播情况的渐进应力场和位移场。 断裂力学的范式变化主要经历了从研究含有裂纹型缺陷的固体力学问题及其工程应用到研究缺陷的成因和演化以及如何用数学物理的语言定量描述两个阶段。但是一些前沿工程应用上出现的问题,诸如诸如能源 (油气) 中的油气压裂、页岩气开采、智能制造的传感致动机构的失效、交通运输(如高铁、航空)中的断裂疲劳问题、保健康复中的器件失效与可靠性问题,地震与地质和自然界破裂运动等等据需要进一步的发展。
复合材料力学
工程上固体材料的应用,除了需要考虑含裂纹缺陷型材料的性质,寻找一种具有优良力学性质的复合材料也是突破口之一,这也催发了现代固体力学里面另一个重要范式的发展——复合材料力学。在固体力学的研究中,现代固体力学面临的最活跃和变化多端的就是对固体材料的多样性力学行为认识[12]。复合材料力学的研究进展与复合材料的广泛应用紧密相关,成为了我们研发复合材料和研究某种复合材料的性质和应用情况的重要依据。
复合材料力学主要致力于从微观和宏观两个方面研究复合材料的力学性质,近代复合材料最重要的有两类:一类是纤维增强复合材料,主要是长纤维铺层复合材料,如玻璃钢;另一类是粒子增强复合材料,如建筑工程中广泛应用的混凝土等[13]。 复合材料力学的范式发展和断裂力学有着显著的不同,其并没有明显的发展脉络和理论成果的发展时间等,但其具有较强的横向发展的特征。随着现代技术和实际需求的不断更替,复合材料力学中,诸如陶瓷纳米复合材料力学问题,碳纳米管聚合物复合材料力学问题,纤维增强树脂基复合材料力学问题等,都是这一范式的重要组成部分。 随着科技的不断进步,固体力学在近现代都有了很大程度的范式发展。断裂力学是包含了众多固体材料裂纹缺陷以及从而解决其引发工程问题的固体力学范式,而复合材料力学则是推动了复合材料学的重要理论范式。随着解决新问题的需求的变化,现代固体力学的范式逐渐面面临了危机,而逐渐发展起来的计算力学、损伤力学、生物力学等新的范式,都仍然需要更多科学家们的努力。
待解决的问题——不可通约性(Incommensurability)
多尺度 (multi-scale) 模拟
现在有关断裂,疲劳以及裂纹问题的高阶固体力学发展已经不局限于宏观 (macro-scale) 层面了,或者说宏观固体力学发展已经相对成熟,突破不大。然而从材料微观 (micro-scale) 的细小缺陷开始进行模拟的微观力学 (micro-mechanics) 是发展的一个方向。微观力学结合宏观力学的材料力学模拟就称为多尺度(multi-scale)固体力学,这是将来一个热点问题。
很多我们直觉的想法一旦到了微观领域都改变了,比如尺寸效应。为了得到相应的微观模型参数,实验是不可少的。右图就是在某型号钢材微观拉长实验中,孔洞在拉长之后的变形情况。而材料种类有很多,由此学科诞生的各种实验确定模型参数的工作量是巨大的 (有点偏材料学了)。任何宏观系统的表现形态,都是微观粒子个体行为集成的宏观表现:即宏观系统如何(How)表现,为什么(Why)如此表现,其根本是宏观系统的每一个粒子处于(What)什么微观状态(由量子力学的原理,我们无法考察每个微观粒子如何(How)运动,但对于粒子的关键特征,如什么(What,实际是量子化的Which)能量状态,我们可以用What来刻画)。这一部分可与量子力学的学科范式产生紧密的联系。
多尺度力学方法需要以材料的微观结构信息为基础,目前能够从微观尺度上对材料进行力学分析的方法有第一性原理、分子动力学 (Molecular dynamics, MD)、晶体塑性力学方法等。其中,MD方法是基于原子间相互作用的微观模拟方法,以其能够给出微观结构的动态演化信息从而能够分析大量微观机制而被广泛应用。尽管 MD 方法在时空尺度上存在一定的局限性,但大量研究表明,MD 的模拟结果能够清晰地阐明材料的变形和破坏机制,为跨尺度力学分析奠定重要的物理基础。晶体塑性力学是基于晶体位错滑移理论的一种连续介质力学方法,其可以从底层微结构信息出发,分析材料的宏观力学行为。近年来,以晶体塑性理论为基础的多尺度力学模型随着计算机模拟技术的发展,在结构完整性分析中得到越来越广泛的应用。理机制分析指导结构件的力学性能优化。 现如今,研究各类固体材料力学行为的宏微观理论计算方法越来越丰富,然而,不同尺度下的计算方法所得到的材料力学性质会有一定的差异,如何发展宏微观下多尺度统一的力学方法是一个非常具有挑战性的课题。另一方面,数据技术驱动的人工智能方法发展迅速,这为人们提供了一种全新的数据驱动的(data-driven)力学研究方法。基于微观模拟或试验得到的微观物理信息数据库,采用深度学习的方法进行数据训练,更高效地开发新的力学模型,对于实际工程应用中的结构完整性问题给出快速可靠的分析结果。
非线性耦合 (nonlinear coupled)
在固体力学理论已经成熟的情况下,如何高效实现这些理论也是一个热点。比如非线性耦合问题就出现在很多高级固体力学模型中,具体体现为在实现过程中要求解很多相互耦合的高阶非线性问题。这些求解过程在基于有限元的计算力学很多都是无法实现的或者计算时间太长 (每个高斯积分点都要求解)。因此如何把强耦合 (strongly coupled) 的问题化简为非耦合 (Decoupled) 或者弱耦合 (weakly-coupled) 的问题,使得实现过程相对简单,也是一个热点问题。
非线性力学是非线性科学的一个重要分支,它曾经也将持续对非线性科学的发展起积极的推动作用,多体问题、Stokes波、Riemann问题都是典型的例子,上世纪60年代发现的孤立子和混沌也有其力学背景,这两个事件是非线性科学形成的里程碑。非线性力学,尤其是固体力学,侧重于研究固体物质机械运动中的非线性现象。
非线性问题,即叠加原理不再适用的一大类问题,基于这一原因,原来适用于数学物理中的各类线性方程的方法如:分离变量、积分变换、Green函数等统统失效。目前已发展出摄动法、速度图法、李群变换(包括相似性解)、反演散射法等一系列针对非线性问题的有效解法,但都不具有普适性,只对非线性问题中的少数特例起作用。目前,非线性计算稳定性、谱方法、自由边界问题、有限自由度系统等问题,是非线性问题中亟待解决的若干难点。
非线性问题解法的发展离不开计算技术的发展,符号计算(symbolic computation)和并行计算(parallel computing)将成为非线性问题计算的新范式,而符号计算下的非线性问题系统的描述,其本身就是一个偏序集。由于符号计算消除了有限步之内的数值误差,使其计算过程具有自反性,反对称性与传递性。并行计算下的非线性系统,其描述也是对称破缺的,非线性系统本身引起的非对称性,和剖分并行在处理方法上引入的对称性,为我们认识并解决非线性问题提供了新的视角和方法。
结论
固体力学发展近四百年的历史中范式转换的过程,可以用范畴论中的态射进行刻画,(一个范式内:问题→解决方案的关系是函数;从A范式到B范式之间的映射是函子;而AB范式转换→BC范式转换两过程的比较是自然转换),整个范式转换的过程构成了偏序集的数据结构,它是没有回圈的。在每个范式的科学共同体中,科学家的语言构成了该范式的命名空间,随着范式的转化,命名空间也会有所改变。由于每隔一段时间在学科发展中出现的反常,固体力学的发展会在不同范式之间出现对称破缺,即所谓的不可通约性。当固体力学问题与其他学科发生交叉时,不同范式之间发生超链接。不可通约性在目前固体力学的前沿发展中主要体现在以下两个待解决的问题中——即多尺度问题和非线性问题,由上文所述,多尺度本身就具备良好的偏序结构(尺度上的传递性有序结构),而非线性系统是对称破缺的(物理系统所满足的规律具有某种对称性,但是系统本身不具有这种对称性),对这两个问题的认识将决定未来固体力学学科范式的发展走向。
References
- ↑ Kuhn, Thomas (2012). 科学革命的结构. Translated by 金吾伦; 胡新和 (4th ed.). local page: 北京大学出版社. ISBN 978-7-301-21426-8.
- ↑ 黄欣荣.大数据时代的思维变革[J].重庆理工大学学报(社会科学),2014,28(05):13-18.
- ↑ 钱学森,于景元,戴汝为.一个科学新领域——开放的复杂巨系统及其方法论[J].自然杂志,1990(01):3-10+64.
- ↑ 《大数据时代:生活、工作与思维的大变革》舍恩伯格著,周涛译,浙江:浙江人民出版社,2012,第5页
- ↑ von Mises, R. (1913). "Mechanik der festen Körper im plastisch-deformablen Zustand". Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen. Mathematisch-Physikalische Klasse. 1913 (1): 582–592.
- ↑ Huber, M. T. (1904). "Właściwa praca odkształcenia jako miara wytezenia materiału". Czasopismo Techniczne. Lwów. 22.翻译为 "Specific Work of Strain as a Measure of Material Effort". Archives of Mechanics. 56: 173–190. 2004.
- ↑ See Timoshenko, S. P. (1953). History of Strength of Materials. New York: McGraw-Hill. p. 369. ISBN 9780486611877.
- ↑ 余寿文. 断裂力学的历史发展与思考[C]. 中国力学学会力学史与方法论专业委员会.第七届全国力学史与方法论学术研讨会力学与实践专刊.中国力学学会力学史与方法论专业委员会:中国力学学会,2015:106-110.
- ↑ 余寿文. 断裂力学的历史发展与思考[C]. 中国力学学会力学史与方法论专业委员会.第七届全国力学史与方法论学术研讨会力学与实践专刊.中国力学学会力学史与方法论专业委员会:中国力学学会,2015:106-110.
- ↑ 康颖安.断裂力学的发展与研究现状[J].湖南工程学院学报(自然科学版),2006(01):39-42.
- ↑ Griffith, Alan Arnold. "VI. The phenomena of rupture and flow in solids." Philosophical transactions of the royal society of london. Series A, containing papers of a mathematical or physical character 221.582-593 (1921): 163-198.
- ↑ 余寿文. 现代固体力学研究范畴的讨论——固体力学史与方法论的注记之二[C]. 中国力学学会力学史与方法论专业委员会.第三届全国力学史与方法论学术研讨会论文集.中国力学学会力学史与方法论专业委员会:中国力学学会力学史与方法论专业委员会,2007:32-38.
- ↑ 严锐.复合材料力学综述[J].工程与建设,2017,31(02):159-161


























![{\displaystyle \sigma _{v}^{2}={\tfrac {1}{2}}[(\sigma _{11}-\sigma _{22})^{2}+(\sigma _{22}-\sigma _{33})^{2}+(\sigma _{11}-\sigma _{33})^{2}+6(\sigma _{23}^{2}+\sigma _{31}^{2}+\sigma _{12}^{2})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/918b083c9c0c4f9cb190d778ecfdc3fd9eb6e4f9)