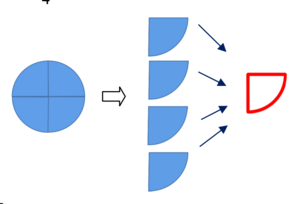
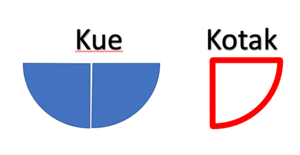
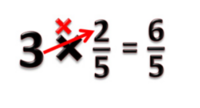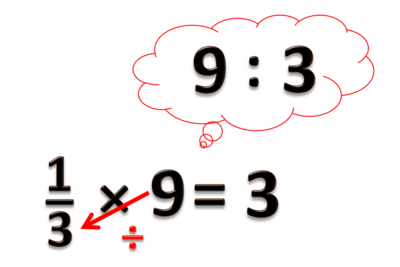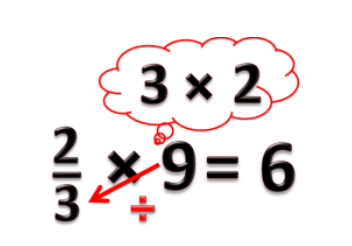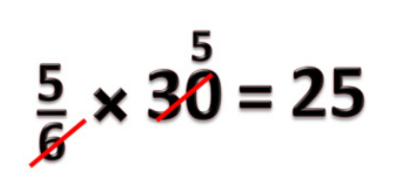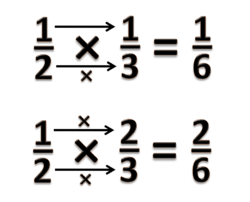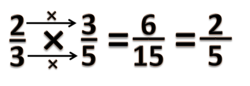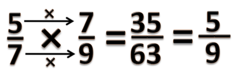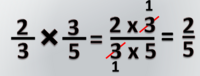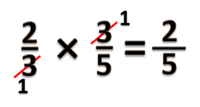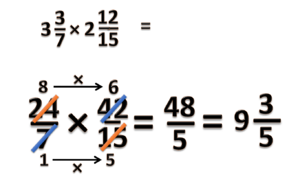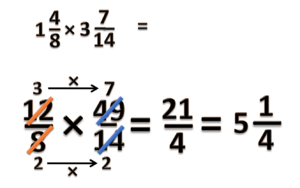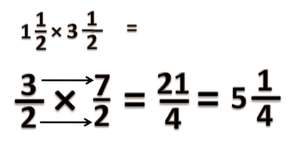Gaber pecahan 2
Perkalian Pecahan
Pembahasan perkalian pecahan akan kita bagi dalam 4 bagian
- Perkalian bilangan bulat dengan pecahan
- Perkalian pecahan dengan bilangan bulat
- Perkalian pecahan dengan pecahan
- Perkalian pecahan majemuk
Bilangan Bulat x bilangan Pecahan
- Perkalian bilangan pecahan menggunakan dasar konsep perkalian bilangan bulat yang sudah dipelajari sebelumnya.
- Dalam perkalian bilangan bulat kita tentu masih ingat bahwa 3 x 2 artinya 3 kotak isi 2, yaitu konkretnya ada 3 kotak yang masing-masing isinya 2 benda.
- Jadi hasilnya (abstrak) adalah 3 x 2 = 3▢2 = = 2 + 2 + 2 = 6.
- Sekarang bagaimana dengan 2 x ?
- 2 x artinya 2 kotak isi
- Konkretnya ada 2 kotak yang masing-masing berisi benda.
Jadi, abstraknya adalah
- 2 x = 2▢ = + = = 1
Begitu pula
- 3 x = 3▢ = + + =
Kongkretnya digambarkan sebagai 3 kotak masing-masing berisi
Lakukan kegiatan eksplorasi perkalian bilangan bulat dengan pecahan seperti di atas dengan berbagai soal sehingga siswa menemukan pola bagaimana mendapatkan hasilnya dengan cepat, yaitu dengan mengalikan bilangan bulat dengan pembilang.
- Contohnya
- 3 x = 3▢ = + + = =
- Cara cepat
Video berikut menunjukan beberapa contoh perkalian bilangan bulat dengan bilangan pecahan.
{{#ev:YouTube |id= NZqqy1RcQ30 |width=640 |height=400 }}
Bilangan Pecahan x Bilangan Bulat
- Bagaimana dengan perkalian bilangan pecahan dengan bilangan bulat seperti x 6 ?
- x 6 artinya kotak isi 6.
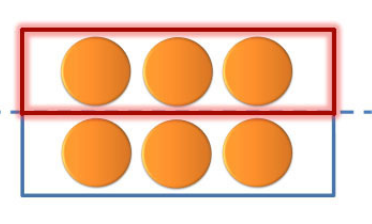
- Jadi konkretnya ada 6 kue dalam suatu kotak lalu kita bagi kotak tersebut menjadi 2 bagian yang sama besar (sehingga banyaknya kue dalam tiap bagian sama). lalu kita hitung berapa isi 1 bagiannya itu.
- Hasilnya adalah 3
- Jadi x 6 = ▢6 = 3
- Sekarang bagaimana dengan x 6 = ?
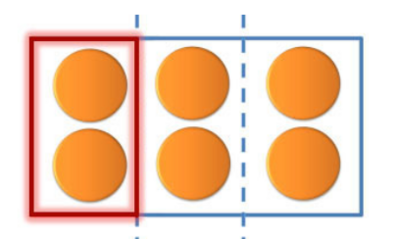
- x 6 artinya kotak isi 6, jadi konkretnya ada 6 kue dalam suatu kotak lalu kita bagi kotak tersebut menjadi 3 bagian yang sama besar (sehingga banyaknya kue dalam tiap bagian sama). Lalu kita hitung berapa isi satu bagian kotak itu?
- Hasilnya adalah 2
- Jadi x 6 = ▢6 = 2
- Bagaimana dengan x 9 = ?
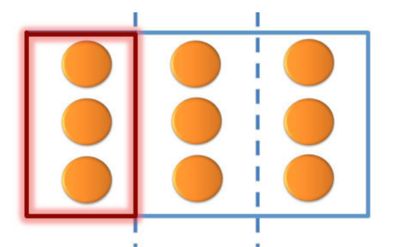
- x 9 artinya kotak isi 9, jadi konkretnya ada 9 kue dalam suatu kotak lalu kita bagi kotak tersebut menjadi 3 bagian yang sama besar (sehingga banyaknya kue dalam tiap bagian sama). Lalu kita hitung berapa isi satu bagian kotak itu?
- Hasilnya adalah 3
- Jadi x 9 = ▢9 = 3
Perhatikan hasil-hasil yang kita peroleh
- x 6 hasilnya sama dengan membayangkan 6÷2 yaitu 3
- x 6 hasilnya sama dengan membayangkan 6÷3 yaitu 2
- x 9 hasilnya sama dengan membayangkan 9÷3 yaitu 3
Kesimpulan apa yang kita peroleh?
Kita lihat bahwa perkalian pecahan dengan bilangan bulat sama dengan pembagian bilangan bulat itu dengan penyebut.
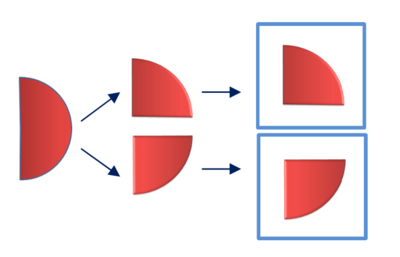
- Bagaimana dengan x 9 = ?
- x 9 artinya kotak isi 9, jadi konkretnya ada 9 benda dalam suatu kotak lalu kita bagi kotak tersebut menjadi 3 bagian yang sama besar (sehingga banyaknya kue dalam tiap bagian sama). Lalu kita hitung berapa isi dua bagian kotak itu?
- Hasilnya adalah 2 x 3 = 6 benda
Hasilnya dapat digambarkan sebagai berikut. Hasilnya adalah 6 kue yang ada dalam daerah yang diarsir.
Berikut ini beberapa contoh perkalian pecahan dengan bilangan bulat
- a) x 12 = ?
- x 12 artinya kotak isi 12, jadi konkretnya ada 12 benda dalam suatu kotak lalu kita bagi kotak tersebut menjadi 4 bagian yang sama besar (sehingga banyaknya kue dalam tiap bagian sama). Lalu kita hitung berapa isi tiga bagian kotak itu?
- Hasilnya adalah 3 x 3 = 9 benda
- b) x 30 = ?
- x 30 artinya kotak isi 30, jadi konkretnya ada 30 benda dalam suatu kotak lalu kita bagi kotak tersebut menjadi 6 bagian yang sama besar (sehingga banyaknya kue dalam tiap bagian sama). Lalu kita hitung berapa isi lima bagian kotak itu?
- Hasilnya adalah 5 x 5 = 25 benda
x 30 = 25
- c) x 49 = ?
- x 49 artinya kotak isi 49, jadi konkretnya ada 49 benda dalam suatu kotak lalu kita bagi kotak tersebut menjadi 7 bagian yang sama besar (sehingga banyaknya kue dalam tiap bagian sama). Lalu kita hitung berapa isi lima bagian kotak itu?
- Hasilnya adalah 7x 5 =35 benda
x 49 = 35
- d) x 18 = ?
- x 18 artinya kotak isi 18, jadi konkretnya ada 18 benda dalam suatu kotak lalu kita bagi kotak tersebut menjadi 9 bagian yang sama besar (sehingga banyaknya kue dalam tiap bagian sama). Lalu kita hitung berapa isi tujuh bagian kotak itu?
- Hasilnya adalah 2x7 = 14 benda
Video berikut menunjukan beberapa contoh perkalian bilangan pecahan dengan bilangan bulat.
{{#ev:YouTube
|id= M9OCkcDBPfc
|width=640
|height=400
}}
Pecahan x Pecahan
Pada bab ini kita akan belajar tentang perkalian pecahan biasa dengan pecahan biasa, seperti
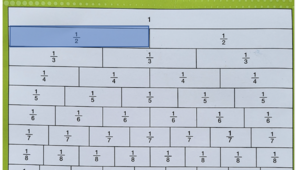
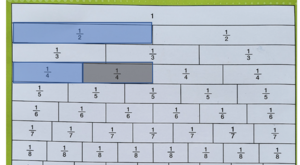
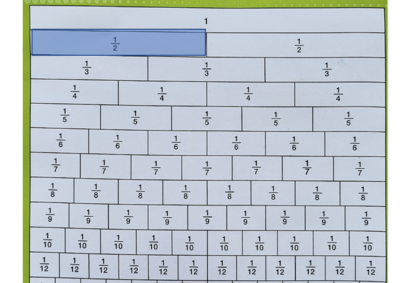
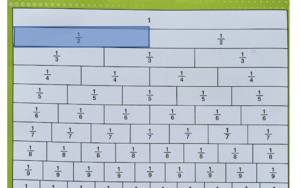
Kita akan gunakan papan pecahan sebagai alat bantu.
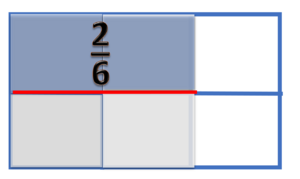
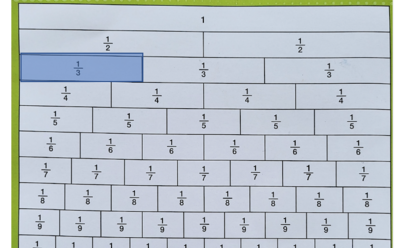
Misalkan kita akan menghitung ×
Ini adalah pecahan
artinya kotak isinya
- Jadi disini kotak kita bagi menjadi dua bagian yang sama besar.
- Kita cari dipapan pecahan, pecahan mana yang besarnya tetapi terbagi atas dua bagian.
- Jawabnya adalah pecahan
- Jadi kita lihat bahwa kalau dibagi 2, hasilnya adalah
- Dengan demikian =
Perhatikan beberapa contoh berikut
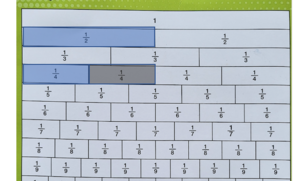
- a)
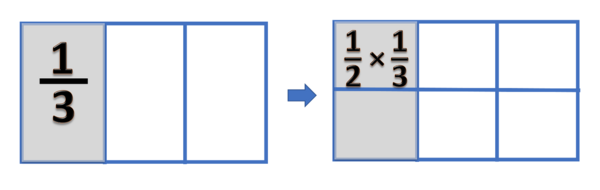
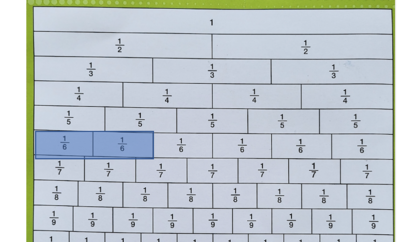
- Pertama kita buat dulu pecahan
- Kemudian pecahan tersebut dibagi menjadi dua bagian yang sama besar.
- Salah satu bagian ini nilainya adalah
- Kalau kita perhatikan pada gambar diatas adalah nilai satu bagian dari satu kelompok yang terdiri dari 6 bagian yang sama besar. Ini adalah definisi
- Sehingga bisa disimpulkan bahwa =
- b)
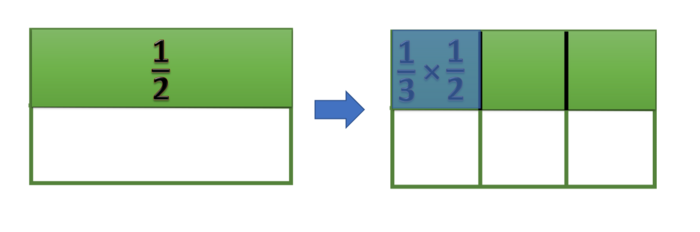
- Pertama kita buat dulu pecahan
- Kemudian pecahan tersebut dibagi menjadi tiga bagian yang sama besar.
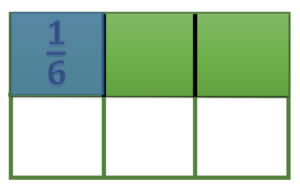
- Salah satu bagian ini nilainya adalah
- Kalau kita perhatikan pada gambar diatas adalah nilai satu bagian dari satu kelompok yang terdiri dari 6 bagian yang sama besar. Ini adalah definisi
- Sehingga bisa disimpulkan bahwa =
- c)
- Pertama kita buat dulu pecahan
- Kemudian pecahan tersebut dibagi menjadi dua bagian yang sama besar.
- Salah satu bagian ini nilainya adalah
- Kalau kita perhatikan pada gambar diatas adalah nilai dua bagian dari satu kelompok yang terdiri dari 6 bagian yang sama besar. Ini adalah definisi
- Sehingga bisa disimpulkan bahwa =
Lakukan eksplorasi ini berulang-ulang, sampai siswa melihat pola bahwa pada perkalian pecahan dengan pecahan, maka hasilnya diperoleh dengan mengalikan pembilang dengan pembilang dan penyebut dengan penyebut.
Perhatikan contoh beberapa perkalian pecahan dibawah ini
- a) = = =
- b) = = =
Cara coret:
Ada kalanya dalam perkalian pecahan kita bisa lakukan cara cepat yaitu dengan membagi pembilang dan penyebut dengan bilangan tertentu sebelum mereka dikalikan.
Perhatikan contoh berikut
- a)
- Langkah pertama adalah mengalikan pembilang dengan pembilang dan penyebut dengan penyebut
- =
- Langkah kedua adalah membagi pembilang dan penyebut dengan 3.
- Pembilang 3 ÷ 3 = 1
- Penyebut 3 ÷ 3 = 1
- Langkah ketiga adalah kalikan pembilang dengan pembilang dan penyebut dengan penyebut
- Pembilang 2 x 1 = 2
- Penyebut 1 x 5 = 5
- Hasilnya adalah
Kalau sudah mahir kita bisa coret diawal seperti pada gambar ini.
- Pembilang 2 x 1 = 2
- Penyebut 1 x 5 = 5
- Hasilnya
- b)
- Langkah pertama adalah mengalikan pembilang dengan pembilang dan penyebut dengan penyebut
- =
- Langkah kedua adalah membagi pembilang dan penyebut dengan 7.
- Pembilang 7÷7 = 1
- Penyebut 7÷7 = 1
- Langkah ketiga adalah kalikan pembilang dengan pembilang dan penyebut dengan penyebut
- Pembilang 5 x 1 = 5
- Penyebut 1 x 9 = 9
- Hasilnya adalah
Kalau sudah mahir kita bisa coret diawal seperti pada gambar ini.
- Pembilang 5 x 1 = 5
- Penyebut 1 x 9 = 9
- Hasilnya
- c)
Kita bisa selesaikan soal ini dengan mengalikan pembilang dengan pembilang dan penyebut dengan penyebut. Kemudian kita sederhanakan seperti ditunjukan pada gambar ini.
Atau kita melakukan penyederhanaan diawal pembilang dan penyebut dibagi dengan bilangan yang sama.
- 16 ÷ 4 = 4 (pembilang) dan 4 ÷ 4 = 1 (penyebut)
- 15 ÷ 3 = 5 (penyebut) dan 9:3 = 3 (pembilang)
Kemudian mengalikan pembilang dengan pembilang dan penyebut dengan penyebut
- Pembilang = 4 x 3 = 12
- Penyebut = 5 x 1 = 5
Video berikut ini beberapa contoh perkalian pecahan dengan pecahan
{{#ev:YouTube
|id= xDjEDKLGLys
|width=640
|height=400
}}
- Aktivitas 14
Tujuan: siswa mengerjakan secara cepat soal-soal mengenai perkalian pecahan
Mengerjakan Latihan 24-26 dari buku Pecahan (buku 4)
Pecahan Majemuk x Pecahan Majemuk
Pada perkalian pecahan majemuk, kita harus mengubah dulu pecahan majemuk ini menjadi pecahan biasa. Setelah itu kita bisa lakukan perkalian pecahan seperti yang sudah dipelajari sebelumnya.
Perhatikan contoh berikut
- a) =
Hasil perhitungan diberikan pada gambar dibawah ini
- b) =
Hasil perhitungan diberikan pada gambar dibawah ini
- c) =
Hasil perhitungan dapat dilihat pada gambar dibawah ini
Pada soal diatas kita bisa juga menyederhanakan pecahan lebih awal lagi
Hasilnya adalah
Video berikut ini memberikan beberapa variasi soal perkalian pecahan majemuk
{{#ev:YouTube |id= Z9I-h-4lcRU |width=640 |height=400 }}
- Aktivitas 15
Tujuan: siswa mengerjakan secara cepat soal-soal mengenai perkalian pecahan majemuk
Mengerjakan Latihan 27 dari buku Pecahan (buku 4)
Perkalian 3 Pecahan
Pada perkalian 3 pecahan kita bisa lakukan dengan sistem coret.
Untuk lebih jelasnya lihat video berikut ini.
{{#ev:YouTube
|id= 3v2nL6veuZ0
|width=640
|height=400
}}
- Aktivitas 16
Tujuan: siswa mengerjakan secara cepat soal-soal mengenai perkalian pecahan majemuk
Mengerjakan Latihan 28 dari buku Pecahan (buku 4)
Pembagian Pecahan
Pembahasan pembagian pecahan akan kita bagi dalam 4 bagian
- Pembagian bilangan bulat dengan pecahan
- Pembagian pecahan dengan bilangan bulat
- Pembagian pecahan dengan pecahan
- Pembagian pecahan majemuk
Bilangan Pecahan ÷ Bilangan Bulat
- Pembagian pecahan menggunakan dasar konsep pembagian yang sudah dipelajari sebelumnya.
- Dalam pembagian kita tentu masih ingat bahwa 6 ÷ 2 artinya saya punya 6 benda hendak dimasukan dalam 2 kotak, berapa yang diterima tiap kotak.
- Kita sudah tahu bahwa jawabnya adalah 3 benda.
- Bagaimana dengan pembagian bilangan pecahan dengan bilangan bulat seperti ÷ 2 ?
- ÷ 2 artinya kue hendak dimasukan dalam 2 kotak. Berapa isi masing-masing kotak agar pembagian ini adil dan merata.
Yang kita perlu lakukan adalah membagi dua kue itu. Kemudian memasukan tiap bagian ke dalam kotak. Kita lihat tiap kotak akan menerima masing-masing kue.
Dengan demikian ÷ 2 =
- Sekarang bagaimana dengan : 2 = ?
Kita bisa gunakan papan pecahan.
Ini pecahan
Cari di papan pecahan, pecahan yang nilainya tapi terbagi 2.
Jawabnya adalah pada gambar ini
Disini terlihat bahwa
- Bagaimana dengan ÷ 5 = ?
Kita bisa gunakan papan pecahan.
Ini pecahan
Cari di papan pecahan, pecahan yang nilainya tapi terbagi 5.
Jawabnya adalah pada gambar ini
Disini terlihat bahwa
Perhatikan hasil-hasil yang kita peroleh dibawah ini
- ÷ 6, kita membayangkan 1/2 kue dipotong-potong jadi 6 bagian yang sama hasilnya yaitu
- ÷ 4, kita membayangkan 1/3 kue dipotong-potong jadi 4 bagian yang sama hasilnya yaitu
- ÷ 7, kita membayangkan 1/5 kue dipotong-potong menjadi 7 bagian yang sama hasilnya yaitu
Video berikut menunjukan beberapa contoh perkalian bilangan pecahan dengan bilangan bulat.
{{#ev:YouTube |id= DBSXhkjXA7o |width=640 |height=400 }}
Bilangan Bulat ÷ Bilangan Pecahan
- Kalimat perkalian 2 x 3 = 6, artinya jika ada 2 kotak masing-masing kotak isi 3 benda maka jumlah seluruh benda dalam kotak-kotak itu adalah 6 benda.
- Dari perkalian 2 x 3 = 6, maka arti pembagian 6:2 = 3 adalah kita punya 6 benda hendak dibagikan dalam 2 kotak, maka isi tiap kotak adalah 3 benda.
- Dari perkalian 2 x 3 = 6, maka arti pembagian 6:3 = 2 adalah kita punya 6 benda hendak dimasukan dalam kotak, setiap kotak hanya bisa menampung 3 benda, maka jumlah kotak yang bisa menerima 6 benda ini ada 2 kotak.
Disini kita lihat ada 2 arti pembagian. Pembagian pertama yang sering kita pakai adalah menanyakan isi kotak. Sedangkan pembagian kedua adalah menanyakan banyak kotak.
Untuk perkalian bilangan bulat x bilangan pecahan, kita akan gunakan arti pembagian kedua.
Contoh: 1÷ = ? Untuk melihat konkretnya ada baiknya kita ambil wadah air 1 liter dan wadah air 1/2 liter. Air dituang dari wadah 1 liter ke wadah 1/2 liter... kita lihat bahwa kita membutuhkan 2 wadah yang 1/2 liter.
Jadi 1÷ = 2
- Bagaimana dengan pembagian 1 ÷ ?
- Saya punya kue hendak dimasukan dalam kotak dengan kapasitas atau ukuran , berapa banyak potong kue dapat dimasukan dalam kotak tersebut?
Gambar dibawah ini menggambarkan situasi ketika 1 potong kue sudah masuk kotak pertama.
Ini gambar situasi ketika 2 potong kue sudah masuk kotak kedua.
Jadi jumlah kotak yang dibutuhkan adalah 2 kotak.
Sekarang kita akan hitung 1 ÷
- Pada gambar diatas kita punya 1 kue, hendak kita masukan dalam beberapa kotak dengan kapasitas atau ukuran .
- Kue kita bagi menjadi potongan agar bisa masuk kotak.
- Kita lihat bahwa banyak kotak adalah 4 buah.
Jadi
- 1 ÷ = 4
Bisa juga kita gunakan wadah 1 liter dan wadah 1/4 liter. Air dalam wadah 1 liter kita tuangkan dalam wadah 1/4 liter dan kita bisa lihat bahwa untuk ini dibutuhkan 4 wadah. Jadi
1 ÷ = 4
Dengan cara yang sama kita bisa dapatkan bahwa
- 1 ÷ = 3
- 1 ÷ = 6
- 1 ÷ = 10
Pola apa yang Anda lihat?
- Bagaimana kalau 2 ÷ = ?
- Karena
- 1 ÷ = 2
- maka
- 2 ÷ = 2 x 2 = 4
Dengan cara yang sama kita bisa peroleh
- 2 ÷ = 2 x 3 = 6
- 2 ÷ = 2 x 4 = 8
- 2 ÷ = 2 x 6 = 12
- 2 ÷ = 2 x 10 = 20
Dan dengan pola yang sama kita bisa peroleh
- 5 ÷ = 5 x 3 = 15
- 9 ÷ = 9 x 4 = 36
- 12 ÷ = 12 x 6 = 72
- 25 ÷ = 25 x 10 = 250
Jadi resep untuk menghitung perbagian bilangan bulat dengan bilangan pecahan seperti 25 ÷ adalah dengan membayangkan 1 kali÷ . Kemudian hasilnya ini dikalikan 25. Hasilnya adalah 250.
Video berikut menunjukan berbagai contoh pembagian bilangan bulat dengan pecahan.
{{#ev:YouTube |id= RbJ0IYVfnss |width=640 |height=400 }}
Pecahan ÷ Pecahan
Pada bagian ini kita akan belajar tentang pembagian pecahan biasa dengan pecahan biasa, seperti
Misalkan kita akan menghitung ÷
artinya ada kue berukuran hendak dimasukan dalam kotak berukuran , ada berapa banyak kotak dibutuhkan?
Kue berukuran tidak bisa masuk kedalam kotak berukuran . Karena itu maka kue harus dipotong menjadi beberapa potongan kue berukuran .
Kita lihat pada gambar bahwa kue bisa dipotong menjadi 2 kue berukuran .
Kue yang sudah dipotong ini dimasukan satu persatu ke dalam kotak .
Banyak kotak yang dibutuhkan adalah 2 buah.
- Dengan demikian = 2
Kita bisa juga lakukan ini dengan wadah 1/2 liter air dan wadah 1/4 liter air. Kita masukan air dari wadah 1/2 liter ke wadah 1/4 liter. Kita lihat bahwa kita butuh 2 wadah. Jadi
= 2
Sekarang kita gunakan papan pecahan untuk menjelaskan soal diatas.
Ini adalah pecahan
artinya ada batang hendak dimasukan dalam kotak , ada berapa buah kotak dibutuhkan.
Pecahan terlalu besar untuk masuk kotak . Karena itu maka pecahan itu harus dipotong menjadi beberapa potongan pecahan .
Kita lihat pada gambar bahwa pecahan bisa dipotong menjadi 2 buah pecahan .
Potongan pecahan ini \kemudian dimasukan satu persatu ke dalam kotak .
Banyak kotak yang dibutuhkan adalah 2 buah.
- Dengan demikian = 2
Perhatikan beberapa contoh berikut
- a)
- Arti adalah kita mempunyai pecahan
hendak dimasukan dalam kotak berukuran , tentunya pecahan itu harus dipotong-potong. Ada berapa kotak dibutuhkan?
- Cari di papan pecahan, pecahan
- Tempatkan pecahan ini ke dalam deretan pecahan . Kita lihat
ada 4 pecahan yang nilainya . Dengan kata lain ada 4 kotak dibutuhkan untuk menampung .